设X,Y相互独立且都服从分布N(0,4),则( ).
题目
设X,Y相互独立且都服从分布N(0,4),则( ).
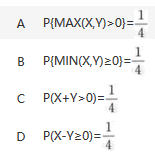
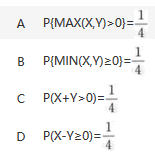
相似考题
更多“设X,Y相互独立且都服从分布N(0,4),则( ). ”相关问题
-
第1题:
设随机变量X和Y都服从正态分布,则().A.X+Y一定服从正态分布
B.(X,Y)一定服从二维正态分布
C.X与Y不相关,则X,Y相互独立
D.若X与Y相互独立,则X-Y服从正态分布答案:D解析:若X,Y独立且都服从正态分布,则X,Y的任意线性组合也服从正态分布,选(D). -
第2题:
设两个相互独立的随机变量X和Y分别服从正态分布N(0,1)和N(1,1),则
 答案:B解析:【简解】首先应看到,X+Y和X-Y均为一维正态分布的随机变量.其次要看到,如果z~N(μ,σ^2),则
答案:B解析:【简解】首先应看到,X+Y和X-Y均为一维正态分布的随机变量.其次要看到,如果z~N(μ,σ^2),则 ,反之,如果
,反之,如果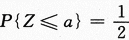 ,则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化,更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解,就更复杂化了.
,则必有a=μ.因为正态分布的概率密度有对称性.有考生在求解过程中将X+Y和X-Y都进行标准化,更有考生把X+Y和X-Y都看成二维正态随机变量的函数来求解,就更复杂化了.
-
第3题:
设X,Y相互独立且都服从标准正态分布,则E|X-Y|=_______,D|X-Y|=_______.答案:解析: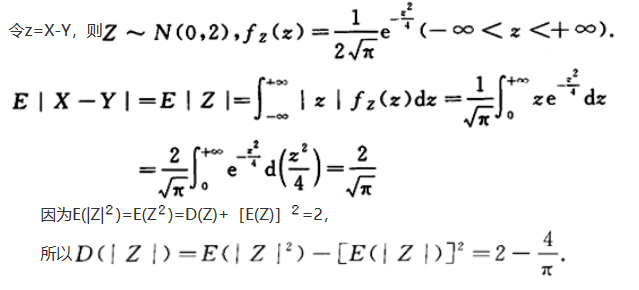
-
第4题:
设总体X,Y相互独立且都服从N(μ,σ^2)分布,(X1,X2,…,Xn)与(Y1,Y1,…,yn)分别为来自总体X,Y的简单随机样本,证明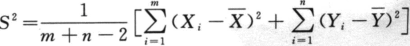 :为参数σ^2的无偏估计量,答案:解析:
:为参数σ^2的无偏估计量,答案:解析: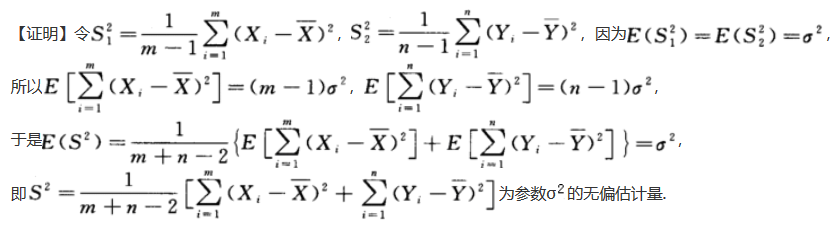
-
第5题:
设X,Y相互独立且都服从(0,2)上的均匀分布,令Z=min{X,Y},则P(0答案:解析:由X,Y在(0,2)上服从均匀分布得
因为x,Y相互独立,所以
Fz(z)=P(Z≤z)=1-P(Z>z)=1-P(min{X,Y)}>z)=1-P(X>z,Y>z)
=1-P(X>z)P(Y>z)=1=【1-P(X≤z)】【1-P(Y≤z)】
=1-【1-Fx(z)】【1-FY(z)】,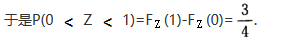
第6题:
设随机变量X,Y相互独立,且X~N(0,4),Y的分布律为Y~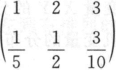 .则P(X-1-2Y≤4)=_______.答案:1、0.46587解析:p(X+2Y≤4)=P(Y=1)P(X≤4-2Y|Y=1)+P(Y=2)P(X≤4-2Y|Y=2)+P(Y=3)P(X≤4-2Y|Y=3)
.则P(X-1-2Y≤4)=_______.答案:1、0.46587解析:p(X+2Y≤4)=P(Y=1)P(X≤4-2Y|Y=1)+P(Y=2)P(X≤4-2Y|Y=2)+P(Y=3)P(X≤4-2Y|Y=3)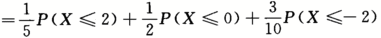

第7题:
设随机变量X,Y相互独立,且X~N(μ,σ2),Y在[a,b]区间上服从均匀分布,则D(X-2Y)=()。
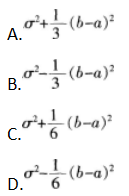 答案:A解析:
答案:A解析: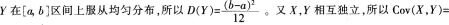
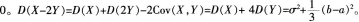
第8题:
设随机变量X与Y相互独立且都服从区间[0,1]上的均匀分布,则下列随机变量中服从均匀分布的有()。
- A、X2
- B、X+Y
- C、(X,Y)
- D、X-Y
正确答案:C第9题:
X,Y相互独立,且都服[0,1]上的均匀分布,则服从均匀分布的是().
- A、(X,Y)
- B、XY
- C、X+Y
- D、X-Y
正确答案:A第10题:
若随机变量X~N(0,4),Y~N(-1,5),且X与Y相互独立。设Z=X+Y-3,则Z~()。
正确答案:N(-4,9)第11题:
设X,Y相互独立,且都服从标准正态分布N(0,1),令Z=X2+Y2则Z服从的分布是().
- A、N(0,2)分布
- B、单位圆上的均匀分布
- C、参数为1的瑞利分布
- D、N(0,1)分布
正确答案:C第12题:
单选题若随机向量(X,Y)服从二维正态分布,则( )。[2018年10月真题]Ⅰ.X,Y一定相互独立Ⅱ.若ρXY=0,则X,Y一定相互独立Ⅲ.X和Y都服从一维正态分布Ⅳ.若X,Y相互独立,则Cov(X,Y)=0AⅠ、Ⅲ
BⅠ、Ⅲ、Ⅳ
CⅡ、Ⅲ、Ⅳ
DⅡ、Ⅳ
正确答案: B解析:
Ⅰ、Ⅱ项,对于二维正态随机变量(X,Y),X和Y相互独立的充要条件是参数ρXY=0。Ⅲ项,若随机向量(X,Y)服从二维正态分布,则X和Y都服从一维正态分布,但反之不一定。Ⅳ项,若X,Y相互独立,E(XY)=E(X)E(Y),则Cov(X,Y)=E(XY)-E(X)E(Y)=0。第13题:
设(X,Y)服从二维正态分布,则下列说法不正确的是().
A.X,Y一定相互独立
B.X,y的任意线性组合l1X+l2y(l1,l2不全为零)服从正态分布
C.X,y都服从正态分布
D.ρ=0时X,y相互独立答案:A解析:因为(X,Y)服从二维正态分布,所以(B),(C),(D)都是正确的,只有当ρ=0时,X,Y才相互独立,所以选(A).第14题:
设随机变量X,Y都是正态变量,且X,Y不相关,则( ).
A.X,Y一定相互独立
B.(X,Y)一定服从二维正态分布
C.X,y不一定相互独立
D.X+y服从一维正态分布
答案:C解析:只有当(X,Y)服从二维正态分布时,X,Y独立才与X,Y不相关等价,由X,Y仅仅是正态变量且不相关不能推出X,Y相互独立,(A)不对;若X,Y都服从正态分布且相互独立,则(X,Y)服从二维正态分布,但X,Y不一定相互独立,(B)不对;当X,Y相互独立时才能推出X,Y服从一维正态分布,(D)不对,故选(C)第15题:
设二维随机变量(X,Y)服从二维正态分布,且X~N(1,3^2),Y~N(0,4^2),且X,Y的相
关系数为- ,又设Z=
,又设Z=
(1)求E(Z),D(Z);(2)求 ;(3)X,Z是否相互独立?为什么?答案:解析:【解】(1)
;(3)X,Z是否相互独立?为什么?答案:解析:【解】(1)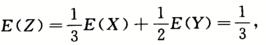

(2)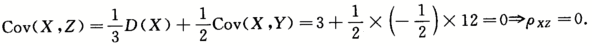
(3)因为(X,Y)服从二维正态分布,所以Z服从正态分布,同时X也服从正态分布,又X,
Z不相关,所以X,Z相互独立.第16题:
设总体X,Y相互独立且服从N(0,9)分布,(X1,…,X9)与(Y1,…,Y9)分别为来自总体X,Y的简单随机样本,则U=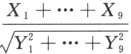 ~_______.答案:1、t(9)解析:
~_______.答案:1、t(9)解析:
第17题:
设随机变量X,Y相互独立且都服从二项分布B(n,p),则P{min(X,Y)=0}=_______.答案:解析:令A=(X=0),B=(Y=0),则P{min(X,Y)=0)=P(A+B)=P(A)+P(B)-P(AB)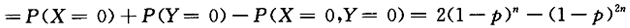
第18题:
设U,~N(μ,1),V~χ^2(n),且U,V相互独立,则T=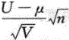 服从_______分布.答案:1、t(n)解析:由U~N(μ,1),得
服从_______分布.答案:1、t(n)解析:由U~N(μ,1),得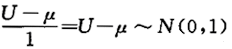 ,又U,V相互独立,则.
,又U,V相互独立,则.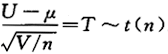
第19题:
设随机变量X和Y相互独立,都服从正态分布N(0,1/2),则Y−X的方差为()。
- A、1-1/π
- B、1-2/π
- C、1
- D、2
- E、4
正确答案:B第20题:
设(X,Y)服从二维正态分布,则cov(X,Y)=0是X与Y相互独立的()条件。
正确答案:充要第21题:
若随机变量X与Y相互独立,且X服从N(1,9),Y服从N(2,6),则X+Y服从()分布。
正确答案:N(3,25)第22题:
设随机变量X,Y相互独立,且均服从[0,1]上的均匀分布,则服从均匀分布的是()。
- A、XY
- B、(X,Y)
- C、X—Y
- D、X+Y
正确答案:B第23题:
单选题若随机向量(X,Y)服从二维正态分布,则( )。Ⅰ.X,Y一定相互独立Ⅱ.若ρXY=0,则X,Y一定相互独立Ⅲ.X和Y都服从一维正态分布Ⅳ.若X,Y相互独立,则Cov(X,Y)=0AⅠ、Ⅲ
BⅠ、Ⅲ、Ⅳ
CⅡ、Ⅲ、Ⅳ
DⅡ、Ⅳ
正确答案: A解析:
Ⅰ、Ⅱ项,对于二维正态随机变量(X,Y),X和Y相互独立的充要条件是参数ρXY=0。Ⅲ项,若随机向量(X,Y)服从二维正态分布,则X和Y都服从一维正态分布,但反之不一定。Ⅳ项,若X,Y相互独立,E(XY)=E(X)E(Y),则Cov(X,Y)=E(XY)-E(X)E(Y)=0。
