设f（x）有连续导数，则下列关系式中正确的是：

题目

相似考题

1.设函数f(x）=e5x，则f(x)的n阶导数f(n)(x)=____．

2.设随机变量X～b(n，P)，则下列关系式正确的有( )。

3.设函数f（x）在区间[a，b]上连续，则下列结论中哪个不正确？

4.设F(x)=P(X≤x)是连续型随机变量X的分布函数，则下列结论中不正确的是A、F(x)是不增函数B、0≤F(x)≤1C、F(x)是右连续的D、F(-∞)=0,F(+∞)=1

更多“设f（x）有连续导数，则下列关系式中正确的是： ”相关问题

第1题：

设函数f（x）连续，则下列函数中必为偶函数的是（）

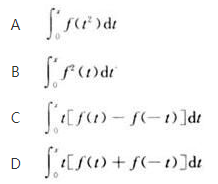答案：D
解析：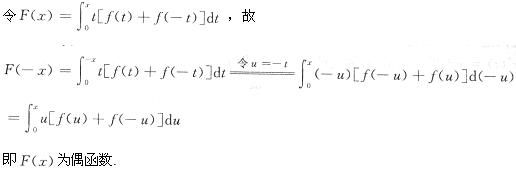
第2题：

对于二元函数z=f(x,y)，下列有关偏导数与全微分关系的命题中，哪一个是正确的？
A.偏导数不连续，则全微分必不存在
B.偏导数连续，则全微分必存在
C.全微分存在，则偏导数必连续
D.全微分存在，而偏导数不一定存在

答案：B
解析：
提示:偏导数连续是函数可微的充分条件。
第3题：

设函数f(μ，ν)具有二阶连续偏导数，z=f(x，xy)，则=________.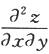

答案：
解析：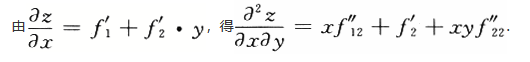
第4题：

设f(x)有连续的导数，f(0)=0,

答案：B
解析：
第5题：

设f(x)具有二阶导数，y=f(x2),则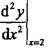的值为()。

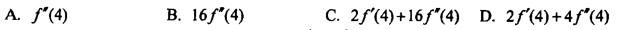答案：C
解析：
正确答案是C。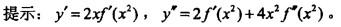
第6题：

设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？
- A、f″（x）+f′（x）=0
- B、f″（x）-f′（x）=0
- C、f″（x）+f（x）=0
- D、f″（x）-f（x）=0
正确答案:C
第7题：

下列结论正确的是（）.
- A、x=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
- B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
- C、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
- D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件
正确答案:D
第8题：

填空题
设z＝f（x，xy）二阶偏导数连续，则∂2z/∂x∂y＝____。

正确答案： f₂′+xf₁₂″+xyf₂₂″
解析：
∂z/∂x＝f₁′＋yf₂′，∂²z/（∂x∂y）＝f₁₁″·0＋xf₁₂″＋f₂′＋yf₂₂″·x＝xf₁₂″＋f₂′＋xyf₂₂″
第9题：

单选题
（2013）设f（x）有连续导数，则下列关系式中正确的是：（）
A
∫f（x）dx=f（x）
B
［∫f（x）dx］′=f（x）
C
∫f′（x）dx=f（x）dx
D
［∫f（x）dx］′=f（x）=c

正确答案： B
解析：暂无解析
第10题：

单选题
对于二元函数z=f（x，y），下列有关偏导数与全微分关系中正确的命题是（）。
A
偏导数存在，则全微分存在
B
偏导数连续，则全微分必存在
C
全微分存在，则偏导数必连续
D
全微分存在，而偏导数不一定存在

正确答案： B
解析：暂无解析
第11题：

单选题
对于二元函数z=f（x，y），下列有关偏导数与全微分关系的命题中，哪一个是正确的（）？
A
偏导数不连续，则全微分必不存在
B
偏导数连续，则全微分必存在
C
全微分存在，则偏导数必连续
D
全微分存在，而偏导数不一定存在

正确答案： C
解析：偏导数连续是函数可微的充分条件。
第12题：

单选题
下列结论正确的是（）.
A
x=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
B
z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
C
z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
D
z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件

正确答案： B
解析：暂无解析
第13题：

设函数f(x)在区间[a,b]上连续，则下列结论中哪个不正确？

D.f(x)在[a,b]上是可积的

答案：A
解析：
提示:f(x)在[a,b]上连续，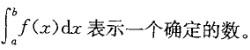
第14题：

函数f(x)在区间[a，b]上连续，且x∈[a，b]，则下列导数为零的是（　　）．

答案：B
解析：
第15题：

设函数f(x)具有2阶连续导数，若曲线y=f(x)过点(0，0)且与曲线y=^x在点(1，2)处相切，则=________.

答案：1、2(ln2-1)
解析：
第16题：

设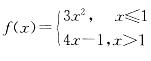，则f(x)在点x=1处：

A.不连续
B.连续但左、右导数不存在
C.连续但不可导
D.可导

答案：C
解析：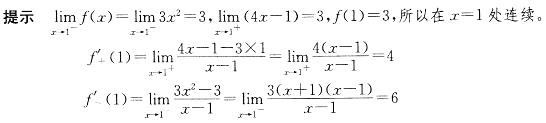

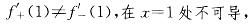所以f(x)在点x=1处连续不可导。
第17题：

若f(x)有连续导数，下列等式中一定成立的是（）

答案：A
解析：
第18题：

对于二元函数z=f（x，y），下列有关偏导数与全微分关系中正确的命题是（）。
- A、偏导数存在，则全微分存在
- B、偏导数连续，则全微分必存在
- C、全微分存在，则偏导数必连续
- D、全微分存在，而偏导数不一定存在
正确答案:B
第19题：

下列结论正确的是（）．
- A、z=f（x，y）在点（x，y）的偏导数存在是f（x，y）在该点连续的充分条件
- B、z=f（x，y）在点（x，y）连续是f（x，y）的偏导数存在的必要条件
- C、z=（x，y）在点（x，y）的偏导数存在是f（x，y）在该点可微分的充分条件
- D、z=（x，y）在点（x，y）连续是f（x，y）在该点可微分的必要条件
正确答案:D
第20题：

问答题
设z＝f（u），而u＝u（x，y）满足u＝y＋xφ（u）。若f和φ有连续导数，u存在偏导数，且xφ′（u）≠1，证明：∂z/∂x＝φ（u）∂z/∂y。

正确答案：
原方程u=y+xφ(u),两边分别对x、y求偏导得∂u/∂x=φ(u)+xφ′(u)∂u/∂x,∂u/∂y=1+xφ′(u)∂u/∂y。
即∂u/∂x=-φ(u)/[xφ′(u)-1],∂u/∂y=-1/[xφ′(u)-1]。
又∂z/∂x=(df/du)·(∂u/∂x)=(df/du)·[φ(u)/(1-xφ′(u))],∂z/∂y=(df/du)·(∂u/∂y)=(df/du)·[1/(1-xφ′(u))]。
则∂z/∂x=φ(u)∂z/∂y。
解析：暂无解析
第21题：

单选题
设f′（x0）＝f″（x0）＝0，f‴（x0）＞0，且f（x）在x0点的某邻域内有三阶连续导数，则下列选项正确的是（　　）。
A
f′（x₀）是f′（x）的极大值
B
f（x₀）是f（x）的极大值
C
f（x₀）是f（x）的极小值
D
（x₀，f（x₀））是曲线y＝f（x）的拐点

正确答案： D
解析：
已知f‴（x₀）＞0，则f″（x）在x₀点的某邻域内单调增加，又由f″（x₀）＝0，则在x₀点的某邻域内f_－″（x₀）与f_＋″（x₀）符号相反，故（x₀，f（x₀））是曲线y＝f（x）的拐点。
第22题：

单选题
设f（x）有连续的导数，则下列关系式中正确的是（　　）。[2013年真题]
A
∫f（x）dx＝f（x）
B
（∫f（x）dx）′＝f（x）
C
∫f′（x）dx＝f（x）dx
D
（∫f（x）dx）′＝f（x）＋C

正确答案： B
解析：
∫f（x）dx＝F（x）＋C，∫f′（x）dx＝f（x）＋C，（∫f（x）dx）′＝f（x）。
第23题：

单选题
设f（x）的二阶导数存在，且f′（x）=f（1-x），则下列式中何式可成立（）？
A
f″（x）+f′（x）=0
B
f″（x）-f′（x）=0
C
f″（x）+f（x）=0
D
f″（x）-f（x）=0

正确答案： C
解析：对已知式子两边求导。已知f′（x）=f（1-x），求导f″（x）=-f′（1-x），f（x）+f′（1-x）=0，将1-x代入式子f′（x）=f（1-x），得f′／（1-x）=f[1-（1-x）]=f（x），即f″（x）+f（x）=0

设f（x）有连续导数，则下列关系式中正确的是：

题目

相似考题

更多“设f（x）有连续导数，则下列关系式中正确的是： ”相关问题

相关内容