一平面简谐波的波动方程为y=0.02cos2π(10t-x/5) (SI)，则在t=0.25s时，处于平衡位置，且于坐标原点x=0最近的质元的位置是： A.±5m B.5m C.±1.25m D.1.25m

题目
一平面简谐波的波动方程为y=0.02cos2π(10t-x/5) (SI)，则在t=0.25s时，处于平衡位置，且于坐标原点x=0最近的质元的位置是：

A.±5m
B.5m
C.±1.25m
D.1.25m
相似考题

1.一横波的波动方程是t=0.25s，距离原点（x=0）处最近的波峰位置为（　　）。 A、 ±2、5mB、 ±7、5mC、 ±4、5mD、 ±5m

2.—平面简谐波沿x轴正方向传播，振幅A=0. 02m，周期T=0. 5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为： A.y=0.02cos2π(t/2-0.01x) (SI) B.y=0.02cos2π(2t-0.01x) (SI) C.y=0.02cos2π(t/2-100x) (SI) D.y=0.02cos2π(2t-100x) (SI)

3.一平面谐波沿x轴正方向传播，振幅A=0.02m，周期T=0.5s，波长λ=100m，原点处质元的初相位φ=0，则波动方程的表达式为( )。A. B.y=0.02cos2π(2t-0.01x)(SI) C. D.y=0.02cos2π(2t-100x)(SI)

4.一简谐波沿x轴正向传播，波的振幅为A，角频率为ω，波速为u。若以原点处的质元经平衡位置正方向运动时作为计时的起点，则该波的波动方程是( )。A.y=Acos[ω(t-x/u)+π/2] B.y=Acos[ω(t-x/u)-π/2] C.y=Acos[ω(t-x/u)+π] D.y=Acos[ω(t-x/u)-π/3]

更多“一平面简谐波的波动方程为y=0.02cos2π(10t-x/5) (SI)，则在t=0.25s时，处于平衡位置，且于坐标原点x=0最近的质元的位置是： ”相关问题

  • 第1题：

    一平面简谐波的波动方程为



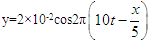
    （SI），对x=-2.5m处的质元，在t=0.25s时，它的（　　）。

    A、 动能最大，势能最大
    B、 动能最大，势能最小
    C、 动能最小，势能最大
    D、 动能最小，势能最小

    答案：D
    解析：
    在x=-2.5m处的质元的波动方程为：y=2×10-2cos2π(10t+0.5)。当t=0.25s时，y=2×10-2cos6π，此时质元处于最大位移处，故速度最小，即动能最小。在波动中，质元的动能和势能的变化是同相位的，同时达到最大值，又同时达到最小值，故势能此时也最小。

  • 第2题：

    一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI)，则在t=0. 1s时刻，x=2m处质元的振动位移是：
    A. 0. 01cm B. 0. 01m
    C. -0. 01m D. 0. 01mm


    答案：C
    解析：

  • 第3题：

    —平面简谐波的波动方程为y = 0. 02cos2π(10t-x/5)(SI)。t=0. 25s 时，处于平衡位置，且与坐标原点x=0最近的质元的位置是：

    A. ± 5 m
    B. 5m
    C. ±1. 25m
    D. 1. 25m

    答案：D
    解析：


    @##

  • 第4题：

    一平面简谐波的波动方程为，则在t=0.25s时刻，处于平衡位置，且与坐标原点x=0最近的质元的位置是（）。

    • A、x=±5m
    • B、x=5m
    • C、x=±1.25m
    • D、x=1.25m

    正确答案:C

  • 第5题：

    单选题
    一平面简谐波的波动方程为y＝2×10－2cos2π（10t－x/5）（SI），则在t＝0.25s时处于平衡位置，且与坐标原点x＝0最近的质元的位置是（　　）。[2012年真题]
    A

    x＝±5m

    B

    x＝5m

    C

    x＝±1.25m

    D

    x＝1.25m


    正确答案： C
    解析：
    在t＝0.25s时刻，处于平衡位置，y＝0，由简谐波的波动方程y＝2×10－2cos[2π（10×0.25－x/5）]＝0可知，cos[2π（10×0.25－x/5）]＝0，则2π（10×0.25－x/5）＝（2k＋1）π/2（k＝0，±1，±2，…）。由此可得：x＝5（9/4－k/2）。当x＝0时，k＝9/2。所以k取4或5；x＝±1.25时，与坐标原点x＝0最近。

  • 第6题：

    单选题
    一平面简谐波的波动方程为y＝0.01cos10π（25t－x）（SI），则在t＝0.1s时刻，x＝2m处质元的振动位移是（　　）。[2018、2011年真题]
    A

    0.01cm

    B

    0.01m

    C

    －0.01m

    D

    0.01mm


    正确答案： C
    解析：
    波动方程的意义有：①当x一定时，波动方程表示坐标为x的质点的振动方程。②当t一定时，波动方程表示t时刻各质点的位移。故在t＝0.1s时刻，x＝2m处质元的振动位移是：y＝0.01cos10π（25t－x）＝0.01cos10π（25×0.1－2）＝－0.01m。

  • 第7题：

    单选题
    一平面简谐波的波动方程为y＝2×10－2cos[2π（10t－x/5）]（SI），对x＝－2.5m处的质元，在t＝0.25s时，它的（　　）。[2016年真题]
    A

    动能最大，势能最大

    B

    动能最大，势能最小

    C

    动能最小，势能最大

    D

    动能最小，势能最小


    正确答案： A
    解析：
    在x＝－2.5m处的质元的波动方程为：y＝2×10－2cos2π（10t＋0.5）；当t＝0.25s时，y＝2×10－2cos6π，此时质元处于最大位移处，故速度最小，即动能最小。在波动中，质元的动能和势能的变化是同相位的，同时达到最大值，又同时达到最小值，故势能此时也最小。

  • 第8题：

    一平面简谐波的波动方程为y＝0.01cos10π（25t－x）（SI），则在t＝0.1s时刻，x＝2m处质元的振动位移是（　　）。

    A． 0.01cm
    B． 0.01m
    C． －0.01m
    D． 0.01mm

    答案：C
    解析：
    波动方程的意义有：①当x一定时，波动方程表示坐标为x的质点振动方程；②当t一定时，波动方程表示t时刻各质点的位移。故在t＝0.1s时刻，x＝2m处质元的振动位移是：y＝0.01cos10π（25t－x）＝0.01cos10π（25×0.1－2）＝－0.01m。

  • 第9题：

    一平面简谐波的波动方程为y=0.01cos10π(25t-x) (SI)，则在t=0. 1s时刻，x=2m处质元的振动位移是：

    A. 0. 01cm
    B. 0. 01m
    C. -0. 01m
    D. 0. 01mm

    答案：C
    解析：

  • 第10题：

    （2011）-平面简谐波的波动方程为y=0.01cos10π（25t-x）（SI），则在t=0.1s时刻，x=2m处质元的振动位移是：（）

    • A、0.01cm
    • B、0.01m
    • C、-0.01m
    • D、0.01mm

    正确答案:C

  • 第11题：

    一平面简谐波的波动方程为y=0.01cos10π（25t-x）（SI），则在t=0.1s时刻，x=2m处质元的振动位移是（）。

    • A、0.01cm
    • B、0.01m
    • C、-0.01m
    • D、0.01mm

    正确答案:C

  • 第12题：

    单选题
    一平面简谐波沿x轴正向传播，振幅A＝0.02m，周期T＝0.5s，波长λ＝100m，原点处质元初相位φ＝0，则波动方程的表达式（　　）。[2012年真题]
    A

    y＝0.02cos2π（t/2－0.01x）（SI）

    B

    y＝0.02cos2π（2t－0.01x）（SI）

    C

    y＝0.02cos2π（t/2－100x）（SI）

    D

    y＝0.002cos2π（2t－100x）（SI）


    正确答案： A
    解析：
    沿x轴正向传播的波动方程表达式为：y＝Acos[ω（t－x/u）＋φ0]。又u＝λ/T，ω＝2π/T，故波动方程写为：y＝Acos[2π（t/T－x/λ）＋φ0]。由于A＝0.02m，T＝0.5s，λ＝100m，φ0＝0，代入波动方程公式可得：y＝0.02cos2π（2t－0.01x）（SI）。

  • 第13题：

    单选题
    一平面简谐波的波动方程为y=0.01cos10π（25t-x）（SI），则在t=0.1s时刻，x=2m处质元的振动位移是（　　）。[2011年真题]
    A

    0.01cm

    B

    0.01m

    C

    -0.01m

    D

    0.01mm


    正确答案： A
    解析：
    波动方程的意义有：①当x一定时，波动方程表示坐标为x的质点的振动方程；②当t一定时，波动方程表示t时刻各质点的位移。故在t=0.1s时刻，x=2m处质元的振动位移是：y=0.01cos10π（25t-x）=0.01cos10π（25×0.1-2）=-0.01m。

  • 第14题：

    单选题
    一平面简谐波的波动方程为，则在t=0.25s时刻，处于平衡位置，且与坐标原点x=0最近的质元的位置是（）。
    A

    x=±5m

    B

    x=5m

    C

    x=±1.25m

    D

    x=1.25m


    正确答案： A
    解析： 暂无解析

相关内容