直线L：(x-2)/1=(y-3)/2=(z-1)/1与平面Ⅱ：2x+y-4z=6的位置关系是( ).A.L垂直于Ⅱ B.L与Ⅱ相交，但不垂直 C.L与Ⅱ平行，且L不在Ⅱ上 D.L在Ⅱ上

题目
直线L：(x-2)/1=(y-3)/2=(z-1)/1与平面Ⅱ：2x+y-4z=6的位置关系是( ).

A.L垂直于Ⅱ
B.L与Ⅱ相交，但不垂直
C.L与Ⅱ平行，且L不在Ⅱ上
D.L在Ⅱ上
相似考题

1.已知曲线C为y= 2x2，直线l为y= 4x．（10分）(1)求由曲线C与直线l所围成的平面图形的面积S；(2)求过曲线C且平行于直线l的切线方程．

2.设有直线L1：(x-1)/(-2)=(y+1)/2=z+2和L2：x=(y-2)/(-4)=z-1，则L1和L2的夹角φ是( )A.π/6 B.π/4 C.π/3 D.π/2

3.设平面方程x+y+Z+1=0，直线的方程是l-x=y+1= z，则直线与平面： (A)平行 （B)垂直 (C)重合 (L)相交但不垂直

4.直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是( ).A.直线L与平面∏平行 B.直线L与平面∏垂直 C.直线L在平面∏上 D.直线L与平面∏相交，但不垂直

更多“直线L：(x-2)/1=(y-3)/2=(z-1)/1与平面Ⅱ：2x+y-4z=6的位置关系是( ).”相关问题

  • 第1题：

    设平面方程:x + y + z-1 = 0，直线的方程是1-x = y + 1=z，则直线与平面：
    A.平行 B.垂直 C.重合 D.相交但不垂直


    答案：D
    解析：

  • 第2题：

    已知直线l⊥平面α，直线m属于平面β，下面四个命题：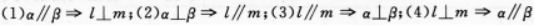

    其中正确的两个命题是()

    A.(1)与(2)
    B.(3)与(4)
    C.(2)与(4)
    D.(1)与(3)

    答案：D
    解析：
    【考情点拔】本题主要考查的知识点为直线与平面的位置关系． 【应试指导】(1)正确，l⊥α，α∥β，则l⊥β，又m属于β，∴l⊥m
    (2)错，∵l与m可能有两种情况：平行或异面．
    (3)正确，∵l⊥α，l∥m，则m⊥α，又m属于β，∴α⊥β．
    (4)错，∵a与β有两种情况：平行、相交．

  • 第3题：

    直线 与平面π：x+y+z=2的位置关系

    A、平行
    B、相交但不垂直
    C、垂直
    D、直线f在平面上

    答案：B
    解析：
    由题意得：直线L的方向向量为m=(2，一l，一3)，平面霄的法向量即=(1，1，1)，易知m与，l不共线，且m·n#0，而直线l上的点(1，一l，2)在平面π上，故两者相交但不垂直。故选择B。

  • 第4题：

    直线l：（x+3）／2=（y+4）／1=z／3与平面π：4x-2y-2z=3的位置关系为：（）

    • A、相互平行
    • B、L在π上
    • C、垂直相交
    • D、相交但不垂直

    正确答案:A

  • 第5题：

    （x^3-6x^2+11x-6，x^2-3x+2）=（）。

    • A、（x-1）（x+2）
    • B、（x+1）（x-2）
    • C、（x-1）（x-2）
    • D、（x-2）（x-3）

    正确答案:C

  • 第6题：

    直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）.

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第7题：

    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.

    • A、（x-4）/2=（y+1）/0=（z-3）/5
    • B、（x-4）/2=（y+1）/1=（z-3）/5
    • C、（x+4）/2=（y-1）/0=（z+3）/5
    • D、（x+4）/2=（y-1）/1=（z+3）/5

    正确答案:B

  • 第8题：

    单选题
    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．
    A

    直线L与平面∏平行

    B

    直线L与平面∏垂直

    C

    直线L在平面∏上

    D

    直线L与平面∏相交，但不垂直


    正确答案： C
    解析： 暂无解析

  • 第9题：

    单选题
    直线L：（x＋3）/（－2）＝（y＋4）/（－7）＝z/3与平面∏：4x－2y－2z＝3的关系是（　　）。
    A

    平行

    B

    直线L在平面∏上

    C

    垂直相交

    D

    相交但不垂直


    正确答案： D
    解析：
    平面∏：4x－2y－2z＝3的法向量为n(→)＝{2，－1，－1}，直线L：（x＋3）/（－2）＝（y＋4）/（－7）＝z/3的方向向量l(→)＝{－2，－7，3}，由于l(→)·n(→)＝（－2）×2＋（－7）×（－1）＋3×（－1）＝0，所以直线与平面平行。

  • 第10题：

    单选题
    直线l：（x+3）／2=（y+4）／1=z／3与平面π：4x-2y-2z=3的位置关系为：（）
    A

    相互平行

    B

    L在π上

    C

    垂直相交

    D

    相交但不垂直


    正确答案： B
    解析： s={2，1，3}，n={4，-2，-2}，s·n=0，表示直线和平面平行或直线在平面上，再进一步说明直线L和平面π相互平行。取直线上任一点不满足平面方程，从而得到结论A。

  • 第11题：

    单选题
    直线5x－2y＋1＝0与直线15x－6y＋m＝0的位置关系是（　　）．
    A

    平行

    B

    垂直

    C

    平行或重合

    D

    相交而不垂直


    正确答案： C
    解析：
    由题意可知两直线的斜率相等，当m＝3时，两直线重合，当m≠3时，两直线平行，所以两直线平行或重合．

  • 第12题：

    单选题
    过点（4，-1，3）且平行于直线L：（x-3）/2=y=（z-1）/5的直线方程为（）.
    A

    （x-4）/2=（y+1）/0=（z-3）/5

    B

    （x-4）/2=（y+1）/1=（z-3）/5

    C

    （x+4）/2=（y-1）/0=（z+3）/5

    D

    （x+4）/2=（y-1）/1=（z+3）/5


    正确答案： A
    解析： 暂无解析

  • 第13题：

    圆心在Y轴上，且与直线χ+y-3=0及χ-y-1=0都相切的圆的方程为_____．


    答案：
    解析：
    【答案】
    【考情点拨】本题主要考查的知识点为圆的切线的性质．
    【指导指导】设圆的方程为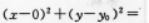r2(如图)

  • 第14题：

    直线绕原点按逆时针方向旋转30°后所得直线与圆(x-2)2+y2=3的位置关系是（ ）。

    A.直线过圆心
    B.直线与圆相交，但不过圆心
    C.直线与圆相切
    D.直线与圆相离

    答案：C
    解析：

  • 第15题：

    在空间直角坐标系下。试判定直线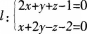与平面π：3x—y+2z+1=0的位置关系，并求出直线Z与平面π的夹角的正弦值。


    答案：
    解析：
    平面π的法向量为n=(3，一l，2)；
    平面2x+γ+z=0的法向量为nl=(2，1，1)，平面x+2y一2=0的法向量为n2=(1，2，一l)，则直线l的方向向量为mn=一9—3+6—6，可知直线f与平面π相交。设直线Z与平面π的夹角为θ，则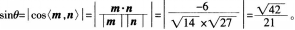

  • 第16题：

    已知两直线l1：x／2=（y+2）／-2=（1-x）／-1和l2：（x-1）／4=（y-3）／M=（z+1）／-2相互垂直，则M的值为：（）

    • A、3
    • B、5
    • C、-2
    • D、-4

    正确答案:B

  • 第17题：

    在标高投影图上怎样判断空间两平面的位置关系，空间直线与平面的位置关系？


    正确答案: 在平面标高投影图中，若两个平面的等高线相互平行，倾向相同，平距相等，则空间两平面彼此平行。在平面标高投影图上，若两平面等高线平行，倾向相反，则空间两平面相交。在平面标高投影图上，若两平面的等高线平行，倾向相同，但倾角不等则空间两平面相交。在平面标高投影图上，若两平面同名等高线相交，则空间两平平相交。
    直线位于平面内，直线与平面平行，直线与平面相交。

  • 第18题：

    直线L1：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）．

    • A、直线L与平面∏平行
    • B、直线L与平面∏垂直
    • C、直线L在平面∏上
    • D、直线L与平面∏相交，但不垂直

    正确答案:A

  • 第19题：

    单选题
    直线L：2x=5y=z-1与平面∏：4x-2z=5的位置关系是（）.
    A

    直线L与平面∏平行

    B

    直线L与平面∏垂直

    C

    直线L在平面∏上

    D

    直线L与平面∏相交，但不垂直


    正确答案： A
    解析： 暂无解析

  • 第20题：

    单选题
    已知两直线l1：x／2=（y+2）／-2=（1-x）／-1和l2：（x-1）／4=（y-3）／M=（z+1）／-2相互垂直，则M的值为：（）
    A

    3

    B

    5

    C

    -2

    D

    -4


    正确答案： A
    解析： 暂无解析

  • 第21题：

    单选题
    曲面z=y+lnx／z在点（1，1，1）处的法线方程是：（）
    A

    （x-1）／1=（y-1）／1=（z-1）／-1

    B

    （x-1）／1=（y-1）／1=（z-1）／-2

    C

    （x-1）／1=（y-1）／-1=（z-1）／-2

    D

    x+y-z=1


    正确答案： B
    解析： 暂无解析

  • 第22题：

    单选题
    （x^3-6x^2+11x-6，x^2-3x+2）=（）。
    A

    （x-1）（x+2）

    B

    （x+1）（x-2）

    C

    （x-1）（x-2）

    D

    （x-2）（x-3）


    正确答案： C
    解析： 暂无解析

  • 第23题：

    问答题
    求过点M（－1，0，1）且垂直于直线（x－2）/3＝（y＋1）/（－4）＝z/1又与直线（x＋1）/1＝（y－3）/1＝z/2相交的直线方程。

    正确答案：
    过点M(-1,0,1)且垂直于直线(x-2)/3=(y+1)/(-4)=z/1的平面方程为3x-4y+z+2=0。该平面与直线(x+1)/1=(y-3)/1=z/2的交点为(12,16,26),则该交点与点M(-1,0,1)形成的直线方程为(x+1)/13=y/16=(z-1)/25,即为所求。
    解析： 暂无解析

相关内容