一平面简谐波在t=0时刻的波形如图3所示，波速u=0.08m·s-1，则波动表达式为( )。

题目
一平面简谐波在t=0时刻的波形如图3所示，波速u=0.08m·s-1，则波动表达式为( )。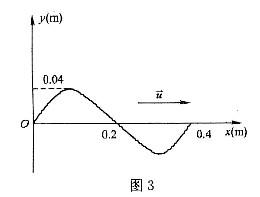

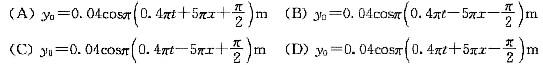
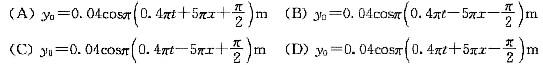
相似考题

1.一平面简谐波在t=0时的波形曲线如图所示，设波沿x轴正向传播，波速υ=1.6×10-1m/s，则该波的角频率ω=______rad/s，坐标原点处的质元作简谐振动的表达式为y=_____(SI)。

2.已知一列平面简谐波沿Ox轴正向传播，波速u=400m·s-1，频率υ=20Hz，t=0时刻的波形曲线如图3所示，则波动表达式为( )。

3.一平面简谐波沿X轴正向传播，已知x=L(L0)，波速为u，那么x=0处质点的振动方程为： A. y=Acos[w(t+l/u)+Φ0] B.y=Acos[w(t-l/u)+Φ0] C. y=Acos[wt+l/u+Φ0] D. y=Acos[wt-l/u+Φ0]

4.一平面简谐波沿x轴正向传播，已知P点(xp＝L)的振动方程为y＝Acos(ωt＋φ0)，则波动方程为( )。A. B. C.y＝Acos[t－(x/u)] D.

更多“一平面简谐波在t=0时刻的波形如图3所示，波速u=0.08m·s-1，则波动表达式为( )。”相关问题

  • 第1题：

    一平面简谐波表达式为y=-0.05sinπ(t-2x)(SI)，则该波的频率v(Hz)、波速u(m/s)及波线上各点振动的振幅A(m)依次为：


    答案：C
    解析：

  • 第2题：

    一平面简谐波在



    时刻的波形图如图示·该波以u=36m/s的速度沿x轴正向传播，则在t=0时刻O点的初位相是( )。


    A.π/4
    B.π/2
    C.π/3
    D.π

    答案：B
    解析：
    由平面简谐波标准波动方程，依题意代入各已知条件可得

  • 第3题：

    —平面谐波的表达式为y = 0. 03cos(8t+3x + π/4)(SI)，则该波的频率v (Hz),波长λ(m)和波速u(m/s)依次为：


    答案：A
    解析：

  • 第4题：

    一简谐波向右传播，某时刻的波形如图6-3所示．已知波的周期为T，则A点的振动传到B点所用的时间为（　　）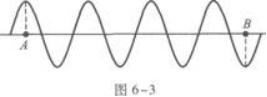

    A.3T
    B.3．5T
    C.4T
    D.4．5T

    答案：B
    解析：
    本题考查的知识点是波形图． 波动是振动在介质中的传播过程，波从A点传播到B点时就把A点的振动状态传播到了B点．
    由图6-3见，从A到B之间包括了3．5个完整波，一个完整波的距离是波长λ，因此AB之间的距离
    s＝3．5λ
    由此可得波从A传播到B所用的时间为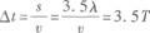

    选B．
    本题是一道很简单的选择题，但有些考生错选C．图6-3中给出的整个波形为4个完整波，粗心的考生就选C．这完全是审题不慎引起的，应注意避免．题中明确求由A到B的时间．

  • 第5题：

    横波以波速u沿x轴正向传播，t时刻波形曲线如图2-9所示，则该时刻（ ）。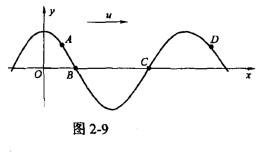

    A. A点速度小于零 B. B点静止不动 C. C点向上运动 D. D点速度大于零


    答案：D
    解析：
    提示：t+Δt时刻，波形曲线向右移动。由此断定ABCD各点的运动方向。

  • 第6题：

    一平面简谐波的波动方程为（SI制），则它的振幅为（）、角频率为（）、周期为（）、波速为（）、波长为（）。


    正确答案:0.01m；20πrad/s；0.1s；40m/s；4m

  • 第7题：

    一平面简谐波沿x轴正向传播，已知x=L（L<λ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）

    • A、y=Acosω［t-（x-L）／u]
    • B、y=Acosω［t-（x+L）／u]
    • C、y=Acosω［t+（x+L）／u]
    • D、y=Acosω［t+（x-L）／u]

    正确答案:A

  • 第8题：

    单选题
    一平面简谐波沿X轴正向传播，已知x=L（Lt，波速为u，那么x=0处质点的振动方程为（）。
    A

    y=Acosω（t+L/u）

    B

    y=Acosω（t-L/u）

    C

    y=Acos（ωt+L/u）

    D

    y=Acos（ωt-L/u）


    正确答案： D
    解析： 暂无解析

  • 第9题：

    单选题
    一平面简谐波沿X轴正向传播，已知x=1（10），波速为u，那么x=0处质点的振动方程为：（）
    A

    y=Acos［w（t+1/u）+φ0］

    B

    y=ACOS［w（t-1/u）+φ0］

    C

    y=Acos［wt+1/u+φ0］

    D

    y=Acos［wt-1/u+φ0］


    正确答案： D
    解析： 以x=L处为原点，写出波动方程，再令x=-L

  • 第10题：

    单选题
    平面简谐波沿x轴正方向传播，其振幅为A，频率为v，设t=t 0时刻的波形如图所示，则x=0处质点的振动方程是（）。
    A

    y=Acos［2πv（t+t 0）+π／2］

    B

    y=Acos［2πv（t-t 0）+π／2］

    C

    y=Acos［2πv（t-t 0）-π／2］

    D

    y=Acos［2πv（t-t 0）+π］


    正确答案： B
    解析： 暂无解析

  • 第11题：

    一平面简谐波的波动方程为y=0.1cos(3πt-πx+π)(SI) ，t=0时的波形曲线如图所示，则下列叙述中哪个正确？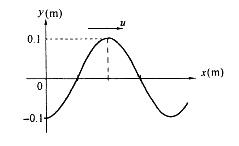


    A.O点的振幅为0.1m
    B.频率r=3Hz
    C.波长为2m
    D.波速为9m/s

    答案：C
    解析：
    提示：u=λv，w=2πv。

  • 第12题：

    一平面简谐波波动表达式为，式中x，t分别以cm，s为单位，则x=4cm位置处的质元在t=1s时刻的振动速度v为( )。

    A、v=0
    B、v=5cm·s-1
    C、v=-5πcm·s-1
    D、v=-10πcm·s-1

    答案：A
    解析：
    已知波动表达式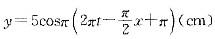，则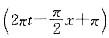，当时x=4cm，t=1s时，v=-50sinπ=0

  • 第13题：

    一平面简谐波的波动方程为y=0.1cos(3πt-πx+π)(SI) ，t=0时的波形曲线如图所示，则下列叙述中哪个正确？

    A.O点的振幅为0.1m B.频率r=3Hz
    C.波长为2m D.波速为9m/s


    答案：C
    解析：
    提示：u=λv，w=2πv。

  • 第14题：

    一列横波在t=0时刻的波形如图中实线所示，在t=1s时刻的波形如图中虚线所示，由此可以判定此波的（??）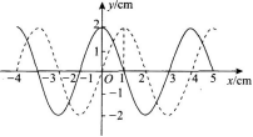

    A.波长一定是5cm
    B.周期可能是4s
    C.振幅一定是4cm
    D.传播速度一定是1cm／s

    答案：B
    解析：

  • 第15题：

    如图2-8所示，一平面简谐波沿x轴正向传播，t=0时的波形图如图所示，波速u= 20m/s,则P处介质点的振动方程是（）。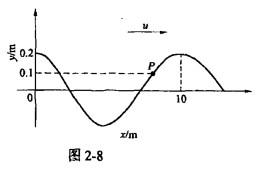

    A. y = 0.2cos(4πt + π/3)(SI) B. y = 0.2cos(4πt －π/3)(SI)
    C.y= 0.2cos(4πt + 2π/3)(SI) D. y= 0.2cos(4πt －2π/3)(SI)


    答案：A
    解析：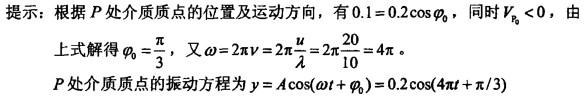

  • 第16题：

    一平面简谐波沿X轴正向传播，已知x=L（L<λ）处质点的振动方程为y=Acos（∞t+φ0），波速为u，那么x=0处质点的振动方程为：（）

    • A、y=Acos[ω（t+L／u）+φ0]
    • B、y=Acos[ω（t-L／u）+φ0]
    • C、y=Acos[ωt+L／u+φ0]
    • D、y=Acos[ωt-L／u+φ0]

    正确答案:A

  • 第17题：

    一平面简谐波沿x轴负方向传播，其振幅A=0.01m，频率v=550Hz，波速u=330m·s-1。若t=0时，坐标原点O处质元达到负的最大位移，则该波的表达式为（）。

    • A、y=0.01cos[2π（550t+1.67x）+π]
    • B、y=0.01cos[2π（550t-1.67x）+π]
    • C、y=0.01cos[2π（550t+1.67x）-π]
    • D、y=0.01cos[2π（550t-1.67x）-π]

    正确答案:A

  • 第18题：

    单选题
    一平面简谐波沿X轴正向传播，已知x=L（L0），波速为u，那么x=0处质点的振动方程为：（）
    A

    y=Acos[ω（t+L／u）+φ0]

    B

    y=Acos[ω（t-L／u）+φ0]

    C

    y=Acos[ωt+L／u+φ0]

    D

    y=Acos[ωt-L／u+φ0]


    正确答案： C
    解析： 以x=L处为原点，写出波动方程，再令x=-L。

  • 第19题：

    单选题
    一平面简谐波沿x轴正向传播，已知x=L（L<λ）处质点的振动方程为y=Acosωt，波速为u，则波动方程为（）
    A

    y=Acosω［t-（x-L）／u]

    B

    y=Acosω［t-（x+L）／u]

    C

    y=Acosω［t+（x+L）／u]

    D

    y=Acosω［t+（x-L）／u]


    正确答案： A
    解析： 暂无解析

相关内容