为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:请根据上述结果,从下列备选答案中选出正确答案。 根据样本观测值和估计值计算回归系数β2的t统计量,其值为f=8.925,根据显著性水平(α=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。A.接受原假设,拒绝备择假设B.拒绝原假设,接受备择假设C.在95%的置信水平下,图.png是由β2
题目
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
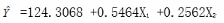
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为f=8.925,根据显著性水平(α=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。
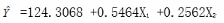
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为f=8.925,根据显著性水平(α=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。
A.接受原假设,拒绝备择假设
B.拒绝原假设,接受备择假设
C.在95%的置信水平下,图.png是由β2 =0这样的总体产生的
D.在95%的置信水平下,居住面积对居民家庭电力消耗量的影响是显著的
B.拒绝原假设,接受备择假设
C.在95%的置信水平下,图.png是由β2 =0这样的总体产生的
D.在95%的置信水平下,居住面积对居民家庭电力消耗量的影响是显著的
相似考题
更多“为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: ”相关问题
-
第1题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。 答案:B,D解析:根据样本观测值和估计值计算回归系数的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。
答案:B,D解析:根据样本观测值和估计值计算回归系数的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。 -
第2题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。A.在Y的总变差中,有92.35%可以由解释变量X1和X2解释
B.在Y的总变差中,有92.35%可以由解释变量置解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量X1和X2决定的答案:A解析:多重判定系数是多元线性回归平方和占总平方和的比例,计算公式为:R2
它可以理解为:在因变量y的总变差中被估计的多元线性回归方程所解释的比例。 -
第3题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。A.H0:β1=β2=0;H1:β1≠β2≠0
B.H0:β1=β2≠0;H1:β1≠β2=0
C.H0:β1≠β2≠0;H1:β1=β2≠0
D.H0:β1=β2=0;H1:β1至少有一个不为零答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0:原假设认为所有系数均为0;备择假设认为所有系数不全为0。 -
第4题:
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果

描述城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入之间关系适合的图形是( )。A.直方图
B.折线图
C.散点图
D.雷达图答案:C解析: -
第5题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: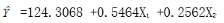
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。
A.H0: β1 =β2 =0;H1: β1≠β2 ≠0
B.H0: β1 =β2 ≠0;H1: β1≠β2 =0
C.H0: β1 ≠β2 ≠0;H1: β1=β2 ≠0
D.H0: β1 =β2 =0;H1: β1至少有一个不为零答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0:原假设认为所有系数均为0;备择假设认为所有系数不全为0。 -
第6题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
请根据上述结果,从下列备选答案中选出正确答案。
回归系数β2=0.2562的经济意义为()。
A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均减少0.2562千瓦小时答案:B解析: -
第7题:
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果

如果 ,根据表3,下列说法正确的是( )。A.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系 显著
B.城镇居民家庭人均可支配收入对城镇居民家庭人均食品消费支出的线性关系不显著
C.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系显著
D.食品类居民消费价格指数对城镇居民家庭人均食品消费支出的线性关系不显著答案:A,C解析: -
第8题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: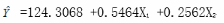
请根据上述结果,从下列备选答案中选出正确答案。
根据计算上述回归方程式的多重判定系数为0.9235,其正确的含义是()。
A.在Y的总变差中,有92.35%可以由解释变量Xl和X2解释
B.在Y的总变差中,有92.35%可以由解释变量Xl解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量Xl和X2决定的答案:A解析:多重判定系数是多元线性回归平方和占总平方和的比例,计算公式为: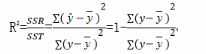
判定系数R2度量了多元线性回归方程的拟合程度,它可以解释为:在因变量Y的总变差中被估计的多元线性回归方程所揭示的比例。 -
第9题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:

根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有( )。 答案:B,D解析:根据样本观测值和估计值计算回归系数β2的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。
答案:B,D解析:根据样本观测值和估计值计算回归系数β2的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。 -
第10题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
根据上述回归方程式计算的多重判定系数为0.9235,其正确的含义是( )。A.在Y的总变差中,有92.35%可以由解释变量X1和X2解释
B.在Y的总变差中,有92.35%可以由解释变量X1解释
C.在Y的总变差中,有92.35%可以由解释变量X2解释
D.在Y的变化中,有92.35%是由解释变量X1和X2决定的答案:A解析:决定系数是多元线性回归平方和占总平方和的比例,计算公式为: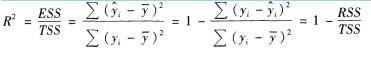
决定系数R2度量了多元线性回归方程的拟合程度,它可以解释为:在因变量Y的总变差中被估计的多元线性回归方程所揭示的比例。 -
第11题:
为预测我国居民对电子表的需求量,定义变量“商品价格”(x1,单位:元/件)、“消费者人均月收入”(x2,单位:元)及“商品需求量”(y,单位:件),建立多元线性回归方程如下:y=4990.519-35.66597x1+6.19273x2,请根据上述结果,从备选答案中选出正确答案。根据计算上述回归方程式的多重判定系数为0.9540,其正确的含义是()。
- A、在Y的变化中,有95.40%是由解释变量x1和x2决定的
- B、在Y的总变差中,有95.40%可以由解释变量x2解释
- C、在Y的总变差中,有95.40%可以由解释变量x1解释
- D、在Y的总变差中,有95.40%可以由解释变量x1和x2解释
正确答案:D -
第12题:
多选题回归系数β2=0.2562的经济意义为( )。A我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B在其他条件不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C在其他条件不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562千瓦小时
正确答案: A,D解析:
回归系数β表示在其他条件保持不变的情况下,该自变量每变动一个单位,因变量平均变动β个单位。 -
第13题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
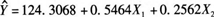
请根据上述结果,从下列备选答案中选出正确答案。
根据样本观测值和估计值计算回归系数β2的t统计量,其值为t=8.925,根据显著性水平(a=0.05)与自由度,由t分布表查得t分布的右侧临界值为2.431,因此,可以得出的结论有()。
 答案:B,D解析:根据样本观测值和估计值计算回归系数β2的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。
答案:B,D解析:根据样本观测值和估计值计算回归系数β2的t统计量为8.925,大于右侧临界值2.431,因而检验显著,拒绝原假设,接受备择假设。β2显著不等于0,即在95%的置信水平下,X2对Y的影响是显著的。 -
第14题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示:
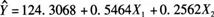
请根据上述结果,从下列备选答案中选出正确答案。
检验回归方程是否显著,正确的假设是()。
 答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0:原假设认为所有系数均为0;备择假设认为所有系数不全为0。
答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0:原假设认为所有系数均为0;备择假设认为所有系数不全为0。 -
第15题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下
请根据上述结果,从下列备选答案中选出正确答案。
对于多元线性回归模型,以下假设中正确的有()。A.因变量与自变量之间的关系为线性关系
B.随机误差项的均值为1
C.随机误差项之间是不独立的
D.随机误差项的方差是常数答案:A,D解析:多元线性回归模型的假定为:①因变量与自变量之间的关系为线性关系:②随机误差项的均值为0;③随机误差项之间是不相关的;④随机误差项的方差是常数;⑤自变量与随机误差项不相关。 -
第16题:
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果

根据表1~表3的输出结果可以得出( )。A.回归方程为:
B.城镇居民家庭人均食品消费支出与城镇居民家庭人均可支配收入和食品类居民消费价格指数的总体相关程度为87.7%
C.多元回归分析中拟合优度大小应根据判定系数( )来衡量
D.多元回归分析中拟合优度大小应根据调整后的判定系数( )来衡量答案:A,B,D解析: -
第17题:
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果

城镇居民家庭人均食品消费支出、城镇居民家庭人均可支配收入和食品类居民消费价格指数数据属于( )。A.一手数据
B.二手数据
C.实验数据
D.定性数据答案:B解析: -
第18题:
(一)将我国31个省(自治区、直辖市)某年度城镇居民家庭人均食品消费支出(y,单位:元)、城镇居民家庭人均可支配收入(x1,单位:元)和食品类居民消费价格指数(x2,单位:上年=100)进行回归分析,得到如表1~表3所示的输出结果:
表 1 回归方程的输出结果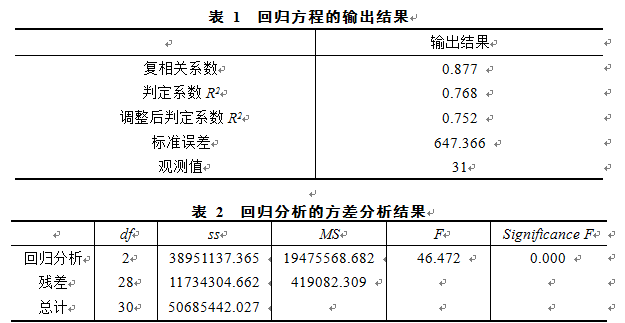
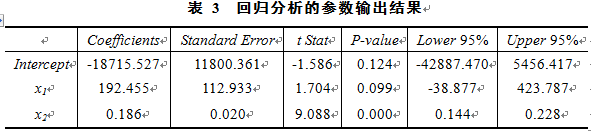
如果 ,根据表2,下列说法正确的是( )。A.F检验的假设为:
B.F检验的假设为:
C.回归方程的线性关系显著
D.回归方程的线性关系不显著答案:B,C解析: -
第19题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(单位:千瓦小时)与可支配收入(Xl,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: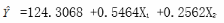
请根据上述结果,从下列备选答案中选出正确答案。
对于多元线性回归模型,以下假设中正确的有()。
A.因变量与自变量之间的关系为线性关系
B.随机误差项的均值为1
C.随机误差项之间是不独立的
D.随机误差项的方差是常数答案:A,D解析:多元线性回归模型的假定为:①因变量与自变量之间的关系为线性关系;⑦随机误差项的均值为0;③随机误差项之间是不相关的;④随机误差项的方差是常数;⑤自变量与随机误差项不相关。 -
第20题:
根据下面资料,回答79-82题
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: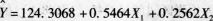
据此回答以下题目。
回归系数β2的经济意义为( )A.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0.2562.千瓦小时答案:B解析:回归系数β表示在其他自变量保持不变的情况下,该自变量每变动一个单位,因变量变动口个单位。 -
第21题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: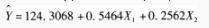
检验回归方程是否显著,正确的假设是()。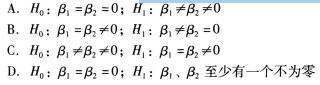 答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0,也即原假设认为所有系数均为0;备择假设认为所有系数不全为0。
答案:D解析:检验回归方程是否显著就是要检验回归方程中的所有系数是否同时为0,也即原假设认为所有系数均为0;备择假设认为所有系数不全为0。 -
第22题:
为预测我国居民家庭对电力的需求量,建立了我国居民家庭电力消耗量(Y,单位:千瓦小时)与可支配收入(X1,单位:百元)、居住面积(X2,单位:平方米)的多元线性回归方程,如下所示: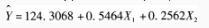
回归系数β2的经济意义为()。A.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
B.在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
C.在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0.2562千瓦小时
D.我国居民家庭居住面积每增加l平方米,居民家庭电力消耗量平均减少0.2562千瓦小时答案:B解析:回归系数β表示在其他自变量保持不变的情况下,该自变量每变动一个单位,因变量变动口个单位。 -
第23题:
不定项题A我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时
B在可支配收入不变的情况下,我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时
C在可支配收入不变的情况下,我国居民家庭居住面积每减少1平方米,居民家庭电力消耗量平均增加0. 256 2千瓦小时
D我国居民家庭居住面积每增加1平方米,居民家庭电力消耗量平均减少0. 256 2千瓦小时
正确答案: D解析:
