某消费者购买xy两种商品其预算线方程是50=x＋y,可知他的总收入为50。()此题为判断题(对，错)。

题目
某消费者购买xy两种商品其预算线方程是50=x＋y,可知他的总收入为50。()

此题为判断题(对，错)。

相似考题

1.市场商品需求量,是指计划内消费者在市场上购买商品的货币总额。()此题为判断题(对，错)。

2.价格变化是指在收入不变条件下如果两种商品的价格同比例下降,那么预算线将保持斜率不变并向外平移。如果两种商品的价格同比例上升,那么预算线将保持斜率不变并向内平移。()此题为判断题(对，错)。

3.收入变化是指在两种商品的价格不变的条件下收入增加将导致预算线向外平移,收入减少将导致预算线向内平移。()此题为判断题(对，错)。

4.消费者的购买活动,在完成商品购买后就结束了。( )此题为判断题(对，错)。

更多“某消费者购买xy两种商品其预算线方程是50=x＋y,可知他的总收入为50。() 此题为判断题(对，错)。”相关问题

  • 第1题：

    消费者购买商品或接受服务,其只有在财产受到损害时,才享有依法获得赔偿的权利。()

    此题为判断题(对，错)。


    答案：错误

  • 第2题：

    预算约束线以外的点,消费者则可能达到。()

    此题为判断题(对，错)。


    正确答案:×

  • 第3题：

    如果某商品价格与其销售总收入呈反方向变动关系,则可知,其需求富有弹性。()

    此题为判断题(对，错)。


    正确答案：对

  • 第4题：

    消费者在购买、使用商品的时候,发现商品有缺陷,如有毒食品,可以直接没收该商品。()

    此题为判断题(对，错)。


    正确的答案是“错”。

  • 第5题：

    消费者权益是指消费者为满足生活需要而购买、使用商品或服务时所享有的权力和利益。()

    此题为判断题(对，错)。


    参考答案：√

  • 第6题：

    消费动机是消费者购买房地产商品的内在原因。()

    此题为判断题(对，错)。


    参考答案：正确

  • 第7题：

    消费者均衡点是无差异曲线和预算线的切点。()

    此题为判断题(对，错)。


    参考答案：√

  • 第8题：

    冲动型购买行为即消费者以商品价格作为购买商品的标准。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第9题：

    消费者只享有知悉其购买、使用的商品的真实情况的权利。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第10题：

    知情权是指消费者享有知悉其购买、使用的商品或者接受服务真实情况的权利。

    此题为判断题(对，错)。


    正确答案：√

  • 第11题：

    某消费者消费X和Y两种商品所获得的效用函数为：U=XY+Y，预算约束为：PX X + PYY = I，求： 说明X和Y之间是替代品、互补品还是独立商品


    答案：
    解析：
    X与Y两种商品之间的需求交叉价格弹性为：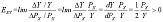

    也就是说随着商品X的价格上升，消费者将会增加对商品Y的购买。因此两种商品是替代品的关系。

  • 第12题：

    判断题
    预算线表示消费者在既定收入下能够购买到的两种商品不同数量组合点的轨迹。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第13题：

    消费者在购买使用商品时，其合法权受到损害，可以向生产者要求赔偿。

    此题为判断题(对，错)。


    正确答案：×

  • 第14题：

    如果某商品价格与其销售总收入正相关,则可知,其需求富有弹性。()

    此题为判断题(对，错)。


    正确答案：错

  • 第15题：

    选购品指消费者对其有特殊偏好并愿意花较多时间去购买的商品。()

    此题为判断题(对，错)。


    正确答案：错

  • 第16题：

    通过雷诺转换可知时均速度满足连续方程。()

    此题为判断题(对，错)。


    参考答案：错误

  • 第17题：

    消费者为个人和家庭生活需要而购买商品和劳务的行为，称为购买行为。

    此题为判断题(对，错)。


    正确答案：√

  • 第18题：

    商品降价幅度以30%~50%为宜。该说法()。

    此题为判断题(对，错)。


    参考答案：错

  • 第19题：

    所谓购买行为,是指消费者为满 足某种需要而发生的购买商品的 一切活动。()

    此题为判断题(对，错)。


    正确答案是：正确

  • 第20题：

    消费者其实并不真的是为商品的成本付费,他是为商品的价值感而付费。()

    此题为判断题(对，错)。


    正确答案：正确

  • 第21题：

    如果两种商品价格相同,对消费者来说,这两种商品的效用一般是相同的。()

    此题为判断题(对，错)。


    参考答案：×

  • 第22题：

    预算线斜率是两种商品价格的负比率。

    此题为判断题(对，错)。


    正确答案：√

  • 第23题：

    某消费者消费X和Y两种商品所获得的效用函数为：U=XY+Y，预算约束为：PX X + PYY = I，求： X、Y的需求函数


    答案：
    解析：
    求解消费者效用最大化时要满足：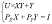

    通过构造拉格朗日辅助函数得：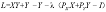

    求得其一阶导数为并令其为0：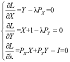

    得： X的需求函数为：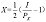

    Y的需求函数为：

相关内容