已知Lxx=∑(x－mean(x))2=400,Lyy=∑(y－mean(y))2=3000,Lxy=∑(x－mean(x))·(y－mean(y))=－1000;则相关系数r=()。注:mean(x)、mean(y)分别为x,y的均值。A.0.925B.-0.913C.0.957D.0.913

题目

已知Lxx=∑(x－mean(x))2=400,Lyy=∑(y－mean(y))2=3000,Lxy=∑(x－mean(x))·(y－mean(y))=－1000;则相关系数r=()。注:mean(x)、mean(y)分别为x,y的均值。

A.0.925

B.-0.913

C.0.957

D.0.913

相似考题

1.由12对观测值(xi，yi)，i=1，2，…，12，求得Lxx=238，Lyy=106，Lxy=-153，则下列叙述正确的有( )。A．x与y的相关系数为0.963B．x与y的相关系数为-0.963C．y对x的一元线性回归系数为-1.443D．y对x的一元线性回归系数为-0.643E．x对y的一元线性回归系数为-0.643

2.已知y1(x)和y2(x)是方程y''+p(x)y'+Q(x)y=0的两个线性无关的特解， Y1(x)和Y2 (x)分别是方程y''+p(x)y'+Q(x)y=R1(x)和y''+p(x)y'+Q(x)y=R2(x)的特解。那么方程y''+p(x)y'+Q(x)y=R1(x)y+R2(x)的通解应是： A. c1y1+c2y2B. c1Y1(x)+c2Y2(x) C. c1y1+c2y2+Y1(x) D. c1y1+c2y2+Y1(x)+Y2(x)

3.已知函数y=f(x)在x1和x2处的值分别为y1和y2，其中，x2>x1且x2-x1比较小（例如0.01），则对于（x1，x2）区间内的任意x值，可用线性插值公式（）近似地计算出f(x)的值A.y1+(y2-y1)(x-x1)/(x2-x1) B.x1+(y2-y1)(x-x1)/(x2-x1) C.y2+(y2-y1)(x2-x1)/(x-x1) D.x2+(x2-x1)(x-x1)/(y2-y1)

4.由n个数组(xi，yi。)计算得 Lxx=330，Lxy=-l68，Lyy=9.4 由此可以看出（）。A.x与y，的相关系数r>0B.x与Y的相关系r<0C.Y对x的回归系数b>0D.y对x的回归系数b>0E.相关系数r与回归系数异号

参考答案和解析

参考答案：B

更多“已知Lxx=∑(x－mean(x))2=400,Lyy=∑(y－mean(y))2=3000,Lxy=∑(x－mean(x))·(y－mean(y))=－1000;则相关系数r=()。注:mean(x)、mean(y)分别为x,y的均值。 A.0.925B.-0.913C.0.957D.0.913”相关问题

第1题：

已知x2=x+1，y2=y+1，且x≠y，则x3+y3=______。

答案：
解析：
4。解析：因为x2=x+1，y2 =y+1且x≠y，所以x，y是方程m2=m+1的两个不同的实数根，所以x+y=1，xy=-1，所以x3+y3=(x+y)(x2-xy+y2)=(x+y)[(x+y)2-3xy]=4。
第2题：

在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果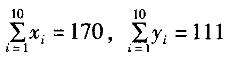：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
X与Y的样本相关系数r为（）。
A. -0.8 B. 0.8 C. 0.64 D. 0.5

答案：B
解析：
相关系数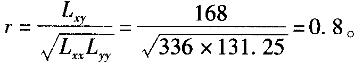
第3题：

在变量Y表示对X进行回归分析时，根据10对观测值(xi,yi), i =1， 2，…10，算得如下结果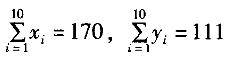：，Lxx=336，Lxy=131.25，Lyy=168。
请回答下列问题。
Y对X的回归系数b为（）。
A. 0.5 B. -0.5 C. 0.582 D. -0.582

答案：A
解析：
设一元线性回归方程的表达式为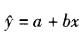：。则根据公式，b=Lxy/Lxx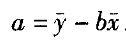，，求得：b=Lxy/Lxx=168/336 =0.5。
第4题：

由 12 对数据（xi，yi）,i = 1，2,…，12，算得 Lxx=165，Lyy=372, Lxy=﹣232，则X与Y间的相关系数r为（）。
A. 0. 936 B. ﹣0. 936
C. 0.875 D. ﹣0. 875

答案：B
解析：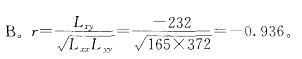
第5题：

x、y两个系列的均值相同，它们的均方差分别为σ_x、σ_y，已知σ_x＞σ_y，说明x系列较y系列的离散程度大。

正确答案:正确
第6题：

已知X和Y，试计算下列各题的[X+Y]补和[X-Y]补（设字长为8位）。（1）X=1011，Y=0011 （2）X=1011，Y=0111 （3）X=1000，Y=1100

正确答案:（1）X补码=00001011，Y补码=00000011，[–Y]补码=11111101，[X+Y]补=00001110，[X-Y]补=00001000
（2）X补码=00001011，Y补码=00000111，[–Y]补码=11111001，[X+Y]补=00010010，[X-Y]补=00000100
（3）X补码=00001000，Y补码=00001100，[–Y]补码=11110100，[X+Y]补=00010100，[X-Y]补=11111100
第7题：

某反应的速率方程为r=k[c（A）]^x[c（B）]^y。当仅c（A）减少50%时，r降低至原来的1/4；当仅c（B）增大到2倍时，r增加到1.41倍；则x，y分别为（）。
- A、x=0.5，y=1
- B、x=2，y=0.7
- C、x=2，y=0.5
- D、x=2，y=1.41
正确答案:C
第8题：

单选题
已知y1（x）与y2（x）是方程y″+P（x）y′+Q（x）y=0的两个线性无关的特解，Y1（x）和Y2（x）分别是是方程y″+P（x）y′+Q（x）y=R1（x）和y″+P（x）y′+Q（x）y=R2（x）的特解。那么方程y″+P（x）y′+Q（x）y=R1（x）+R2（x）的通解应是：（）
A
c1y1+c2y2
B
c1Y1（x）+c2Y2（x）
C
c1y1+c2y2+Y1（x）
D
c1y1+c2y2+Y1（x）+Y2（x）

正确答案： A
解析：暂无解析
第9题：

单选题
已知函数的全微分df（x，y）＝（3x2＋4xy－y2＋1）dx＋（2x2－2xy＋3y2－1）dy，则f（x，y）等于（　　）。
A
x³＋2x²y－xy²＋y³＋x－y＋C
B
x³－2x²y＋xy²－y³＋x－y＋C
C
x³＋2x²y－xy²＋y³－x＋y＋C
D
x³＋2xy²－xy²＋y³＋x－y＋C

正确答案： C
解析：
由题意知∂f/∂x＝3x²＋4xy－y²＋1，两边对x求积分，则f＝∫（∂f/∂x）dx＝x³＋2x²y－xy²＋x＋C（y），∂f/∂y＝2x²－2xy＋C′（y），又因为∂f/∂y＝2x²－2xy＋3y²－1，故C′（y）＝3y²－1，进而有C（y）＝y³－y＋C，f＝x³＋2x²y－xy²＋y³＋x－y＋C。故应选（A）。
第10题：

多选题
设随机变量X1与X2相互独立，它们的均值分别为3与4，方差分别为1与2，则y＝4X1αX2的均值与方差分别为(　　)。
A
E(y)=4
B
E(y)=20
C
Var(y)=14
D
Var(y)=24
E
Var(y)=15

正确答案： A,B
解析： E（y）=4×3-2×4=4Var（y）=16×1+4×2=24
第11题：

问答题
What is the average (arithmetic mean) of x and y?　　(1) The average of x+3 and y+5 is 14.　　(2) The average of x,y and 16 is 12.

正确答案： D
解析：
将两条件分别代入计算可知，x和y的平均数均为10，故本题选D项。
第12题：

问答题
已知y1*＝－x（x＋2）/4，y2*＝（x/10＋13/200）cos2x＋（x/20－2/25）sin2x分别为方程y″－y′＝x/2，y″－y′＝（－xcos2x）/2的特解，求微分方程y″－y′＝xsin2x的通解。

正确答案：
由解的性质可知,y^*=y₁^*+y₂^*是方程y″-y′=xsin²x=x(1-cos2x)/2=x/2-(xcos2x)/2的一个特解,又因为y″-y′=xsin²x对应齐次方程的特征方程r(r-1)=0的根为r₁=0,r₂=1。则该对应齐次方程的通解为y(_)=C₁+C₂e^x。
则方程y″-y′=xsin²x的通解为y=y(_)+y^*=C₁+C₂e^x+(x/10+13/200)cos2x+(x/20-2/25)sin2x-x(x+2)/4。
解析：暂无解析
第13题：

由n个数组（xi，yi)计算得Lxx= 330，_Lxy=﹣168，Lyy= 9.4由此可以看出（）。
A. x与y的相关系数r>0

B.工与y的相关系数r
C. y对x的回归系数b>0

D. y对x的冋归系数b
E.相关系数r与回归系数b异号

答案：B,D
解析：
第14题：

设随机变量X1和X2相互独立，它们的均值分别为3与4，方差分别为1与2，则 Y = 4X1+2X2的均值与方差分别为（）。
A. E (Y) =4 B. E (Y) =20
C.Var (Y) =14 D.Var (Y) =24
E.Var (Y) =15

答案：B,D
解析：
。E (Y) =E(4X1+ 2X2) =4×3 + 2×4 = 20； Var (Y) =Var (4X1 + 2X2 ) =42 × 1 + 22 ×2 = 24。
第15题：

已知y1(X)与y2(x)是方程：y" + P(x)y'+Q(x)y = 0的两个线性无关的特解，y1(x)和y2(x)分别是方程y"+P(x)y'+Q(x)y=R1(x)和y"+p(x)+Q(x)y=R2(x)的特解。那么方程y"+p(x)y'+Q(x)y=R1(x)+R2(x)的通解应是：

A. c1y1+c2y2
B. c1Y1(x) +c2Y2 (x)
C. c1y1+c2y2 +Y1(x)
D. c1y1+c2y2 +Y1 (x) +Y2 (x)

答案：D
解析：
提示：按二阶线性非齐次方程通解的结构，写出对应二阶线性齐次方程的通解和非齐次方程的一个特解，得到非齐次方程的通解。
第16题：

由n个数组(xi,yi)计算得Lxx= 330, Lxy =-168,Lxy=9.4由此可以看出（）。

A. X与y，的相关系数r>0
B. X与y的相关系数rC. y与x对r的回归系数b>0
D. y对x的回归系数bE.相关系数r与回归系数异号

答案：B,D
解析：
第17题：

在回归和相关分析中，lyy表示（）.
- A、∑（x-y）
- B、∑（y-y）
- C、∑（x-x）2
- D、∑（y-y）2
- E、∑（x-x）（y-y）
正确答案:D
第18题：

设随机变量X和Y的相关系数为0.5，E（X）=E（Y）=0，E（X²）=E（Y²）=2，则E（X+Y）²=（）。

正确答案:6
第19题：

单选题
已知y＝x/lnx是微分方程y′＝y/x＋φ（x/y）的解，则φ（x/y）的表达式为（　　）。
A
－y²/x²
B
y²/x²
C
－x²/y²
D
x²/y²

正确答案： B
解析：
将y＝x/lnx代入微分方程得（lnx－1）/ln²x＝1/lnx＋φ（x/y）。故φ（x/y）＝－1/ln²x＝－1/（x/y）²＝－y²/x²。
第20题：

多选题
设随机变量X1与X2相互独立，它们的均值分别为3与4，方差分别为1与2，则Y=4X1-2X2的均值与方差分别为（　　）。
A
E（Y）=4
B
E（Y）=20
C
Var（Y）=8
D
Var（Y）=14
E
Var（Y）=24

正确答案： B,A
解析：
E（Y）=E（4X₁-2X₂）=4E（X₁）-2E（X₂）=4×3－2×4=4；
Var（Y）=Var（4X₁-2X₂）=4²Var（X₁）+（－2）²Var（X₂）=16×1+4×2=24。
第21题：

单选题
被测量Y与输入量X1、X2、X3的估计值分别为y、x1、x2和x3,它们之间的函数关系为y=2X1+2X2+10X3，，已知如果各输入量之间的相关系数均为1，则被测量Y的合成标准不确定度uc（y）是（）。
A
0.03
B
0.09
C
0.12
D
0.36

正确答案： B
解析：
第22题：

单选题
The average (arithmetic mean) of x and y is m, where m ≠ 0. What is the average (arithmetic mean) of x, y, and 2m?
A
m
B
4/3m
C
3/2m
D
5/3m
E
2m

正确答案： D
解析：
因为x和y的算术平均数为m，所以x+y=2m，所以，所以x,y,2m的算术平均数为x+y+2m/3，因为x + y = 2m，所以x+y+2m/3=4m/3
第23题：

单选题
在回归和相关分析中，lyy表示（）.
A
∑（x-y）
B
∑（y-y）
C
∑（x-x）2
D
∑（y-y）2
E
∑（x-x）（y-y）

正确答案： E
解析：暂无解析

已知Lxx=∑(x－mean(x))2=400,Lyy=∑(y－mean(y))2=3000,Lxy=∑(x－mean(x))·(y－mean(y))=－1000;则相关系数r=()。注:mean(x)、mean(y)分别为x,y的均值。A.0.925B.-0.913C.0.957D.0.913

题目

相似考题

参考答案和解析

更多“已知Lxx=∑(x－mean(x))2=400,Lyy=∑(y－mean(y))2=3000,Lxy=∑(x－mean(x))·(y－mean(y))=－1000;则相关系数r=()。注:mean(x)、mean(y)分别为x,y的均值。 A.0.925B.-0.913C.0.957D.0.913”相关问题

相关内容