高一三个班举行年级运动会，设跳高、跳远和百米三项，各项均取前三名，第一名5分，第二名3分，第三名1分。已知一、二班总分相等，并列第一名，而二班进入前三名的人数是一班的两倍，那么三班总分是多少分?（ ）A．5B．6C．7D．8

题目

高一三个班举行年级运动会，设跳高、跳远和百米三项，各项均取前三名，第一名5分，第二名3分，第三名1分。已知一、二班总分相等，并列第一名，而二班进入前三名的人数是一班的两倍，那么三班总分是多少分?（ ）

A．5

B．6

C．7

D．8

相似考题

1.六年级三个班参加运动会，运动会上举行三个项目的比赛。第一名得5分，第二名得3分，第三名得1分。已知(1)班进入前三名的人数最少，(2)班进入前3名的人数是(1)班的2倍，且这两个班所得总分相等，并列年级组的第一名。(3)班得了（ ）分。A．9B．8C．7D．6

2.某班45名同学参加了体育测试，其中百米得优者20人，跳远得优者18人。又知百米、跳远均得优者7人、跳高、百米均得优者6人，跳高、跳远均得优者8人，跳高得优者22人，全班只有l名同学各项都没达到优，求三项都是优的人数。（ ）A．3B．4C．5D．6

3.高一三个班举行年级运动会，设跳高、跳远和百米三项，各项均取前三名，第一名5分，第二名3分，第三名1分．已知一、二班总分相等，并列第一名，而二班进入前三名的人数是一班的两倍，那么三班总分是多少分？()A．5B．6C．7D．8

4.高一三个班举行年级运动会，设跳高、跳远和百米三项，各项均取前三名，第一名5分。第二名3分，第三名1分。已知一、二班总分相等，并列第一名，而二班进入前三名的人数是一班的两倍，那么三班总分是多少分?（ ）A．5B．6C．7D．8

参考答案和解析
正确答案：C
三项均取前三名，那么一共有9人进入前三名，由于二班进入前三名的人数是一班的两倍，可以有二班和一班的人数可以为2和1，4和2，6和3。假如是2和1，那么三班将有6人，无论如何三班得分都不会排在最后，首先排除；假如是6和3，一、二班总分无法相等，也排除这种情况；只能是二班4人，一班2人，三班3人。进入前三名的总分为(5＋3＋1)×3＝27，也就是说一、二班的得分至少应有10分，而一班的两个人得分最多的情况是二人都得第一名共得10分，所以一、二班的得分均为10分，那么三班的得分为27－10－10＝7(分)，故选C。
更多“高一三个班举行年级运动会,设跳高、跳远和百米三项,各项均取前三名,第一名5分,第二名3分 ”相关问题

  • 第1题：

    共有4人进行跳远、百米、铅球、跳高4项比赛，规定每个单项中，第一名记5分，第二名记3分，第三名记2分，第四名记1分。已知在每一单项比赛中都没有并列名次，并且总分第一名共获17分，其中跳高得分低于其他项得分；总分第三名共获11分，其中跳高得分高于其他项得分。问总分第二名哪个项目得了第一名?（ ） A．跳高 B．百米 C．铅球 D．没有哪个项目得第一名


    正确答案：D
    每个单项的4人共得分5+3+2+1＝11分，所以4个单项的总分为11×4＝44分，而第一、三名得分分别为17、11分，所以第二、四名得分之和为44－(17+11) ＝16分，其中第四名得分最少为1×4＝4分，所以第二名得分最高为16－4＝12分；又因为第三名为11分，所以第二名最低为12分，那么第二名只能为12分，此时第四名得4分。不难得到下表。

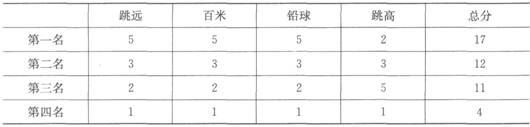
    故总分第二名没有哪个项目得第一名。故选D。

  • 第2题：

    六年级三个班参加运动会，运动会上举行三个项目的比赛。第一名得5分，第二名得3 分，第三名得1分。已知（1)班进入前三名的人数最少，（2)班进入前3名的人数是（1)班 的2倍。且这两个班所得总分相等，并列年级组的第一名。（3)班得了（ ）分。
    A. 9 B. 8 C. 7 D. 6


    答案：C
    解析：
    (1)班得名次的如果是3人，则（2)班需有6人得名次，但这样一来全部9个名次均被两个班瓜分，却无法产生并列第一名。全部得分3×(1+ 3 + 5)=27是奇数，因此 (1)班至多只有两人得名次，而两人得名次且只能都拿第一名才能满足与（2)班并列第一的要求。若有一人拿第二，则只能拿8分，而这不超过平均分27 + 3 = 9(分），无法并列第一。据此，（1)班和（2)班各得10分，（3)班必然得27-10×2 = 7(分）。

  • 第3题：

    六年级三个班参加运动会，运动会上举行三个项目的比赛。第一名得5分，第二名得3 分，第三名得1分。已知（1)班进人前三名的人数最少，（2)班进人前3名的人数是（1)班 的2倍。且这两个班所得总分相等，并列年级组的第一名。（3)班得了（ ）分。
    A. 9 B. 8 C. 7 D. 6


    答案：C
    解析：
    (1)班得名次的如果是3人，则（2)班需有6人得名次，但这样一来全部9 个名次均被两个班瓜分，却无法产生并列第一名。全部得分3 X (1 + 3 + 5) = 27是奇数，因此 (1)班至多只有两人得名次，而两人得名次且只能都拿第一名才能满足与（2)班并列第一的要 求。若有一人拿第二，则只能拿8分，而这不超过平均分27÷3 = 9(分），无法并列第一。据 此，（1)班和（2)班各得10分，（3)班必然得27 — 10X2 = 7(分）。

  • 第4题：

    某班45名同学参加了体育测试，其中百米得优者20人，跳远得优者18人，又知百米、跳远均得优者7人，跳高、百米均得优者6人，跳高、跳远均得优者8人，跳高得优者22人，全班只有1名同学各项都没有达到优，则三项都是优的人数为（ ）。 A．3人 B．4人 C．5人 D．6人


    正确答案：C
    根据题意，设三项都是优的人数为x人，则由容斥原理可得，20+18+22－(7+6+8)+x＝45－1，解得x＝5。故选C。

  • 第5题：

    校运会跳高、跳远、百米跨栏三个项目共有68名同学报名参加，其中报名跳高的有24人，跳远的有29人，百米跨栏的有35人，已知有2个人三个项目都报名了，则只参加了一个项目的学生有( )人。

    A.20
    B.16
    C.35
    D.50

    答案：D
    解析：
    根据三集合非标准型公式，总数-A+B+C-满足两条件-2ABC+非ABC,则根据题意可得68-24+29+35-满足两条件-2X2,解得“满足两条件”-16，则只参加一个项目的学生=68-参加两个项目的-参加三个项目的-68-16-2=50人，D选项正确，A. B、C选项错误。故本题应选D.

相关内容