某校参加数学竞赛的有 120 名男生,80 名女生,参加语文的有 120 名女生,80 名男生。已知该校总共有 260名学生参加了竞赛,其中有 75 名男生两科都参加了,问只参加数学竞赛而没有参加语文的女生有多少人?( )A.65 人B.60 人C.45 人D.15 人
题目
某校参加数学竞赛的有 120 名男生,80 名女生,参加语文的有 120 名女生,80 名男
生。已知该校总共有 260名学生参加了竞赛,其中有 75 名男生两科都参加了,问只参加数学
竞赛而没有参加语文的女生有多少人?( )
A.65 人
B.60 人
C.45 人
D.15 人
相似考题
更多“某校参加数学竞赛的有 120 名男生,80 名女生,参加语文的有 120 名女生,80 名男生。已知该校总 ”相关问题
-
第1题:
某大学外语系选修西班牙语的有20名男生,160名女生,选修葡萄牙语的有120名女生,10名男生,已知该系总共有260名学生选修了这两种语言,其中有5名男生两种语言都选修了,只选修了西班牙语而没有选修葡萄牙语的女生有多少人?( )
A.85
8.90
C.145
D.115
正确答案:D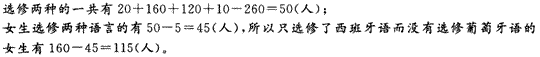
-
第2题:
某校有 58 名同学参加数学竞赛,已知将参赛人任意分成四组,则必有一组的女生多于3 人,又知参赛者中任意 14 人中必有男生,则参赛男生的人数为:
A.45
B.46
C.47
D.48答案:A解析:由题干中必有一组女生多于3人,根据最不利原则可知,四组女生最少人数为3×4+1=13人,而又根据任意14人中必有男生得知,女生人数不超过13人,则可确定女生人数就是13人。总人数为58人,男生45人,所以选择A。 -
第3题:
—次校友聚会共有50人参加,在参加聚会的同学中,每个男生认识的女生人数各不相同,而且恰好构成一串连续的自然数。已知认识女生最少的一个男生认识15名女生,并有一名男生认识所有女生,则参加这次聚会的男生一共有:A.16 名
B.17 名
C.18 名
D.19 名答案:C解析:设共有x名男生,则有女生50-x名,认识女生最多的一名男生认识x-1+15名女生,则有x-1+15=50-x,解得x=18。 -
第4题:
某校有58名同学参加数学竞赛,已知将参赛人任意分成四组,则必有一组的女生多于3人,又知参赛者中任意14人中必有男生,则参赛男生的人数为:
A45
B46
C47
D48答案:A解析:
-
第5题:
某校参加数学竞赛的有l20名男生.80名女生,参加语文竞赛的有l20名女生,80名男生。已知该校总共有260名学生参加了竞赛,其中有75.名男生两科都参加了,则只参加数学竞赛而没有参加语文竞赛的女生有( )。
A. 65人
B. 60人
C. 45人
D. 15人答案:D解析:共有(120+80)×2—260=140人同时参加两科竞赛,其中女生人数是140—75=65人。那么只参加数学竞赛的女生有80—65=l5人。
