把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。A．73280cm2B．54680cm2C．69450cm2D．46080cm2
题目
把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（ ）。
A．73280cm2
B．54680cm2
C．69450cm2
D．46080cm2
相似考题
更多“把一个64Cmx40Cmx24Cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积 ”相关问题
-
第1题：
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为( )。
A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2
正确答案：D
解析：要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为8，因此小正方体的边长为8cm，共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2。 -
第2题：
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体，并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（)。A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2答案：D解析：要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大.64、40、24的最大公约数为8，因此小正方体的边长为8cm,共有64×40×24÷83=l20块。表面积总和为6×82×120=46080cm2. -
第3题：
将一个8厘米×8厘米×1厘米的白色长方体木块的外表面涂上黑色颜料，然后将其切成64个棱长1厘米的小正方体，再用这些小正方体堆成棱长4厘米的大正方体，且使黑色的面向外露的面积要尽量大，问大正方体的表面上有多少平方厘米是黑色的？A. 88
B. 84
C. 96
D. 92答案：A解析：白色长方体可以看做64个小正方体平铺，由4个角，24个棱和36个中间小正方体构成，角上的4个小正方体有4个面被刷成了黑色，棱上的24个小正方体连续的3个面被刷成了黑色，中间的36个小正方体相对的2个面被刷成了黑色；拼成的大正方体有8个角，24个棱和24个单面，拼接时有4个角需用之前棱上的小正方体替换，每替换一次缺一个黑色面，角上共缺了4个；由于4个棱上的正方体替换到了角上，此时棱上又少了4个小正方体，需用对面为黑色的小正方体替换，每替换一次缺一个黑色面，棱上共缺了4个。大正方体的表面积为4×4×6=96平方厘米，大正方体的表面上共有96-4-4=88平方厘米是黑色的。因此，本题选A。 -
第4题：
用n个棱长是a cm的小正方体可以摆出“一”字形长方体，如图，n个小正方体拼在一起 时，这个长方体表面积是_______cm2。
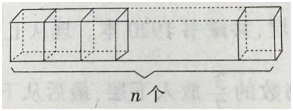答案：解析：(4n+2)a2。解析:n个小正方体如题干图中所示拼在一起时，组成长为na，宽为a，高为a的长方体，所以表面积为(4n+2)a2 cm2。 -
第5题：
把一个64cm×40cm×24cm的长方体切成若干个完全相同的小正方体,并使这些小正方体的表面积总和最小，则小正方体的表面积总和为（）。A.73280cm2
B.54680cm2
C.69450cm2
D.46080cm2答案：D解析：要使这些小正方体的表面积总和最小，那么小正方体的边长要尽可能大。64、40、24的最大公约数为8,因此小正方体的边长为8cm,共有64×40×24÷83=120块。表面积总和为6×82×120=46080cm2.