要折叠一批纸飞机，若甲单独折叠要半个小时完成，乙单独折叠需要45分钟完成。若两人一起折，需要多少分钟完成?A．10B．15C．16D．18

题目

要折叠一批纸飞机，若甲单独折叠要半个小时完成，乙单独折叠需要45分钟完成。若两人一起折，需要多少分钟完成?

A．10

B．15

C．16

D．18

相似考题

1.要折叠一批纸飞机，若甲单独折叠要半个小时完成，乙单独折叠需要45分钟完成。若两人一起折，需要多少分钟完成？（ ） 。A．10B．15C．16D．18

2.一件工程,甲乙两人合作36小时完成,乙丙两人合作45小时完成,甲丙两人合作要60小时完成,问甲单一件工程，甲乙两人合作３６小时完成，乙丙两人合作45小时完成，甲丙两人合作要60小时完成，问甲单独做需要多少小时完成？A.72B.75C.81D.90

3.要折叠一批纸飞机.若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要多少分钟完成?A.10 B.15 C.16 D.18

4.一篇文章，现有甲乙丙三人，如果由甲乙两人合作翻译，需要10小时完成，如果由乙丙两人合作翻译，需要12小时完成。现在先由甲丙两人合作翻译4小时，剩下的再由乙单独去翻译，需要12小时才能完成，则这篇文章如果全部由乙单独翻译，要（　　　　）小时完成。A.15　　　　B.18　　　　C.20　　　　D.251

更多“要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成。若两人一起折,需要多少 ”相关问题

  • 第1题：

    某公司要完成一项工程，如果单独交给甲项目组，需要x天完成；如果单独交给乙项目组，需要y天完成，若甲、乙两个项目组共同完成该项目，最短需要多少天？



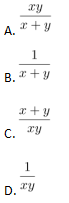    答案：A
    解析：
    第一步，本题考查工程问题，属于时间类，用赋值法解题。
    第二步，赋值工程总量为x、y的最小公倍数xy，则甲的效率为xy÷x＝y，乙的效率为xy÷y＝x，则两人一起合作需要

  • 第2题：

    一项工程甲、乙、丙一起来做，已知若甲、乙两人一起做则15天可以完成，若乙、丙两人一起做18天可以完成。已知在甲、乙、丙一起做这项工程的过程中，乙因事请假2天，结果共用10天恰好完成。那么这项工程若由乙单独做，要多少天完成？（ ）

    A. 36
    B. 48
    C. 54
    D. 56

    答案：C
    解析：
    本题可采用方程法。设整个工程的工作量为1，甲、乙、丙每天的工作量分别为x、y、z。根据题意可得：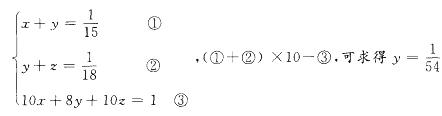

    即若乙单独做这项工程需要54天。

  • 第3题：

    有甲、乙两项工程，张师傅单独完成甲工程需要9天，单独完成乙工程需要12天；王师傅单独完成甲工程需要3天，单独完成乙工程需要15天。如果两人合作完成这两项工程，最少需要多少天？（ ）
    A. 8 B. 10 C. 12 D. 14


    答案：A
    解析：
    王先做甲工程，张先做乙工程，然后再合作。

  • 第4题：

    一件工程，甲乙两人合作３６小时完成，乙丙两人合作45小时完成，甲丙两人合作要60小时完成，问甲单独做需要多少小时完成？

    A.72
    B.75
    C.81
    D.90

    答案：D
    解析：
    我们设总的工作量是天数的最小公倍数，即180（36、45、60的最小公倍数），同时，设甲乙丙的工作效率分别是XYZ。题目说“甲乙两人合作36天完成”，说明甲乙合作一天的效率就是5（180÷36），根据“乙丙两人合作45天完成”，说明乙丙合作一天的效率就是4（180÷45），根据“甲丙两人合作要60天完成”，说明甲丙合作一天的效率就是3（180÷60）。所以可以列方程：
    X＋Y＝5，Y＋Z＝4，X＋Z＝3
    解方程得：X＝2，也就是甲单独做的工作效率是2，那么已知总的工作量为180，所以甲独 做需要90（180÷2）天完成。

  • 第5题：

    一项工程甲、乙、丙一起来做，已知若甲、乙两人一起做则15天可以完成，若乙、丙两人一 起做18天可以完成。已知在甲、乙、丙一起做这项工程的过程中，乙因事请假2天，结果 共用10天恰好完成。那么这项工程若由乙单独做,要多少天完成？（ ）


    A. 36 B. 48 C. 54 D. 56


    答案：C
    解析：
    C [解析]本题可采用方程法。设整个工程的工作量为1，甲、乙、丙每天的工作量分

相关内容