甲、乙、丙三人,两年后甲的年龄比乙的年龄的2倍还大3岁,一年前乙的年龄比丙的年龄的2倍小2岁,三个人的年龄之和是108岁,则三年后甲的年龄比乙大( )岁。 A.33 B.34 C.36 D.37
题目
甲、乙、丙三人,两年后甲的年龄比乙的年龄的2倍还大3岁,一年前乙的年龄比丙的年龄的2倍小2岁,三个人的年龄之和是108岁,则三年后甲的年龄比乙大( )岁。 A.33 B.34 C.36 D.37
相似考题
参考答案和解析
正确答案:B
设甲、乙、丙的年龄分别为x、y、z,可得
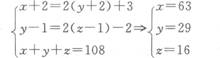
两人的年龄差保持不变,故三年后甲的年龄比乙大63—29=34(岁),故选B。
设甲、乙、丙的年龄分别为x、y、z,可得
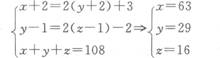
两人的年龄差保持不变,故三年后甲的年龄比乙大63—29=34(岁),故选B。
更多“甲、乙、丙三人,两年后甲的年龄比乙的年龄的2倍还大3岁,一年前乙的年龄比丙的年龄的2倍小2岁,三个 ”相关问题
-
第1题:
甲乙丙三人的平均年龄是25岁,已知甲是乙的年龄的2倍少7岁,丙比甲的年龄小1岁,问甲的年龄是多少?( )
A.29
B.30
C.25
D.35
正确答案:A
假设乙的年龄是X岁,则甲为2x-7,丙为2x-8,所以有x+(2x-7)+(2x-8)=25×3,可以得到x=18,2x-7=29岁。 -
第2题:
甲2018年的年龄比乙的2倍大3岁,3年后乙的年龄是丙年龄的3倍小7岁。已知丙出生时甲31岁,问哪一年三人的年龄和第一次超过100岁?( )A.2029
B.2030
C.2031
D.2032答案:D解析:第一步,本题考查年龄问题。
第二步,设三年后丙的年龄为x,列表:

第三步,由丙出生时甲31岁可知二人相差31岁,有2×(3x-10)+3-(x-3)=31,解得x=9,则2018年甲、乙、丙三人年龄分别为37、17、6岁,年龄和为37+17+6=60,每过一年每人都长一岁,则每过一年三人年龄和长3岁,在14年后三人年龄和为60+3×14=102(岁),即第一次超过100岁,2018年再过14年为2018+14=2032年。 -
第3题:
体育馆内正进行一场乒乓球双打比赛,观众议论双方运动员甲、乙、丙、丁的年龄:
(1)“乙比甲的年龄大。”
(2)“甲比他的伙伴的年龄大。”
(3)“丙比他的两个对手的年龄都大。”
(4)“甲与乙的年龄差距比丙与乙的年龄差距更大些。”
根据这些议论,甲、乙、丙、丁的年龄从大到小的顺序是( )。A.甲、丙、乙、丁
B.丙、乙、甲、丁
C.乙、甲、丁、丙
D.乙、丙、甲、丁答案:D解析:第四个,用排除法
(1)“乙比甲的年龄大。”
把A排了
(3)“丙比他的两个对手的年龄都大。”
把c排了
(4)“甲与乙的年龄差距比丙与乙的年龄差距更大些。”
把b排了 -
第4题:
有老师和甲、乙、丙三个学生,现在老师的年龄刚好是三个学生的年龄和;9年后,老师年龄为甲、乙两个学生的年龄和;又3年后,老师年龄为甲、丙两个学生的年龄和;再3年后,老师年龄为乙、丙两个学生的年龄和。那么老师现在的年龄是( )岁。
A.33
B.35
C.36
D.39
正确答案:
老师=甲+乙+丙,老师+9=甲+9+乙+9,比较一下这两个条件,很快得到丙的年龄是9岁;老师+9+3=甲+9+3+丙+9+3,老师+9+3+3=乙+9+3+3+丙+9+3+3得到乙是9+3=12岁,甲是9+3+3=15岁。老师是9+12+15=36岁。
-
第5题:
某学校甲、乙、丙三位老师年龄各不相同,一位喜欢足球,一位喜欢篮球,一位喜欢排球。现在知道:甲比喜欢足球的人年龄大;喜欢排球的老师比喜欢篮球的老师年龄小;乙老师年龄最大。
由此可以推出:
A甲老师年龄最小
B乙老师喜欢排球
C丙老师喜欢足球
D三人年龄大小无法确定答案:C解析:第一步:找突破口。
根据题干信息,按年龄大小排列,①乙年龄最大,②甲>喜欢足球的人,③喜欢篮球的人>喜欢排球的人,从“乙年龄最大”和“甲>喜欢足球的人”可知,“乙>甲>喜欢足球的人”,因此喜欢足球的人是丙,且丙的年龄最小。
第二步:结合其他信息进行推导,得出答案。
由题干已知信息,“喜欢篮球的人>喜欢排球的人”,因此喜欢篮球的人是乙,喜欢排球的人是甲。
故正确答案为C。
