一艘游轮从甲港口顺水航行至乙港口需7小时，从乙港口逆水航行至甲港口需9小时。问如果在静水条件下，游轮从甲港口航行至乙港口需多少小时？A．7.75小时B．7.875小时C．8小时D．8.25小时

题目

一艘游轮从甲港口顺水航行至乙港口需7小时，从乙港口逆水航行至甲港口需9小时。问如果在静水条件下，游轮从甲港口航行至乙港口需多少小时？

A．7.75小时

B．7.875小时

C．8小时

D．8.25小时

相似考题

1.甲、乙两人沿直线从A地步行至B地，丙从B地步行至A地。已知甲、乙、丙三人同时出发，甲和丙相遇后5分钟，乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问AB两地的距离为多少米?

2.甲、乙两个港口相距120千米，船从甲到乙顺水航行需要5小时，从乙到甲逆水航行需要20小时。现有A、B两条船分别从甲、乙两港同时出发，相向而行，5小时后C船从甲港出发驶往乙港，则A、B相遇后（ ）小时，B、C相遇。A．6.5B．5.2C．4D．3

3.甲、乙两人沿直线从A地步行至B地，丙从B地步行至A地。已知甲、乙、丙三个同时出发，甲和丙相遇后5分钟，乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问AB两地距离为多少米？A、8000米 B、8500米 C、10000米 D、10500米

4.两港口相距450千米，甲船行全程需用15小时，乙船行全程需12小时。甲船因事先出发2小时，后乙去追甲，乙要走（ ）千米才能追上甲。A．300B．255C．240D．150

更多“一艘游轮从甲港口顺水航行至乙港口需7小时,从乙港口逆水航行至甲港口需9小时。问如果在 ”相关问题

  • 第1题：

    一个港口每年从水运转陆运和从陆运转水运的货物数量总和，称为()。

    A、港口通过能力

    B、港口容量

    C、港口转运量

    D、港口吞吐量


    参考答案：D

  • 第2题：

    甲、乙两船静水速度分别为60米／分钟和40米／分钟，现在两船同时分别从A、B两港口出发相向而行，甲船顺水，乙船逆水，经IO分钟后两船相遇，相遇地点离A、B两地的中点120米。求水的流速是多少米／分钟？

    A．1

    B．2

    C．3

    D．4


    正确答案：B

  • 第3题：

    某旅游部门规划一条从甲景点到乙景点的旅游线路，经测试，旅游船从甲到乙顺水匀速行驶需3小时；从乙返回甲逆水匀速行驶需4小时。假设水流速度恒定，甲乙之间的距离为y公里，旅游船在静水中匀速行驶y公里需要x小时，则x满足的方程为( )


    答案：A
    解析：

  • 第4题：

    A,B两个港口相距300千米,若甲船顺水自A驶向B,乙船同时自B逆水驶向A,两船在C处相遇,若乙船顺水自A驶向B,甲船同时自B道水驶向A,两船在D处相遇.C,D相距30千米,已知甲船速度为27千米/小时,则乙船的速度为（ ）千米/小时

    A.243/11
    B.33
    C.33或243/11
    D.32
    E.34

    答案：C
    解析：

  • 第5题：

    长江中游有甲、乙两港，相距360千米。一艘轮船从甲港到乙港，顺水航行15小时到达，从乙港返回甲港，逆水航行20小时到达。现有一艘小艇，航速是每小时32千米，它往返两港需要（　　）小时。

    A.15
    B.18
    C.23
    D.28

    答案：C
    解析：

  • 第6题：

    甲、乙因港口作业中发生纠纷，甲欲通过诉讼方式解决。下列关于其选择诉讼管辖法院的表述中，符合法律规定的是（　）。

    A.甲只能向甲住所地法院提起诉讼
    B.甲只能向乙住所地法院提起诉讼
    C.甲只能向港口所在地法院提起诉讼
    D.甲可以选择向乙住所地或港口所在地法院提起诉讼

    答案：C
    解析：
    根据规定，因港口作业中发生纠纷提起的诉讼，由港口所在地法院管辖。

  • 第7题：

    《汉堡规则》规定，将承运人的责任期间从装船至卸船改为从港口到港口。


    正确答案:正确

  • 第8题：

    船舶在港口需进行明火作业时，必须向本港口海事部门报备.


    正确答案:正确

  • 第9题：

    甲、乙两艘船完工日期均为2012.8.15，两艘船航行在同一港口同时安检，发现货舱区舷舱空气管未装关闭装置。结果甲船放行，乙船被滞留。可能是下列什么原因？（）

    • A、甲船安放龙骨时间在2011年9月1日之前，乙船安放龙骨时间在2011年9月1日或之后
    • B、甲船为B级航区，乙船为A级航区
    • C、乙船安放龙骨时间在2011年9月1日之前，甲船安放龙骨时间在2011年9月1日或之后
    • D、乙船为B级航区，甲船为A级航区

    正确答案:A

  • 第10题：

    国内港口的费收化分为北方沿海、南方沿海、长江、珠江等航区。


    正确答案:错误

  • 第11题：

    多选题
    三峡库区巫山县大宁河以巫山龙门大桥为界上游为C级航区、下游为B级航区，上游C级航区有大昌客运港口、下游B级航区有巫山客运港口，能航运于两港口间的客班船其船舶检验证书核定航区可以为（）
    A

    A级

    B

    B级

    C

    C级

    D

    J1级


    正确答案： A,C
    解析： 暂无解析

  • 第12题：

    单选题
    布局规划、主要港口和地区性重要港口的总体规划（包括专项规划和控制性详细规划）需持有港口河海工程专业（）级咨询资质或水运行业（）级设计资质的单位承担。
    A

    甲；甲

    B

    乙；乙

    C

    特；特


    正确答案： B
    解析： 暂无解析

  • 第13题：

    一只游轮从甲港顺流而下到乙港，马上又逆水返回甲港，共用8小时，顺水每小时比逆水每小时多行12千米，前4小时比后4小时多行30千米。甲、乙两港相距多少千米？

    A.72B.60C.55D.48

  • 第14题：

    一艘船往返于甲乙两港口之间，已知水速为8千米/时，该船从甲到乙需要6小时，从乙返回甲需9小时，问甲乙两港口的距离为多少千米：
    A216
    B256
    C288
    D196


    答案：C
    解析：

  • 第15题：

    下图为美国，加拿大部分港口分布示意图，读图完成第下题。



    甲乙丙三个港口封冻期由长到短排序正确的是（ ）。

    A.乙＞丙＞甲
    B.丙＞乙＞甲
    C.乙＞甲＞丙
    D.甲＞乙＞丙

    答案：A
    解析：
    从相同纬度来看，海港的结冰期要比淡水港口的结冰期短，且甲海港受沿岸暖流的影响，所以甲结冰期最短，乙地纬度比丙地高，乙地结冰期较长，所以三地结冰期从长到短为：乙＞丙＞甲，故选A。

  • 第16题：

    —艘巡逻艇航行至海面某处时，得知正北方向20海里处有一渔船发生故障，就立即指挥港口的救援艇前往该处营救。已知发生事故处位于港口北偏东45°的方向上，港口位于巡逻 艇北偏西30°的方向上。港口到出事地点的距离为：


    答案：B
    解析：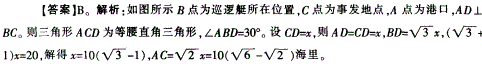

  • 第17题：

    某旅游部门规划一条从甲景点到乙景点的旅游线路，经测试，旅游船从甲到乙顺水匀速行驶需3小时；从乙返回甲逆水匀速行驶需4小时，假设水流速度恒定，甲乙之间的距离为 y公里，旅游船在静水中匀速行驶y 公里需 x小时，则X满足 的方程式为（ ）


    答案：D
    解析：
    【思路点拨】选择 D中所列方程1/3-1/x=1/x-1/4有等量关系，即
    顺水速度-静水速度=静水速度-逆水速度 相当于水速=水速，有等量关系，故应选择D选项。

  • 第18题：

    世界港口发展大体经历三代 ，第一代港口主要是（）、（）；第二代港口除了货物的装卸、仓储外 ，还增加了工业、商业活动，使港口成为具有使货物增值效应的服务中心；第三代港口适应国际经济、贸易、航运和物流发展的要求，得益于港航信息技术的发展，使港口逐步走向国际物流中心。


    正确答案:海运货物的装卸；仓储中心

  • 第19题：

    有些港口由于拥挤，致使船舶停泊时间增加而加收的附加费是指（）。

    • A、港口附加费
    • B、绕航附加费
    • C、转船附加费
    • D、港口拥挤附加费

    正确答案:D

  • 第20题：

    位于两个航区分界处，如其属较高级别的航区内的港口，对航行低一级别航区的船舶进出该港口，可作为何航区航行的船舶？（）

    • A、航行于较高级别区域
    • B、航行于较低级别区域
    • C、对船舶重新核定
    • D、无明确的规定

    正确答案:B

  • 第21题：

    根据《国际防止海上油污公约》和《国际防止船舶污染公约》的规定，下列关于对船舶污染海洋的责任和管辖制度表述正确的是：（　）

    • A、甲国是船舶乙的船旗国，对于乙的污染行为甲国享有调查并提起诉讼的权利
    • B、乙国的船舶在甲国的管辖范围内的违章行为，甲国有管辖权
    • C、乙国的船舶在丙国的港口违反了丙国的法律，在进入甲国港口后，根据公约的规定，甲国应在实际可行的范围内满足丙国对乙国船舶进行调查的请求
    • D、乙国的船舶在丙国的港口违反了丙国的法律，在进入甲国港口后，根据公约的规定，甲国应在实际可行的范围内满足乙国对船舶要求调查的请求

    正确答案:A,B,C,D

  • 第22题：

    单选题
    有些港口由于拥挤，致使船舶停泊时间增加而加收的附加费是指（）。
    A

    港口附加费

    B

    绕航附加费

    C

    转船附加费

    D

    港口拥挤附加费


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    一艘游轮从甲港口顺水航行至乙港口需7小时，从乙港口逆水航行至甲港口需9小时。如果在静水条件下，游轮从甲港口航行至乙港口需多少小时？（　　）
    A

    7.75

    B

    7.875

    C

    8

    D

    8.25


    正确答案： D
    解析：
    设甲乙港口的距离为63，则顺水、逆水的速度分别为9、7，船自身的速度为（9＋7）÷2＝8，因此在静水条件下从甲港口航行至乙港口所需时间为63÷8＝7.875小时。

相关内容