原计划在雕塑周围用若干盆花围成一个4层的空心方阵,但为了整体美观,最后决定将花盆排成2层。4层空心方阵与2层空心方阵相比,最外一层每边少8盆,那么一共有多少盆花?( )A.120盆B.146盆C.160盆D.164盆
题目
原计划在雕塑周围用若干盆花围成一个4层的空心方阵,但为了整体美观,最后决定将花盆排成2层。4层空心方阵与2层空心方阵相比,最外一层每边少8盆,那么一共有多少盆花?( )
A.120盆
B.146盆
C.160盆
D.164盆
相似考题
更多“原计划在雕塑周围用若干盆花围成一个4层的空心方阵,但为了整体美观,最后决定将花盆排成2层。4 ”相关问题
-
第1题:
现有鲜花若干盆,若用它们排成3层空心方阵,则多出5盆;若在中间再增加一层,则少11盆,则现有鲜花( )盆。
A.101
B.105
C.108
D.112
正确答案:A
设最内层有鲜花X盆,则共有鲜花[x+(x+8)+(x+8×2)+5]盆或[x+ (X+8)+(X+8×2)+(x-8)=11]盆,根据题意可得: x+(X+8)+(X+8×2)+5=X+(X+8)+(X+8×2)+(x-8)-11→x=24
故现有鲜花24+(24+8)+(24+8×2)+5=101(盆),A项正确。 -
第2题:
200人排成一个5层的空心方阵,那么方阵最外层人数为( )人。
A. 17 B. 56 C. 15 D. 58答案:B解析:方阵中从外到内每达的人数依次递减2人,设最外一层每达人数为X人, 那么空心部分每边人数应为(x—10),根据题意可知:X 2— (x—10) 2=200,解得X= 15,即方阵 最外层每达人数为15人,那么最外层一共有4X15 — 4 = 56(人)。答案为B。 -
第3题:
200人排成一个5层的空心方阵,那么方阵最外层人数为( )人。
A. 17 . 56 C. 15 D. 58答案:B解析:方阵中从外到内每边的人数依次递减2人,设最外一层每边人数为x人, 那么空心部分每边人数应为(x-10),根据题意可知:x2 -(x-10)2 =200,解得x=15,即方阵最外层每边人数为15人,那么最外层一共有4×15 -4 = 56(人)。答案为B。 -
第4题:
园丁将若干同样大小的花盆在平地上摆放为不同的几何图形,发现如果增加5盆,就能摆成实心正三角形,如果减少4盆,就能摆成每边多于1个花盆的实心正方形,问将现有的花盆摆成实心矩形,最外层最少有多少盆花?A.22
B.24
C.26
D.28答案:A解析:第一步,本题考查几何构造问题。
第二步,根据题意,增加5盆能摆成实心正三角形,摆成一个边有n个花盆的实心正三角形需要
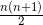
个花盆,则花盆总数为

减少4盆能摆成实心正方形,说明(花盆总数-4)应该是一个平方数。采用特殊值依次代入验证,发现只有当n=9即花盆数为40时,同时满足这两个条件。那么共有40个花盆。
第三步,根据几何最值理论,当四边形面积一定时,越接近正方形,周长越短。故当矩形的两条边分别是5和8时,最外层花盆数最少,此时最外层有(8+5)×2-4=22(盆)花。
因此,选择A选项。
