把10个相同小球放入3个不同箱子，第一个箱子至少1个，第二个箱子至少3个，第三个箱子可以放空球，有几种放法?（ ） A．28种 B．36种 C．56种 D．20种

题目

把10个相同小球放入3个不同箱子，第一个箱子至少1个，第二个箱子至少3个，第三个箱子可以放空球，有几种放法?（ ） A．28种 B．36种 C．56种 D．20种

相似考题

1.三个箱子,第一个箱子中有4个黑球2个白球,第二个箱子中有3个黑球5个白球,第三个箱子中有3个黑球2个白球。试求:随机地取一个箱子,再从这个箱子中任取出一球,这个球为白球的概率是多少?

2.：两个长方体的箱子，箱子A的长、宽、高为：l2、14、16，箱子B的长、宽、高为：15、16、17，则B箱子比A箱子的体积大多少？（ ）A．1286B．1392C．1425D．1532

3.现有三个箱子,第一个箱子放有4本不同的计算机书,第二个箱子放有3本不同的文艺书,第三个箱子放有2本不同的体育书,则从这三个箱子中任取一本书,共有________种不同的取法。A．6B．7C．9D．24

4.把12个球随机地投入三个箱子里,则“第一个箱子里有3个球”这一事件A发生的概率为________。A．0.35B．0.33C．0.25D．0.21

更多“把10个相同小球放入3个不同箱子,第一个箱子至少1个,第二个箱子至少3个,第三个箱子可以放空球,有 ”相关问题

  • 第1题：

    有6个木箱，编号为A，B，C，…，F，每个箱子有一把钥匙，6把钥匙各不相同，每个箱子放进一把钥匙锁好：先打开A、B号箱子，可以取出钥匙去开箱子上的锁，如果最终能把6把锁都打开，则说明这是一种放钥匙的“好”的方法，那么“好”的方法共多少种?（ ）

    A．120

    B．180

    C．216

    D．240


    正确答案：D



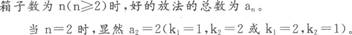
    故本题正确答案为D。

  • 第2题：

    我国的“退耕还林”补贴属于()。

    A、绿箱子补贴

    B、蓝箱子补贴

    C、黄箱子补贴

    D、可诉补贴


    参考答案：A

  • 第3题：

    有6个木箱，编号为1，2，3，4，5，6，每个箱子有一把钥匙，6把钥匙各不相同，每个箱子放进一把钥匙锁好：先打开1,2号箱子，可以取出钥匙去开箱子上的锁，如果最终能把6把锁都打开，则说明这是一种放钥匙的“好”的方法，那么“好”的方法共多少种?（ ）

    A．120

    B．180

    C．216

    D．240


    正确答案：D
    设第1，2，3，…，6号箱子中所放的钥匙号码依次为k1，k2，k3，…，k6。当箱子数为n(n2)时，“好”的放法的总数为an。
    当n＝2时，显然a2＝2(k1＝1，k2＝2或k1＝2，k2＝1)。则此时好方法为2种。
    当n＝3时，显然k3≠3，否则第3个箱子打不开，从而k1＝3或k2＝3，于是n＝2时的每一组解对应n＝3的2组解，即k1＝1，k2＝3，k3＝2；或k1＝3，k2＝2，k3＝1；或k1＝2，k2＝3，k3＝1；或k1＝3，k2＝1，k3＝2。这样就有a3＝2a2—4。则此时好方法为4种。
    当n＝4时，也一定有k4≠4，否则第4个箱子打不开，从而k1＝4或k2＝4或k3＝4，于是n＝3时的每一组解，对应n＝4时的3组解，这样就有a4＝3a3＝12。则此时好方法为2种。
    依次类推，有：
    a6＝5a5＝5×4×3×2×2＝2×5！＝240。故本题正确答案为D。

  • 第4题：

    货轮上卸下若干只箱子，总重量为10吨，每只箱子的重量不超过1吨，为了保证能把这些箱子一次运走，问至少需要多少辆载重3吨的汽车？( )

    A.3
    B.4
    C.5
    D.6

    答案：C
    解析：
    设每辆车实际载重为x，因为每只箱子重量不超过1吨，则每辆车可运走货物不少于2吨.否则可以再放一只箱子上去。因此根据箱子重量不同，有2＜x≤3。若有a辆车，则2a＜ax≤3a，ax为总载重量。无论箱子重量怎样配置，若要一次运走货物，总载重量下限应大于10吨，即2a=10，解得a=5辆。当有4辆车时，若有13只箱子，平均每4只箱子的重量都超过3吨，则不能用4辆车一次运走。因此至少要5辆车才能把这些箱子一次运走。

  • 第5题：

    现有三个箱子，第一个箱子放有4本不同的计算机书，第二个箱子放有3本不同的文艺书，第三个箱子放有2本不同的体育书，则从这三个箱子中任取一本书，共有（ ）种不同的取法。
    A. 6 B. 7 C. 9 D. 24


    答案：C
    解析：
    从这三个箱子中任取一本书，有3类不同的方法：第1类方法是从第一个箱子取1本计算机书，有4种取法；第2类方法是从第二个箱子取1本文艺书，有3种取法；第3类方法是从第三个箱子取1本体育书，有2种取法。根据加法原理可知，不同取法的种数是4+3+2=9（种）。

  • 第6题：

    某种魔方有六面，六面全部复原时的颜色分别为红、蓝、黄、白、绿、橙。在某综艺节目现场，有此种魔方6个，每个只复原了一面，且每个魔方复原面的颜色不同。主持人将此6个魔方放入编号为1—6的6个不透明的箱子中，并打开了1号箱子，里面装的是复原面为蓝色的魔方，随后主持人请刘、赵、唐、郑、杨五位嘉宾猜其他箱子里魔方复原面的颜色。五位嘉宾分别作出了如下猜测：
    刘：3号箱子中魔方复原面为橙色，4号箱子中魔方复原面为黄色。
    赵：3号箱子中魔方复原面为绿色，5号箱子中魔方复原面为红色。
    唐：2号箱子中魔方复原面为红色，6号箱子中魔方复原面为白色。
    郑：4号箱子中魔方复原面为绿色，5号箱子中魔方复原面为白色。
    杨：3号箱子中魔方复原面为黄色，6号箱子中魔方复原面为橙色。
    随后主持人一一打开箱子，发现每位嘉宾都只猜对了一个箱子中魔方复原面的颜色，并且每个箱子都有一位嘉宾猜对。
    由此可以推测：

    A.2号箱子中魔方复原面为绿色
    B.4号箱子中魔方复原面不是黄色
    C.5号箱子中魔方复原面为白色
    D.6号箱子中魔方复原面为红色

    答案：C
    解析：
    第一步，确定题型。
    题干有信息匹配特征，确定为分析推理。
    第二步，分析条件，进行推理。
    根据“每个箱子都有一位嘉宾猜对”，说明每个箱子里的出现的正确颜色都有人提到，根据题干中只有唐的前半句话涉及2号箱子，并且只出现了一次，可以确定此话必为真，因此2号箱子中魔方复原面为红色，那么其他涉及红色的信息都是假的，赵后半句出现5号红色是假的，那么郑说5号是白色是对的。
    因此，选择C选项。

  • 第7题：

    箱子里面有红、白两种玻璃球，红球数比白球数的3倍多两个，每次从箱子里取出7个白球、15个红球。如果经过若干次以后，箱子里只剩下3个白球、53个红球，那么，箱子里原有红球比白球多多少个?

    A.102
    B.104
    C.106
    D.108

    答案：C
    解析：
    设共取了x次，原有红球(53+15x)个，原有白球(3+7x)个，由题意可得，53+15x=3(3+7x)+2，解得x=-7．原有红球比白球多(53+15x)一(3+7x)=106个，应选择C。

  • 第8题：

    有编号从1到5的5个箱子，将10个完全相同的小球放进5个箱子，要求每个箱子里必须有小球且数量不能超过箱子的编号，问符合要求的放小球的方法有多少种？

    A. 21
    B. 22
    C. 23
    D. 24

    答案：B
    解析：
    根据题意每个箱子都要有且数量不能大于编号，现将10个球给每个箱子放一个，还剩余5个球，1号箱子不能再放置。5个球分成4、1，4只能放在5号，1放在2、3、4中的一个，共c3,1=3种；五个球分成3、2，共C2,1×C2,1=4种；五个球分成3、1、1，共C2,1×C3,2=6种；五个球分成2、2、1，共C3,2×C2,1=6种，五个球分成2、1、1、1，共C3,1=3种。总共3+4+6+6+3=22种。答案选B。

  • 第9题：

    货轮上卸下若干只箱子，总重量为10吨，每只箱子的重量不超过1吨，为了保证能把这 些箱子一次运走，问至少需要多少辆载重3吨的汽车？

    A.3
    B.4
    C.5
    D.6

    答案：C
    解析：
    设每辆车实际载重为X，因为每只箱子重量不超过1吨，则每辆车可运走货物不少于2 吨，否则可以再放一只箱子上去。因此根据箱子重量不同，有2 ＜x≤3。若有a辆车，则2a＜xa≤3a，ax为总载重量。无论箱子重量怎样配置，若要一次运走货物，总载重量下限应大于10吨，即2a=10，解得a=5辆。
    当有4辆车时,若有13只箱子，平均每4只箱子的重量都超过3吨，则不能用4辆车一次运走。因此至少要5辆车才能把这些箱子一次运走。

  • 第10题：

    单选题
    把编号为1-5的球放入编号为1-5的箱子，一个箱子只能放一个，要求第1、5号球放入两个编号相邻的箱子的方法有（）种
    A

    24

    B

    32

    C

    48

    D

    60


    正确答案： B
    解析： 1号5号相邻有4种选择，所以4*A（2，2）*A（3*3）=4*2*6=48种。

  • 第11题：

    单选题
    某个装有一层12听可乐的箱子，现在要向箱子中的空隙放入填充物，已知每听可乐直径为6cm，高12cm。则至少要向该箱子放多少填充物？（　　）
    A

    835cm3

    B

    975cm3

    C

    1005cm3

    D

    1115cm3


    正确答案： A
    解析：
    由题意可知，恰好装满这12听可乐的箱子的底面积应为6×6×12＝432cm2，且要使填充物放得最少，则箱子要与可乐同高。至少要向该箱子放入432×12－9π×12×12≈1115cm3的填充物。

  • 第12题：

    152个球，放入若干个同样的箱子中，一个箱子最少放10个，最多放20个，且各个箱子的球数均不相同，问有多少种放法？（不计箱子的排列，即两种放法，经过箱子的重新排列后，是一样的，就算一种放法）

    A. 1

    B. 7

    C. 12

    D. 24


    正确答案：A
    设箱子个数为m，
    因为每只箱子的球数均不相同，最少放10个，最多放20个，所以m≤20-10+1＝11。
    如果m＝11，那么
    球的总数10×11+（0+1+2+…+10）＝110+55＞152，所以m≤10。
    如果m≤9，那么
    球的总数≤10×9+（10+9+8+…+2）＝90+54＝144152，所以m＝10
    在m＝10时，
    10×10+（10+9+…+1）＝155＝152+3，所以一个箱子放10个球，其余箱子分别放11，12，14，15，16，17，18，19，20个球，总数恰好为152，而且符合要求的放法也只有这一种。故本题正确答案为A。

  • 第13题：

    两个长方体的箱子，箱子A的长、宽、高为12、14、16，箱子B的长、宽、高为15、16、17，则B箱子比A箱子的体积大多少？（ ）

    A．1286

    B．1392

    C．1425

    D．1532


    正确答案：B
     根据长方体的体积=长×宽×高，即：A箱子的体积为：12×14×16,B箱子的体积为：15×16×17，相减为：4080-2688=1392，得出答案为1392。

  • 第14题：

    箱子里有红、白两种玻璃球。红球是向球的3倍少2个。每次从箱子里取出7个白球、13个红球，经过若干次后，箱子里剩下6个白球，72个红球，那么，原来箱子里红球比白球多多少个?（ ）

    A．102

    B．104

    C．106

    D．108


    正确答案：D
    假设箱子里原来有白球x个，那么红球为(3x--2)个，依题意有(x－6)÷7=(3x－2－72)÷13，解得x=55，所以原来红球比白球多3×55－2－55=108(个)。故选D。

  • 第15题：

    某个装有一层12听可乐的箱子，现在要向箱子中的空隙放入填充物，已知每听可乐直径为6cm，高12cm。则至少要向该箱子放多少填充物？（ ）

    A. 835cm3
    B. 975cm3
    C. 1005cm3
    D. 1115cm3

    答案：D
    解析：
    恰好装满这12听可乐的箱子的底面积应为6X6X12=432（cm2），且要使填充物放得最少，则箱子要与可乐同高。因此，要向该箱子放入432 X 12－9πX 12 X 12≈ （1115cm3）的填充物。

  • 第16题：

    张三到某店买巧克力，店主领他看四个箱子，每个箱子上都写—句话。第一个箱子：“所有箱子中都有荔枝。”第二个箱子：“本箱中有苹果。”第三个箱子：“本箱中没有巧克力。”第四个箱子：“有些箱子中没有荔枝。”店主对张三说：“四句话中只有一句真话，您看巧克力在哪个箱子里?”请替张三选择一个正确答案。


    A. 巧克力在第一个箱子里
    B. 巧克力在第二个箱子里
    C. 巧克力在第三个箱子里
    D. 巧克力在第四个箱子里

    答案：C
    解析：
    解题指导： 第一个箱子：“所有箱子中都有荔枝。”和第四个箱子：“有些箱子中没有荔枝。”这两个说法矛盾，必定有一真。根据题目条件，另外两个说法都是假的。第三个箱子：“本箱中没有巧克力。”这个说法是假的，因此推定巧克力在第三个箱子里面。寻找矛盾的命题通常可以快速解决这类题目。故答案为C。

  • 第17题：

    如图所示，A、B两个箱子叠放在一起，爸爸和小明分别用大小为F的恒力用力拉，使两个箱子沿水平做匀速直线运动。爸爸个子高，着力点在A箱子上，小明个子矮，着力点在B箱子上。下列说法中，正确的是：


    A.无论是爸爸还是小明拉箱子，箱子A所受的摩擦力大小都为F
    B.无论是爸爸还是小明拉箱子，箱子B受到地面对它的摩擦力均为F
    C.爸爸拉箱子时，箱子A受到的摩擦力为0，箱子B受到地面对它的摩擦力为F
    D.小明拉箱子时，箱子A受到的摩擦力为F，箱子B受到地面对它的摩擦力为

    答案：B
    解析：
    因AB之间没有相对运动，可看做一个整体，由做匀速直线运动可知，箱子受力平衡，故不论爸爸拉箱子还是小明拉箱子，箱子与地面之间的摩擦力大小均为F。当爸爸拉箱子时，F作用在A上，为保持B匀速运动，则AB之间有与地面摩擦力方向相反大小为F的摩擦力作用在B上；当小明拉箱子时B箱受拉力与地面摩擦力二力平衡，故与A之间没有摩擦力。故答案选B。

  • 第18题：

    现有三个箱子,第一个箱子有4个红球,3个白球；第二个箱子有3个红球,3个白球；第三个箱子有3个红球,5个白球；先取一只箱子,再从中取一只球,(1)求取到白球的概率；(2)若取到红球,求红球是从第二个箱子中取出的概率.


    答案：
    解析：

  • 第19题：

    印刷厂印刷了一批共1080本字典，用大、小两种箱子进行分装。已知每个大箱子比小箱子多装15本，且8个小箱子的容量等于3个大箱子的容量。如果只用大箱子进行分装，则至少需要（ ）个大箱子？

    A.40
    B.45
    C.50
    D.55

    答案：B
    解析：
    第一步，本题考查基础应用题，用方程法解题。
    第二步，设小箱子可装x本，则大箱子可装（x＋15）本。由8个小箱子的容量等于3个大箱子列方程：8x＝3（x＋15），解得x＝9，则大箱子可装9＋15＝24（本）。
    第三步，只用大箱子进行分装，则至少需要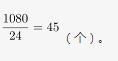

    因此，选择B选项。

  • 第20题：

    现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。

    • A、多1个
    • B、少1个
    • C、多2个
    • D、少2个

    正确答案:A

  • 第21题：

    单选题
    出租车司机张军，将乘客送到公园后，在回来的路上，看到车里有一个纸箱，大约有两个方便面箱子大小。因为不知道里面装的是什么，他赶紧把箱子送到了派出所。民警把箱子拆开一看，里面原来是满满一箱的公园门票。
    A

    乘客捡到了一个纸箱子

    B

    民警将箱子送回了公园

    C

    箱子里有门票和方便面

    D

    司机将箱子送到了派出所


    正确答案： A
    解析： 暂无解析

  • 第22题：

    单选题
    现有3个箱子，依次放入1、2、3个球，然后将3个箱子随机编号为甲、乙、丙，接着在甲、乙、丙3个箱子里分别放入其箱内球数的2、3、4倍，共放了22个球。最终甲箱中的球比乙箱（）。
    A

    多1个

    B

    少1个

    C

    多2个

    D

    少2个


    正确答案： A
    解析： 由题知，甲、乙、丙3个箱子里最终的球数为原球数的3、4、5倍，而原来的球数是1或2或3，设三个箱子原来分别有x、y、z个球，则有x+y+x=6……（1），3x+4y+5x=22……（2），因为比较的是甲和乙的关系，因此我们将z消去，用5×（1）-（2）得2x+y=8.如果x=1，y=6，不符合，如果x=2，y=4，不符合，于是x=3，y=2，选A。

相关内容