1、2、3、4、5、8这七个数字能够组成多少个能被125整除且无重复数字的五位数? A．9 B．12 C．21 D．24

题目

1、2、3、4、5、8这七个数字能够组成多少个能被125整除且无重复数字的五位数? A．9 B．12 C．21 D．24

相似考题

1.用0，1，2，3，4这五个数字可以组成（ ）个大于20000且不能被5整除的、没有重复数字的5位数。A．120B．54C．48D．72

2.由数字1，2，3，4，5组成无重复数字的二位奇数个数是A．5B．8C．10D．12

3.用数0、1、2、3、4能够组成多少个小于1000的没有重复数字的正整数?A．4B．16C．48D．68

4.（9）由1、2、3、4、5 组成没有重复数字且1、2 都不与5 相邻的五位数的个数是（A）36（B）32（C）28（D）24

更多“1、2、3、4、5、8这七个数字能够组成多少个能被125整除且无重复数字的五位数? A.9 B.12 C.21 D.24 ”相关问题

  • 第1题：

    没有重复数字的五位数3a6b5是75的倍数，求这样的五位数有多少个?

    A．1

    B．2

    C．3

    D．4


    正确答案：C
    [答案] C。[解析] 75=25×3，因此3a665能被3和25整除。能被25整除的数，其后两位，也就是b5能被25整除。此时b只能取2或者7。
    若b=2．则3a625要能被3整除，即3+a+6+2+5=16+a能被3整除，a=2、5、8，又由于没有重复数字，因此a=8，只有一个满足条件的数；
    若6=7，同理可得，3+a+6+7+5=21+a能被3整除，a=0、3、6、9，由于没有重复数字，a只能取0或者9两种情况。
    综上，只有38625、30675和39675三个数满足条件。

  • 第2题：

    用数字4、5、6、7、8、9这六个数字组成一个六位数ABCDEF(不一定按给出数字的顺序排列)，若把A移到最后，所得的六位数BCDEFA能被2整除，若再把8移到最后，所得的六位数CDEFAB能被3整除，…，依此类推，若把E移到最后，所得的六位数能被6整除，则六位数ABCDEF的最小值为（ ）。

    A．476598

    B．476589

    C．456789

    D．465879


    正确答案：B
    此题可用排除法，因为把D移到最后，可以被5整除，所以D一定为5，排除C、D；若要保证能被2、4、6整除，所以A、C、E必须是偶数，排除A，故选B。

  • 第3题：

    从数字0、1、2、3、4、5中任意挑选5个组成能被5除尽且各位数字互异的五位数，那么共可以组成多少个不同的五位数?（ ） A．120 B．96 C．20 D．216


    D.只需用考虑这个五位数的个位上是0或5的情况，为0的时候，有5*4*3*2=120中方法；为5的是候，万位上不能为0，则有4*4*3*2=96种，加起来选D。

  • 第4题：

    用数0、1、2、3、4能够组成多少个小于1000的没有重复数字的正整数?

    A． 4

    B．16

    C．48

    D．68


    正确答案：D
    用1个数，有4个正整数；用2个数，有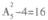个正整数；用3个数，有个正整数，因此总共有4+16+8=68个正整数满足条件。

  • 第5题：

    由1，2，3，4，5这5个数字组成的没有重复数字的五位数中，有多少个大于34152?（）

    A. 50
    B. 54
    C. 58
    D. 60

    答案：C
    解析：
    由题知，满足题意的五位数分为以下几种情况：
    (1)万位数是5的五位数共有4X3X2Xl = 24（个）；
    (2)万位数是4的五位数共有4X3X2X1 = 24（个）；
    (3)万位数是3，则千位数只能是5或4。千位数是5时共有3X2X1 = 6（个）五位数满足题意；千位数是4的满足题意的五位数共有如下4个：34215，34251，34512，34521。
    所以，共有24 + 24 + 6 + 4 = 58 （个）数大于34152。本题正确答案为C。

  • 第6题：

    0、1、2、3、4、5、6这七个数字能够组成多少个被125整除的无重复数字的五位数？

    A.12
    B.21
    C.30
    D.33

    答案：C
    解析：
    能被125整除，则五位数的后三位应该是125、250或者625。
    如果后三位数是125，则有3x3=9个数；
    如果后三位数是250，则有4x3=12个数；
    如果后三位数是625，则有3x3=9个数。
    故一共可以组成9+12+9=30个被125整除且不重复的五位数。

  • 第7题：

    0、1、3、4、7五个数字组成的五位数（数字不允许重复使用）中大于20000的有多少个？

    A.32
    B.36
    C.72
    D.120

    答案：C
    解析：
    本题属于排列组合问题。
    这个数字要大于20000，第一位只能选择3，4，7中的一种，有3种情况，剩余四个数字有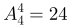种，一共有3×24=72种。
    因此，选择C选项。

  • 第8题：

    用5、6、7、8四个数字组成五位数，数字可重复，组成的五位数中至少有连续三位是5的数字有多少个：
    A 30
    B 33
    C 37
    D 40


    答案：D
    解析：

  • 第9题：

    编程求出个位数字是4且能被7整除的所有3位数之和。


    答案：
    解析：



  • 第10题：

    从0,1,2,3,4,5中任取3个数字,组成能被3整除的无重复数字的3位数有（ ）个

    A.18
    B.24
    C.36
    D.40
    E.96

    答案：D
    解析：

  • 第11题：

    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）

    • A、 “3258能被3整除”是小前提
    • B、 “3258的各位数字之和能被3整除”是大前提
    • C、 “各位数字之和能被3整除的数都能被3整除” 是省略的大前提
    • D、 “3258能被3整除”是大前提

    正确答案:C

  • 第12题：

    单选题
    用数字1，2，3，4，5组成没有重复数字的五位数，其中小于50000的数共有（　　）个．
    A

    36

    B

    72

    C

    84

    D

    96


    正确答案： D
    解析：
    令该五位数的最高位小于5即为1、2、3、4即可，则从最高位到最低位分别共有4、4、3、2、1种选择，共有4×4×3×2×1＝96个．

  • 第13题：

    从2，3，4，5，6这五个数字中挑选两个，组成一个两位数，使其不能被3整除，则有多少种取法?


    正确答案：14

  • 第14题：

    0、1、2、3、4、5、8这七个数字能够组成多少个能被125整除且无重复数字的五位数?

    A．9

    B．12

    C．21

    D．24


    正确答案：C
    能被125整除，则符合题意的五位数的后三位应该是125或者250。如果后三位数是125，则有3×3=9个数；如果后三位数是250，则有4×3=12个数。故一共可以组成9+12=21个能被125整除的五位数。

  • 第15题：

    用数字1，2，3，4，5组成的无重复数字的四位偶数的个数为

    A．8 B．24 C．48 D．120


    正确答案：C

  • 第16题：

    1、2、3、4、5、6这七个数字能够组成多少个被125整除的无重复数字的五位数? A．9 B．12 C．21 D．24


    正确答案：C
    能被125整除，则五位数的后三位应该是125或者250。如果后三位数是125，则有3×3=9个数；如果后三位数是250，则有4×3=12个数。
    故一共可以组成9+12=21个被125整除的五位数。

  • 第17题：

    从1、2、3、4、5、6、7、8、9这几个数字中选择3个数字，使它们的乘积能够被9整除，问共有多少种不同的方法？( )

    A.34
    B.36
    C.27
    D.25

    答案：A
    解析：
    9=1×9=3×3。1～9中的三个自然数的乘积能被9整除，可以分为两种情况：(1)这三个数字中有9，则另外两个数字可在剩下8个数中任意选择，有C28=28种；(2)这三个数字中没有9，则这三个数字中必有3和6.第三个数字有9-3=6种选择。由加法原理可知，共有28+6=34种选择。

  • 第18题：

    1、2、3、4、5、6、7、8、9这九个数字各用一次，组成三个能被9整除的三位数，这三个数的和最大是：

    A.2007
    B.2394
    C.2448
    D.2556

    答案：C
    解析：
    第一步，本题考查多位数问题。
    第二步，1—9这九个数字各用一次，先将1—9加和为45，组成三个能被9整除的三位数，可知每个三位数各位数字加和均为9的倍数，则三个三位数各位数字加和分别为9、18、18。
    第三步，要使这三个数的和最大，则每个三位数百位上的数字应尽量大，先考虑和为9的三位数，百位最大为6，这个三位数是621，剩余两个三位数最大分别为954和873，则954＋873＋621＝2448（可用尾数法，尾数为8）。

  • 第19题：

    由数字1、2、3、4、5、6可组成多少个没有重复数字的四位奇数?( )

    A.15
    B.180
    C.720
    D.4096

    答案：B
    解析：
    根据题意可知，个位数必须用奇数，有3种选择，则总共有3XA53=3×5×4x3=180个。故选B。

  • 第20题：

    从0，2，4，6中取出3个数字，从1，3，5，7中取出两个数字，共能组成多少个没有重复数字且大于65000的五位数


    答案：
    解析：
    根据约束条件“大于65000的五位数”可知这样的五位数只有 7××××、65×××、67×××三种类型．
    (1)能组成7××××型的五位数的个数是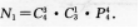

    (2)能组成65×××型的五位数的个数是

    (3)能组成67×××型的五位数的个数是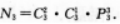

    故所求的五位数的个数为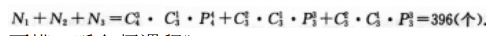

  • 第21题：

    由1,2,3,4,5构成的无重复数字的五位数中,大于34000的五位数有（ ）个

    A.36
    B.48
    C.60
    D.72
    E.90

    答案：C
    解析：

  • 第22题：

    从1、2、3、4、5、6、7、8、9这几个数字中选择3个数字，使它们的乘积能够被9整除，问共 有多少种不同的方法？

    a.34 b.36 c.27 d.25


    答案：A
    解析：
    9=lx9=3x3。1~9中的三个自然数的乘积能被9整除，可以分为两种情况：（1)这三个数 字中有9，则另外两个数字可在剩下8个数中任意选择，有C82=28种；（2)这三个数字中没有9,则这三个数字中 必有3和6,第三个数字有9-3=6种选择。由加法原理可知，共有28+6=34种选择。

  • 第23题：

    单选题
    三段论：“因为3258的各位数字之和能被3整除，所以3258能被3整除”。前提是（）
    A

     “3258能被3整除”是小前提

    B

     “3258的各位数字之和能被3整除”是大前提

    C

     “各位数字之和能被3整除的数都能被3整除” 是省略的大前提

    D

     “3258能被3整除”是大前提


    正确答案： C
    解析： 暂无解析

相关内容