已知文法G1＝(VT＝{a,b,d}，VN＝{S，A，B}，S,P)，其中P为： S→dAB A→aA|a B→bB|ε 该文法属于(28)文法。A．0型B．上下文有关C．上下文无关D．正规
题目
已知文法G1＝(VT＝{a,b,d}，VN＝{S，A，B}，S,P)，其中P为： S→dAB A→aA|a B→bB|ε 该文法属于(28)文法。
A．0型
B．上下文有关
C．上下文无关
D．正规
相似考题
更多“已知文法G1=(VT={a,b,d},VN={S,A,B},S,P),其中P为: S→dAB A→aA|a B→bB|ε 该文法属于 ”相关问题
-
第1题：
已知文法G2=(VT={a，'，'，(,)}，VN={S，L)，S,P)，其中P为 S→(L)|a L→-L，s|s 与G2等价的不含左递归规则的文法是(29)。
A．G21=(VT={a，'，'，(,)}，VN={S，L}，S，P)，其中P为 S→(L)|a L→S，S|S
B．G22=(VT＜a，'，'，(,)}，VN={S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' L'→SL'|ε
C．G23=(VT{a，'，'，(,)}，VN={S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' U→,SL'|ε
D．G24=(VT=(a，'，'，(,)}，VN=＜S，L，L'}，S，P)，其中P为 S→(L)|a L→SL' L→SL'|S
正确答案：C
解析：采用自顶向下的预测分析法首先是等价改写给定的文法，消除文法的左递归和提取产生式的公共左因子。消除直接左递归的方法如下：若A→Aα|β，其中α，β∈(VT∪VN)*，β不以A开始，则关于A的这种形式的产生式可改写成A→βA'A'→αA'|ε一般而言，假设A的产生式为A→Aα1|Aα2|…|Aαn|β1|β2|…|βm其中αI(i=1，2，…，n)不等于ε，βj(j=1，2，…，m)不以A开始，那么上述产生式可改成A→β1A'|β2A'|…|βmA'A'→α1A'|α2A'|…|αnA'|ε消除文法G2中规则的左递归后，其规则变成S→(L)|aL→SL'L'→，SL'|ε -
第2题：
已知文法G2=(VT={a，'，'，(,)}，VN{S,L}，S，P)，其中P为， S→(L)|a L→L，S|S (a，(a，a))是L(G2[S])的句子，这个句子的最左推导是(28)
A．
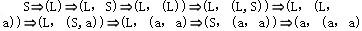
B．
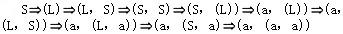
C．
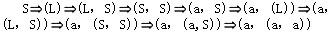
D．
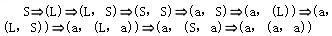正确答案：C
解析：设文法G=(VT，VN，S，P)，A→β∈P，γ，δ∈V*，则称γAδ直接推导出γβδ，表示成：γAδγβδ也称γβδ直接归约到γAδ。对于以上公式，若γ∈VT*，即A是γAδ中最左边的非终结符号，则称以上公式是一个最左推导。若Sa的每一步都是最左推导，则称Sa是一个最左推导，a称为一个左句型。对于以上公式，若δ∈VT*，即A是γAδ中最右边的非终结符号，则称以上公式是一个最右推导。若Sa的每一步都是最右推导，则称Sa是一个最右推导，a称为一个右句型。最右推导也称作规范推导，右句型也称作规范句型。对于句子(a，(a，a))，被选择答案中A是最右推导，C是最左推导，B和D的推导序列中，既有最左推导，又有最右推导。 -
第3题：
已知文法G1=(VT={a,b,d}，VN={S，A，B}，S,P)，其中P为， S→dAB A→aA|a B→bB|ε 该文法生成的语言是(28)。
A．{dambn|m≥0，n≥O}
B．{dambn|m≥1，n≥0}
C．{dambn|m≥0，n≥1}
D．{dambn|m≥1，n≥1}
正确答案：B
解析：已知文法G=(VT，VN，S，P)，它所产生的语言定义如下：若有S(11)w，则称w是文法G的一个句型。仅含终结符的句型是一个句子。语言L(G)是由文法G产生的所有句子组成的集合：L(G)={w|Sw且w∈VT*}推导的定义如下：设文法G=(VT，VN，S，P)，A→β∈P，γ，δ∈V*，则稀γAδ直接推导出γβδ，表示成这个定义告诉我们，若知道γAδ∈V*，根据A→β∈，可求出γβδ∈V*，方法是用A→β的右部β替换γAδ中的A得到γβδ；相反，若知道γβδ∈V*，根据A→β∈P，可求出γAδ∈V*，方法是用A→p的左部A替换γβδ中的β得到γAδ。若存在一个推导序列：，则称从a0经n步推导出an，表示成根据文法G1的第1条规则S→dAB知道，文法G1产生的句子的第1个字符是d，后跟着由A产生的终结字符串，再后边跟着由B产生的终结字符串。根据文法G1的第2条规则A→aA|a知道，由A产生的终结字符串是{am|m1}；根据B的规则B→bB|ε知道，由B产生的终结字符串是{bn|0}。因此，L(G1)={dambn|m1，n0}。 -
第4题：
设语言L={w|w∈{a,b}+且w中a和b的个数相等}，产生语言L的上下文无关文法是(28)。
A．Ga=(VT={a,b}，VN={S，A，B}，S,P)，其中P为， S→a|aA|bSS A→aB|bS B→b|bA|aBB
B．Gb=(VT={a,b}，VN={S,A,B}，S,P)，其中P为， S→b|bB|aSS B→aS|bA A→a|aB|bAA
C．Gc=(VT={a,b}，VN{S,A,B}，S,P)，其中P为， S→aB|bA A→a|aS|bAA B→b|bS|aBB
D．Gd=(VT={a,b}，VN={S，A，B}，S,P)，其中P为， S→aB|bA|s A→aS|bAA B→bS|aBB
正确答案：C
解析：字母表{a,b}上的任何非空串，从其所含a和b的个数来划分，分成下面3个集合：①a和b的个数相等：②a比b的个数多，但仅要a比b的个数多1个的那些子串；③b比a的个数多，但仅要b比a的个数多1个的那些子串。通过上面的分析，根据用文法规则产生句子的原理，设3个非终结符号，不妨称做S、A、B，它们的产生式分别完成：①用S的产生式推导出a和b的个数相等的串；②用A的产生式推导出a比b的个数多1个的串；③用B的产生式推导出b比a的个数多1个的串。根据3个非终结符号S、A、B的含义，显然，关于S的产生式应该是S→aB|bA。对于A产生的串，若第1个字符是a，则剩下的是a和b的个数相等的串：若第1个字符是b，则跟随b的是a比b的个数多2个的串，这个串是两个a比b的个数多1个的子串。根据上述分析，写出关于A的产生式A→a|aS|bAA。可以通过和A类似的分析，写出关于B的产生式B→b|bS|aBB。可以用归纳法证明上面所写的文法是正确的。现在，我们很清楚被选答案中的4个文法所描述的语言，它们分别是：L(Ga)={w|w∈{a,b}+且w中a比b的个数多一个}L(Gb)={w|w∈{a,b}+且w中b比a的个数多一个}L(Gc)={w|w∈{a,b}+且w中a和b的个数相等}L(Gd)={w|w∈{a,b}+且w中a和b的个数相等} -
第5题：
己知文法G2=(VT＝{a，'，'，(，)}，VN={S，L}，S，P)，其中P为， S→(L)|a L→L，S|S 右句型(L，(L，S))的句柄是(28)。
A．(L，(L，S))
B．(L，S)
C．L,S
D．S
正确答案：C
解析：在自底向上分析的过程中，按最右推导的逆过程构造出最右推导，称为规范归约。关键是每步找出被归约的右句型的“可归约串”，称为“句柄”。请读者仔细领会句柄的定义。右句型(最右推导推导出的句型)γ的句柄是一个产生式A→β以及γ中的一个位置，根据这个位置可找到β，用A代替β得到最右推导的前一个右句型。即如果有下面的最右推导：SaAwaβw那么，在a后A→β是aβw的句柄。句柄右边的w仅含终结符号。有的教课书上，句柄的定义借助于短语、直接短语的定义给出：设G＝(VT,VN，S，P)足一个文法，若SaAγaβγ则在句型aβγ中，β是相对于非终结符号A的短语。又若SaAγaβγ则在句型αβγ中，β是相对于非终结符号A的直接短语，最左边的直接短语称为句柄。根据句型(L，(L,S))的最右推导：S(L,(L))(L，(L，S))(此步最右推导使用规则S→L，S)因此，(L，(L,S)中的L,S是句型(L，(L,S))的句柄。