【C程序】#include<stdio.h>／*此处为栈类型及其基本操作的定义，省略*／int main()｛STACK station;int state[1000];int n; ／*车厢数*／int begin, i, j, maxNo; ／*maxNo为A端正待入栈的车厢编号*／printf("请输入车厢数：");scanf("%d",&n);printf(“请输入需要判断的车厢编号序列（以空格分隔）：”);if（n＜1）return-1;for (i＝0; i<n; i++) ／*读入需要驶出的

阅读下列说明和C代码，将应填入(n)处的字句写在对应栏内。

【说明】

栈(Stack)结构是计算机语言实现中的一种重要数据结构。对于任意栈，进行插入和删除操作的一端称为栈顶(Stock Top)，而另一端称为栈底(Stock Bottom)。栈的基本操作包括：创建栈(NewStack)、判断栈是否为空(IsEmpty)、判断栈是否已满(IsFull)、获取栈顶数据(Top)、压栈/入栈(Push)、弹栈/出栈(Pop)。

当设计栈的存储结构时，可以采取多种方式。其中，采用链式存储结构实现的栈中各数据项不必连续存储(如下图所示)。

以下C代码采用链式存储结构实现一个整数栈操作。

【C代码】

typedef struct List {

int data； //栈数据

struct List* next； //上次入栈的数据地址

}List；

typedef struct Stack{

List* pTop； //当前栈顶指针

}Stack；

Stack* NewStack() {return (Stack*) calloc(1/sizeof(Stack))；}

int IsEmpty(Stack* S){//判断栈S是否为空栈

if((1))return 1;

return 0;

}

int Top(Stack* s){//获取栈顶数据。若栈为空，则返回机器可表示的最小整数

if(IsEmpty(S))return INT_ MIN；

return (2)；

}

void Push(Stack* S，int theData) {//将数据theData压栈

List* newNode；

newNode=(List*)calloc(1/sizeof (List))；

newNode-＞data=theData；

newNode-＞next=S-＞pTop；

S-＞pTop=(3)；

}

void Pop(Stack* S) {//弹栈

List* lastTop；

if(IsEmpty(S) ) return；

lastTop=S-＞pTop；

S-＞pTop=(4)；

free(lastTop)；

}

define MD(a) a＜＜2

int main(){

int i;

Stack* myStack；

myStack= NewStack()；

Push(myStack，MD(1))；

Push(myStack，MD(2))；

Pop(myStack)；

Push(myStack，MD(3)+1)；

while( !IsEmpty(myStack) ){

printf("%d"，Top(myStack))；

Pop(myStack)；

}

return 0；

}

以上程序运行时的输出结果为:(5)

（12）假定栈用顺序的方式存储，栈类型 stack定义如下：

TYPE stack=RECORD

A：ARRAY［l..m0] OF datatype;

t：O..m0;

END；

下面是栈的一种基本运算的实现：

PROCEDURE xxxx(VAR s:satack)；

BEGIN

IF s.t＝0

THEN print（‘underflow’）

ELSE s.t：＝s.t-1；

END;

请问这是栈的哪一种基本运算？

A) 栈的推入

B)栈的弹出

C）读栈顶元素

D)将栈置为空栈

试题七（共 15 分）

阅读以下说明和C程序，将应填入 （n） 处的字句写在答题纸的对应栏内。

【说明】

现有 n（n < 1000）节火车车厢，顺序编号为 1,2,3,...,n，按编号连续依次从 A方向的铁轨驶入，从 B 方向铁轨驶出，一旦车厢进入车站（Station）就不能再回到 A方向的铁轨上；一旦车厢驶入 B 方向铁轨就不能再回到车站，如图 7-1所示，其中 Station 为栈结构，初始为空且最多能停放 1000 节车厢。

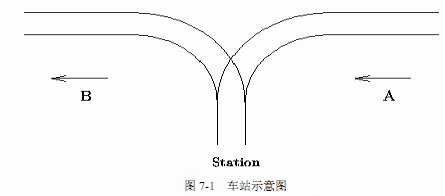
下面的 C 程序判断能否从 B 方向驶出预先指定的车厢序列，程序中使用了栈类

STACK,关于栈基本操作的函数原型说明如下：

void InitStack(STACK *s)：初始化栈。

void Push(STACK *s,int e): 将一个整数压栈，栈中元素数目增 1。

void Pop(STACK *s)：栈顶元素出栈，栈中元素数目减 1。

int Top(STACK s)：返回非空栈的栈顶元素值，栈中元素数目不变。

int IsEmpty(STACK s)：若是空栈则返回 1，否则返回 0。

【C 程序】

include<stdio.h>

/*此处为栈类型及其基本操作的定义，省略*/

int main( ){

STACK station;

int state[1000];

int n; /*车厢数*/

int begin, i, j, maxNo; /*maxNo 为 A端正待入栈的车厢编号*/

printf("请输入车厢数： ");

scanf("%d",&n);

printf("请输入需要判断的车厢编号序列（以空格分隔） ： ");

if (n < 1) return -1;

for (i = 0; i<n; i++) /* 读入需要驶出的车厢编号序列,存入数组 state[] */

scanf("%d",&state[i]);

（1） ; /*初始化栈*/

maxNo = 1;

for(i = 0; i < n; ){/*检查输出序列中的每个车厢号 state[i]是否能从栈中获取*/

if ( （2） ){/*当栈不为空时*/

if (state[i] == Top(station)){ /*栈顶车厢号等于被检查车厢号*/

printf("%d ",Top(station));

Pop(&station); i++;

}

else

if ( （3） ){

printf("error\n");

return 1;

}

else {

begin = （4） ;

for(j = begin+1; j<=state[i]; j++) {

Push(&station, j);

}

}

}

else { /*当栈为空时*/

begin = maxNo;

for(j = begin; j<=state[i]; j++){

Push(&station, j);

}

maxNo = （5） ;

}

}

printf("OK");

return 0;

}