考虑表6—1的实例,假设有3个物品,背包容量为22。图6—6中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字I/O分别表示选择/不选择对应物品。除了根结点之外,每个左孩子结点旁边的上下两个数字分别表示当前背包的重量和已获得的价值,右孩子结点旁边的数字表示扩展了该结点后最多可能获得的价值。为获得最优解,应该选择物品 (5) ,获得的价值为 (6)。对于表6—1的实例,若采用穷举法搜索整个解空间,则搜索树的结点数为 (7) ,而用了上述回溯法,搜索树的结点数为 (8) .
题目
考虑表6—1的实例,假设有3个物品,背包容量为22。图6—6中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字I/O分别表示选择/不选择对应物品。除了根结点之外,每个左孩子结点旁边的上下两个数字分别表示当前背包的重量和已获得的价值,右孩子结点旁边的数字表示扩展了该结点后最多可能获得的价值。为获得最优解,应该选择物品 (5) ,获得的价值为 (6)。
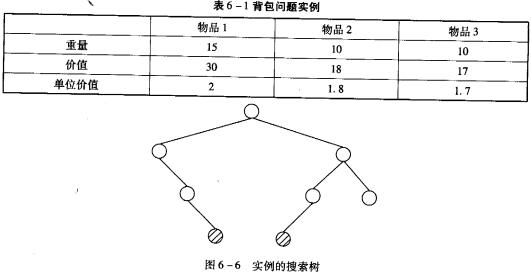
对于表6—1的实例,若采用穷举法搜索整个解空间,则搜索树的结点数为 (7) ,而用了上述回溯法,搜索树的结点数为 (8) .
相似考题
更多“ 考虑表6—1的实例,假设有3个物品,背包容量为22。图6—6中是根据上述算法构造的搜索树,其中结点的编号表示了搜索树生成的顺序,边上的数字I/O分别表示选择/不选择对应物品。除了根结点之外,每个左孩子结点旁边的上”相关问题
-
第1题:
【问题 1】(8 分)
用回溯法求解此 0-1 背包问题,请填充下面伪代码中(1)~(4)处空缺。
回溯法是一种系统的搜索方法。在确定解空间后,回溯法从根结点开始,按照深度优先策略遍历解空间树,搜索满足约束条件的解。对每一个当前结点,若扩展该结点已经不满足约束条件,则不再继续扩展。为了进一步提高算法的搜索效率,往往需要设计一个限界函数,判断并剪枝那些即使扩展了也不能得到最优解的结点。现在假设已经设计了BOUND( v,w,k,W )函数,其中 v、w、k 和 W分别表示当前已经获得的价值、当前背包的重量、已经确定是否选择的物品数和背包的总容量。对应于搜索树中的某个结点,该函数值表示确定了部分物品是否选择之后,对剩下的物品在满足约束条件的前提下进行选择可能获得的最大价值,若该价值小于等于当前已经得到的最优解,则该结点无需再扩展。
下面给出 0-1背包问题的回溯算法伪代码。
函数参数说明如下:
W:背包容量;n:物品个数;w:重量数组;v:价值数组;fw:获得最大价值时背包的重量;fp:背包获得的最大价值;X:问题的最优解。
变量说明如下:
cw:当前的背包重量;cp:当前获得的价值;k:当前考虑的物品编号;Y:当前已获得的部分解。
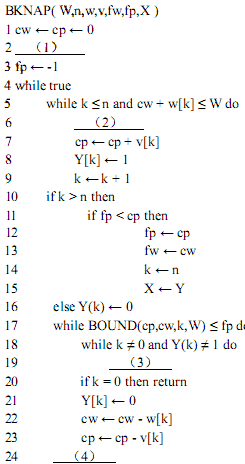 正确答案:
正确答案:
(1)k←1或其等价形式(2)cw←cw+w[k]或其等价形式(3)k←k–1或其等价形式(4)k←k+l或其等价形式 -
第2题:
一棵二叉树顺序编号为6的结点(树中各结点的编号与等深度的完全二叉树中对应位置上结点的编号相同),若它存在右孩子,则右孩子的编号为()。
13
略 -
第3题:
0-1背包问题的回溯算法,下面的解释不正确的是
A.解空间树是子集树#B.左(1)分支的剪枝:选择装入背包的物品重量之和超出背包容量就剪枝#C.右(0)分支的剪枝:已装入背包内的物品价值和+剩余物品装剩余背包容量所能获得的最大价值(物品可分割,也就是用背包问题的贪心算法求得的最大价值)>当前最优值bestp, 就剪枝.#D.当搜索至叶子结点时,一定是发现了到目前为止最好的解使用约束函数剪去不合理的左子树(装该物品)。;使用限界函数剪去得不到更优解的右子树(不装该物品)。 -
第4题:
对二叉树中的结点如下编号:树根结点编号为1,根的左孩子结点编号为2、右孩子结点编号为3,依此类推,对于编号为i的结点,其左孩子编号为2i、右孩子编号为2i+1。例如,下图所示二叉树中有6个结点,结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么,当结点数为n(n>0)的( )时,其最后一个结点编号为2i-1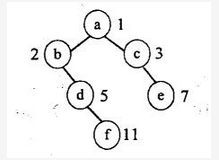 A.二叉树为满二叉树(即每层的结点数达到最大值)
A.二叉树为满二叉树(即每层的结点数达到最大值)
B.二叉树中每个内部结点都有两个孩子
C.二叉树中每个内部结点都只有左孩子
D.二叉树中每个内部结点都只有右孩子答案:C解析:本题考察二叉树的基础知识。可采用验证法。结点数为1时,只有一个结点,编号为1。结点数为2时,最后一个结点为3,那也说明只有左孩子。结点数为3时,最后一个结点编号为7。 -
第5题:
一棵二叉树顺序编号为6的结点(树中各结点的编号与等深度的完全二叉中对应位置上结点的编号相同),若它存在右孩子,则右孩子的编号为()。
13
略
