采用McCabe度量法计算下图的环路复杂性为(29)。 A.2 B.3 SXB采用McCabe度量法计算下图的环路复杂性为（29）。A.2B.3C.4D.5

题目
采用McCabe度量法计算下图的环路复杂性为(29)。 A.2 B.3 SXB

采用McCabe度量法计算下图的环路复杂性为（29）。

A.2

B.3

C.4

D.5

相似考题

1.采用McCabe度量法计算下图的环路复杂性为（31） 。A.2B.3C.4D.5

2.下图所示的程序流程图中有 (34)条不同的简单路径。采用McCabe度量法计算该程序图的环路复杂性为 (35) 。A.3B.4C.5D.6

3.下图所示的程序流程图中有 （请作答此空） 条不同的简单路径，采用McCabe度量法计算该程序图的环路复杂性为 （） 。 A.3 B.4 C.5 D.6

4.采用McCabe度量法计算下图所示程序的环路复杂性为()。A.1B.2C.3D.4

参考答案和解析
正确答案：C
??本题考查环路复杂性的计算，是考试中常考的一个知识点。对于这类试题，我们可以采用结点数-边的条数+2这个公式来计算。在本题给出的图中，结点个数为6，而边的条数为8条（注意最上面的表和语句2过去的边是重合的，因此可视为同一条边），因此环路复杂性为4。也可以根据划分的区域数来计算，图中的边将整个图的平面分割成4个区域，因此结果也为4。??
更多“采用McCabe度量法计算下图的环路复杂性为(29)。 A.2 B.3 SXB ”相关问题

  • 第1题：

    采用McCabe度量法计算下列程序图的环路复杂性为（ ）

    A.2
    B.3
    C.4
    D.5

    答案：C
    解析：
    在一个强连通的有向图G中，环的个数为m-n+2p。其中m为图中弧的个数，n为图中的结点数，p是图中强连通分量的个数。题图为一强连通图，故p=1，而图中弧的个数为8，结点数为6，故环的个数为8-6+2=4。

  • 第2题：

    下图所示的程序流程图中有（34）条不同的简单路径，采用McCabe度量法计算该程序图的环路复杂性为（35）。

    A.3
    B.4
    C.5
    D.6

    答案：A
    解析：
    三条简单路径分别为begin-＞y=n-1成立-＞output A-＞end；begin-＞y=n-1不成立-＞A[i]＞A[i+1]不成立-＞y=n-1成立->end；begin-＞y-n-1不成立-＞A[i]＞A[i+1]成立-＞swapA[I]，A[i+1]-＞y=n-1成立-＞end；MacCabe度量法公式为V（G）=m-n+2，V（G）是有向图G中环路数，m是图G中弧数，n是图G中结点数。本题中m=10，n=9，故V（G）=3。

  • 第3题：

    采用McCabe度量法计算该程序的环路复杂性为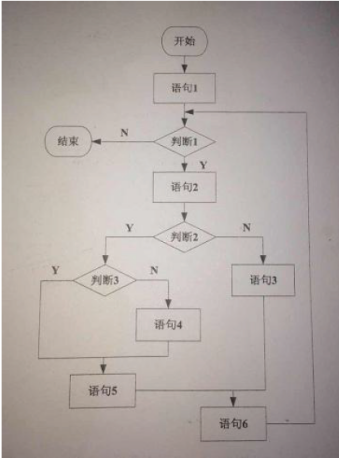

    A.1
    B.2
    C.3
    D.4

    答案：D
    解析：
    将图中的语句与判断条件都抽象为节点，箭线抽象为边，则根据公式V（G）=m-n+2=13-11+2=4

  • 第4题：

    采用McCabe度量法计算下列程序图的环路复杂性为（32）。

    A.2
    B.3
    C.4
    D.5

    答案：C
    解析：
    在一个强连通的有向图G中，环的个数为m-n+2p。其中m为图中弧的个数，n为图中的结点数，p是图中强连通分量的个数。题图为一强连通图，故p=1，而图中弧的个数为8，结点数为6，故环的个数为8-6+2=4。

  • 第5题：

    对下图所示流程图采用McCabe度量法计算该程序的环路复杂性为（ ）

    A.1
    B.2
    C.3
    D.4

    答案：D
    解析：
    环形复杂度V(G)=E-N+2，其中，E是流图中边的条数，N是结点数。
    V(G)=E-N+2=10-8+2=4。

相关内容