图2-36是带权的有向图G的邻接表。以结点V1出发深度遍历图G所得的结点序列为(1);广度遍历图G所得的结点序列为(2);G的一种拓扑序列是(3);从结点V1到V8结点的最短路径是(4);从结点V1到V8结点的关键路径是(5)。A.V1,V2,V3,V4,V5,V6,V7,V8B.V1,V2,V3,V8,V4,V5,V6,V7C.V1,V2,V3,V8,V4,V5,V7,V6D.V1,V2,V3,V8,V5,V7,V4,V6
题目
图2-36是带权的有向图G的邻接表。以结点V1出发深度遍历图G所得的结点序列为(1);广度遍历图G所得的结点序列为(2);G的一种拓扑序列是(3);从结点V1到V8结点的最短路径是(4);从结点V1到V8结点的关键路径是(5)。
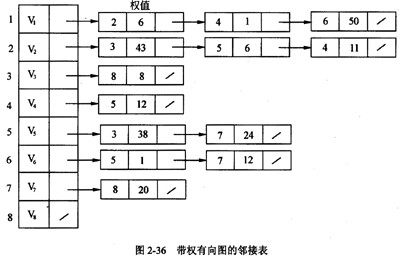
A.V1,V2,V3,V4,V5,V6,V7,V8
B.V1,V2,V3,V8,V4,V5,V6,V7
C.V1,V2,V3,V8,V4,V5,V7,V6
D.V1,V2,V3,V8,V5,V7,V4,V6
相似考题
更多“ 图2-36是带权的有向图G的邻接表。以结点V1出发深度遍历图G所得的结点序列为(1);广度遍历图G所得的结点序列为(2);G的一种拓扑序列是(3);从结点V1到V8结点的最短路径是(4);从结点V1到V8结点的关”相关问题
-
第1题:
某二叉树的先序遍历(根、左、右)序列为 EFHIGJK 、中序遍历(左、根、右)序列为 HFIEJKG, 则该二叉树根结点的左孩子结点和右孩子结点分别是(37)A.A,I.K
B. F,I
C. F,G
D.I,G答案:C解析:由先序遍历看,E为根节点,F为根节点的作孩子。在看中序遍历,则左树有:IE两个子结点。那么E的右孩子结点为G。 -
第2题:
图G的邻接矩阵如下图所示(顶点依次表示为v0、v1、v2、v3、v4、v5),G是(请作答此空)。对G进行广度优先遍历(从v0开始),可能的遍历序列为( )。
 A.无向图
A.无向图
B.有向图
C.完全图
D.强连通图答案:B解析: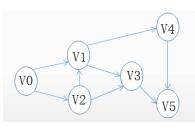
-
第3题:
无向连通图 G 是欧拉图,当且仅当
A.G 不含奇数度结点
B.G含有奇数度结点
C.G 的所有结点度数为偶数
D.G既含有奇数度结点,又含有偶数度结点
G 不含奇数度结点;G 的所有结点度数为偶数 -
第4题:
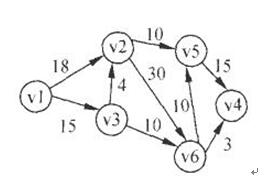
针对下图所示的有向图,从结点V1出发广度遍历所得结点序列和深度遍历所得结点序列分别是______。
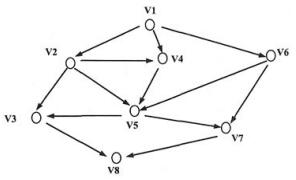 A.V1,V2,V3,V4,V5,V6,V7,V8和V1,V2,V3,V8,V5,V7,V4,V6
A.V1,V2,V3,V4,V5,V6,V7,V8和V1,V2,V3,V8,V5,V7,V4,V6
B.V1,V2,V4,V6,V3,V5,V7,V8和V1,V2,V3,V8,V5,V7,V4,V6
C.V1,V2,V4,V6,V3,V5,V7,V8和V1,V2,V3,V8,V4,V5,V6,V7
D.V1,V2,V4,V6,V7,V3,V5,V8和V1,V2,V3,V8,V5,V7,V4,V6答案:B解析:本题考查遍历方面的基础知识。图的广度优先遍历是先访问顶点V1,然后访问V1邻接到的所有未被访问过的顶点V2,V3,…,Vt邻接到的所有未被访问的顶点。如此进行下去,直到访问遍所有顶点,因此,本题中图的广度优先遍历是V1,V2,V4,V6,V3,V5,V7,V8。深度优先遍历是从图中某个结点,例如V1出发,访问此结点,然后依次从V1的未被访问的邻接顶点出发进行深度优先遍历,直至图中所有和V1有路径想通的结点都被访问到。若此时图中尚有顶点未被访问,则另选图中一个未被访问过的顶点作起始顶点,重复上述过程,直至图中所有顶点都被访问到为止。因此,本题中图的深度优先遍历是V1,V2,V3,V8,V5,V7,V4,V6。 -
第5题:
已知某带权图G的邻接表如下所示,其中表结点的结构为:
则图G是( )。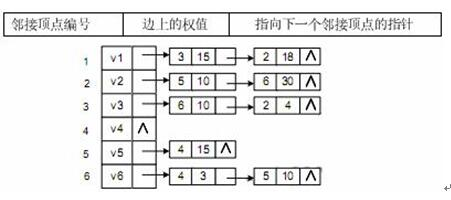 A.无向图
A.无向图
B.完全图
C.有向图
D.强连通图答案:C解析:本题考查数据结构基础知识。
从题中的邻接表中可知,该图的边为、 、 、 、 、 、 、 、 ,如下图所示,显然,这是个有向图。
在无向图中,若存在边(vi,vj),则它同时为vj和vi之间的边。在上面的邻接表中,存在边,而不存在 ,因此该图不是无向图。
对于无向图,其边数e和顶点数n的关系为e=n×(n-1)/2。对于有向图,其边数e和顶点数n的关系为e = n×(n-1),因此该图不是完全图。
若有向图为强连通图,则任意两个顶点间要存在路径。在该有向图中,由于顶点v4没有出边,因此,不存在v4到其他顶点的路径,因此该图不是强连通图。
