对于求取两个长度为n的字符串的最长公共子序列(LCS)问题,利用(24)策略可以有效地避免子串最长公共子序列的重复计算,得到时间复杂度为O(n2)的正确算法。串 <1,0,0,1,O,1,0,1>和<0,1,0,1,1,0,1,1>的最长公共子序列的长度为(25)。A.分治B.贪心C.动态规划D.分支—限界
题目
对于求取两个长度为n的字符串的最长公共子序列(LCS)问题,利用(24)策略可以有效地避免子串最长公共子序列的重复计算,得到时间复杂度为O(n2)的正确算法。串 <1,0,0,1,O,1,0,1>和<0,1,0,1,1,0,1,1>的最长公共子序列的长度为(25)。
A.分治
B.贪心
C.动态规划
D.分支—限界
相似考题
更多“对于求取两个长度为n的字符串的最长公共子序列(LCS)问题,利用(24)策略可以有效地避免子串最长公 ”相关问题
-
第1题:
求解两个长度为n的序列X和Y的一个最长公共子序列(如序列ABCBDAB和BDCABA的一个最长公共子序列为BCBA)可以采用多种计算方法。如可以采用蛮力法,对X的每一个子序列,判断其是否也是Y的子序列,最后求出最长的即可,该方法的时间复杂度为(请作答此空)。经分析发现该问题具有最优子结构,可以定义序列长度分别为i和j的两个序列X和Y的最长公共子序列的长度为c[i,j],如下式所示。

采用自底向上的方法实现该算法,则时间复杂度为( )A.O(n^2)
B.O(n^21gn)
C.O(n^3)
D.O(n2^n)答案:D解析:蛮力法,对X的每一个子序列,判断是否也是Y的子序列,其中,长度为n的序列X共有2^n个子序列,判断其是否是Y的子序列时间是n,因此是n*2^n;采用动态规划法自底向上实现时,根据递归公式,实际是关于i和j的两重循环,因此时间复杂度是n^2. -
第2题:
1、给定两个序列分别为“algorithm”和“glorhythm”。则以下分别为两序列的最长公共子序列和最长公共子串的选项是____
A.gorthm thm
B.thm gorthm
C.glorhthm orthm
D.orthm glorhthm
gorthm thm -
第3题:
如果仅需要求得最长公共子序列的代价,则最长公共子序列的空间复杂性可以降低到O(n),其中n是两个序列中任意一个的长度
动态规划法 -
第4题:
阅读下列说明和C代码,回答问题1至问题3,将解答写在答题纸的对应栏内。
【说明】 计算两个字符串x和y的最长公共子串(Longest Common Substring)。 假设字符串x和字符串y的长度分别为m和n,用数组c的元素c[i][j]记录x中前i个字符和y中前j个字符的最长公共子串的长度。c[i][j]满足最优子结构,其递归定义为:

计算所有c[i][j](0 ≤i ≤ m,0 ≤j ≤ n)的值,值最大的c[i][j]即为字符串x和y的最长公共子串的长度。根据该长度即i和j,确定一个最长公共子串。【C代码】(1)常量和变量说明 x,y:长度分别为m和n的字符串 c[i][j]:记录x中前i个字符和y中前j个字符的最长公共子串的长度 max:x和y的最长公共子串的长度 maxi, maXj:分别表示x和y的某个最长公共子串的最后一个字符在x和y中的位置(序号) (2)C程序#include
< stdio.h>#include
< string.h>int c[50][50];int maxi;int maxj;int lcs(char
*x, int m, char *y, int n) { int i, j; int max= 0; maxi= 0; maxj = 0;for ( i=0;
i < =m ; i++) c[i][0] = 0;for (i =1;
i < = n; i++) c[0][i]=0;for (i =1;
i < = m; i++) { for (j=1; j < = n; j++) { if (
(1) ) {c[i][j] = c[i
-1][j -1] + 1;if(max < c[i][j])
{ (2)
; maxi = i; maxj =j; }}else (3)
; } } return max;}void
printLCS(int max, char *x) { int i= 0; if (max == 0) return; for (
(4) ; i < maxi; i++)printf("%c",x[i]);}void main( ){ char* x= "ABCADAB"; char*y= "BDCABA"; int max= 0; int m = strlen(x); int n = strlen(y); max=lcs(x,m,y,n); printLCS(max , x);}
【问题1】(8分)
根据以上说明和C代码,填充C代码中的空(1)~(4)。
【问题2】(4分)
根据题干说明和以上C代码,算法采用了 (5) 设计策略。
分析时间复杂度为 (6) (用O符号表示)。
【问题3】(3分)
根据题干说明和以上C代码,输入字符串x= "ABCADAB’,'y="BDCABA",则输出为 (7) 。答案:解析:【问题1】(8分)答案:(1)x[i-1]= =y[j-1] (2)max=c[i][j](3)c[i][j]=0 (4)i=maxi-max
【问题2】(4分)答案:动态规划、 O(m×n)或O(mn)
【问题3】(3分)答案:AB根据题干和C代码,计算出下表的值。
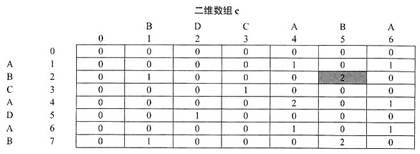
最大值为2。在计算过程中,我们记录第一个最大值,即表中阴影部分元素,因此得到最长公共子串为AB。 -
第5题:
给定两个序列分别为“algorithm”和“glorhythm”。则以下分别为两序列的最长公共子序列和最长公共子串的选项是____
A.gorthm thm
B.thm gorthm
C.glorhthm orthm
D.orthm glorhthm
gorthm thm
