●若用8位机器码表示十进制整数-127,则其原码表示为(9),补码表示为(10)。(9)A.10000000B.11111111C.10111111D.11111110(10)A.10000001B.11111111C.10111110D.11111110
题目
●若用8位机器码表示十进制整数-127,则其原码表示为(9),补码表示为(10)。
(9)A.10000000
B.11111111
C.10111111
D.11111110
(10)A.10000001
B.11111111
C.10111110
D.11111110
相似考题
更多“●若用8位机器码表示十进制整数-127,则其原码表示为(9),补码表示为(10)。(9)A.10000000B.11111111C ”相关问题
-
第1题:
●计算机中十六位浮点数的表示格式为
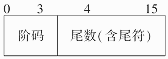
某机器码为1110001010000000,
若阶码为移码且尾数为反码,则其十进制真值为 (7) ;
若阶码为移码且尾数为原码,则其十进制真值为 (8) ;
若阶码为补码且尾数为反码,则其十进制真值为 (9) ;
若阶码为补码且尾数为原码,则其十进制真值为 (10) ,将其规格化后的机器码为 (11) 。
(7)~(10) A.0.078125
B.20
C.20.969375
D.1.25
(11) A.11110101000000
B.1110001010000000
C.1101010100000000
D.11110001010000
正确答案:B,B,A,A,C
【解析】(7)如果阶码为移码,由于阶码是4位二进制整数,设真值为X,根据整数移码定义:[X]移码=23+X(1110)2=(14)10,可求得阶码真值为6。如果尾数为反码,从符号位可判断尾数是正数,根据小数反码定义,正小数的反码就是其自身,可求得尾数的真值为:(0.01010000000)2=(2-2+2-4)=(0.3125)10,根据浮点数定义,该机器码真值为0.3125*26=20。(8)如果阶码为移码,同上,真值为6。如果尾数是原码,从符号位可判断尾数是正数,根据小数原码定义,正小数的原码就是其本身,可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码,由于阶码是4位二进制整数,从符号位判断为负数,设真值为X,根据负整数定义[X]补码=24+X=(1110)2=(14)10,求得阶码的真值为-2。如果尾数为反码,同(7)一样求出尾数的真值为0.3125。这样,该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码,尾数是原码,求出阶码和尾数的真值分别为-2和0.3125,这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理,规定浮点数的尾数部分用纯小数形式表示,当尾数的值不为0时,其绝对值应大于或等于0.5,用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数,可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求,应左移1位,而阶码则应相应地减1,因此规格化处理后的阶码为1101,尾数为010100000000。 -
第2题:
●若用8位机器码表示十进制整数-127,则其原码表示为(12),补码表示为(13)。
(12)A.10000000
B.11111111
C.10111111
D.11111110
(13)A.10000001
B.11111111
C.10111110
D.11111110
正确答案:B,A
-
第3题:
若用8位机器码表示十进制整数-127,则其补码表示为()。A. 10000001
B. 11111111
C. 10111110
D. 11111110答案:A解析: -
第4题:
●若用8位机器码表示十进制整数-127,则其原码表示为(19),补码表示为(20)。
(19)A.10000000
B.11111111
C.10111111
D.11111110
(20)A.10000001
B.11111111
C.10111110
D.11111110
正确答案:B,A
-
第5题:
若用8位机器码表示十进制整数-127,则其原码表示为()A. 10000000
B. 11111111
C. 10111111
D. 11111110答案:B解析:
