设函数f(x)在内连续,其导函数的图形如图所示,则f(x)有(52)。A.一个极小值点和两个极大值点B.两个极小值点和一个极大值点C.两个极小值点和两个极大值点D.三个极小值点和一个极大值点
题目
设函数f(x)在内连续,其导函数的图形如图所示,则f(x)有(52)。
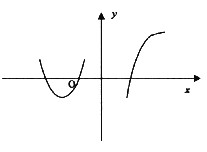
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点
相似考题
更多“设函数f(x)在内连续,其导函数的图形如图所示,则f(x)有(52)。A.一个极小值点和两个极大值点B.两个极小值点和一个极大值点C.两个极小值点和两个极大值点D.三个极小值点和一个极大值点”相关问题
-
第1题:
已知函数f(x,y)在点(0,0)的某个邻域内连续,且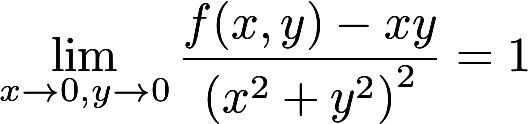 ,则A.点(0,0)不是f(x,y)的极值
,则A.点(0,0)不是f(x,y)的极值
B.点(0,0)是f(x,y)的极大值点
C.点(0,0)是f(x,y)的极小值点
D.根据所给条件无法判断点(0,0)是否为f(x,y)的极值点
答案:A解析:
-
第2题:
设函数f(x)在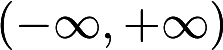 内连续,其导函数的图形如图所示,则f(x)有
内连续,其导函数的图形如图所示,则f(x)有 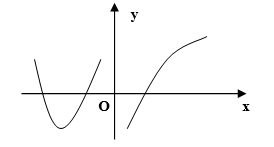 A.一个极小值点和两个极大值点
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点答案:C解析:
-
第3题:
f(x)在(-∞,+∞)内连续,其导数函数f′(x)图形如图所示,则f(x)有( )。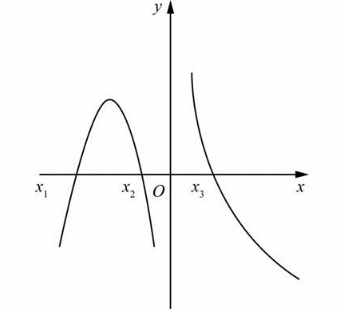 A.一个极小值点和两个极大值点
A.一个极小值点和两个极大值点
B.两个极小值点和两个极大值点
C.两个极小值点和一个极大值点
D.一个极小值点和三个极大值点答案:B解析:由导函数f ′(x)图像可知,函数f(x)有三个驻点x1、x2、x3和一个导数不存在的点0。根据题6解表,原函数f(x)在x1和0处取得极小值,在x2和x3处取得极大值。因此,f(x)有两个极小值点和两个极大值点。
题6解表 函数单调区间表
-
第4题:
 A.一个极小值点和两个极大值点
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点答案:C解析:根据导函数的图形可知,一阶导数为零的点有3个,而x=0是导数不存在的点。三个一阶导数为零的点左右两侧导数符号不一致,必为极值点,且两个极小值点,一个极大值点;在x=0左侧一阶导数为正,右侧一阶导数为负,可见x=0为极大值点,故f(x)共有两个极小值点和两个极大值点。 -
第5题:
 A.是极小值点
A.是极小值点
B.是极大值点
C.不是极值点
D.是否为极值点不定答案:A解析: -
第6题:
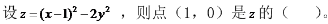 A.极小值点
A.极小值点
B.极大值点
C.最小值点
D.非极值点答案:A解析: -
第7题:
设函数f(x)=(1+x)ex,则函数f(x)( )A.有极小值
B.有极大值
C.既有极小值又有极大值
D.无极值答案:A解析:【考情点拨】本题考查了函数极值的知识点.【应试指导】
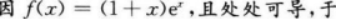

-
第8题:
设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )《》( )A.不是f(x,y)的连续点
B.不是f(x,y)的极值点
C.是f(x,y)的极大值点
D.是f(x,y)的极小值点答案:D解析:
-
第9题:
点(2,-2)是函数f(x,y)=x(4―x)―y(y+4)的()。
- A、极小值点
- B、非极值点
- C、非极值驻点
- D、极大值点
正确答案:D -
第10题:
单选题设f(x)在x=0处满足f′(0)=f″(0)=…=f(n)(0),f(n+1)(0)>0,则( )。A当n为偶数时,x=0是f(x)的极大值点
B当n为偶数时,x=0是f(x)的极小值点
C当n为奇数时,x=0是f(x)的极大值点
D当n为奇数时,x=0是f(x)的极小值点
正确答案: C解析:
此题可用举例法判断。当n=1时(即n为奇数),f′(0)=0,f″(0)>0。由f″(0)>0知f′(x)在x=0处单调增加。又f′(0)=0,x<0时f′(x)<0;x>0时f′(x)>0。因此f(x)在x=0点处取得极小值。
当n=2时(即n为偶数),f′(0)=f″(0)=0,f‴(0)>0。由f‴(0)>0知,f″(x)在x=0处单调增加。因f″(0)=0,故f′(x)在x=0附近先减小后增加。f′(0)=0,故f(x)在x=0点处单调。因此x=0既不是f(x)的极大值也不是它的极小值。综上所述D项正确。 -
第11题:
单选题点(2,-2)是函数f(x,y)=x(4―x)―y(y+4)的()。A极小值点
B非极值点
C非极值驻点
D极大值点
正确答案: D解析: 暂无解析 -
第12题:
单选题点x=2是函数y=x(x-4)+3的()。A极大值点
B极小值点
C非驻点
D非极值驻点
正确答案: D解析: 暂无解析 -
第13题:
设函数y-f(x)连续,除x=a外f''(x)均存在。一一阶导函数y'=f(x)的图形如下,则y=f(x)
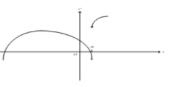 A.有两个极大值点,一个极小值点,一个拐点
A.有两个极大值点,一个极小值点,一个拐点
B.有一个极大值点,一个极小值点,两个拐点
C.有一个极大值点,一个极小值点,一个拐点
D.有一个极大值点,两个极小值点,两个拐点答案:D解析:




-
第14题:
设函数f(x)在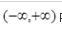
内连续,其导函数的图形如图所示,则f(x)有( )。 A.一个极小值点和两个极大值点
A.一个极小值点和两个极大值点
B.两个极小值点和一个极大值点
C.两个极小值点和两个极大值点
D.三个极小值点和一个极大值点答案:C解析:答案与极值点个数有关,而可能的极值点应是导数为零或导数不存在的点,共4个,是极大值点还是极小值点可进一步由取极值的第一或第二充分条件判定.根据导函数的图形可知,一阶导数为零的点有3个,而x=0则是导数不存在的点.三个一阶导数为零的点左右两侧导数符号不一致,必为极值点,且两个极小值点,一个极大值点;在x=0左侧一阶导数为正,右侧一阶导数为负,可见x=0为极大值点,故f(x)共有两个极小值点和两个极大值点,应选(C)。 -
第15题:
对于函数f(x,y)=xy,原点(0,0)( )。A.不是驻点
B.是驻点但非极值点
C.是驻点且为极小值点
D.是驻点且为极大值点答案:B解析:驻点是指函数f(x,y)一阶偏导数均等于零的点。对于函数f(x,y)=xy,fx=y,fy=x,则fx(0,0)=fy(0,0)=0。因此,原点(0,0)是函数的驻点。
设函数f(x,y)在点P0(x0,y0)的某个邻域内具有二阶连续偏导数,且P0(x0,y0)是驻点。设A=fxx(x0,y0),B=fxy(x0,y0),C=fyy(x0,y0),则:
①当B2-AC<0时,点P0(x0,y0)是极值点,且当A<0时,点P0(x0,y0)是极大值;当A>0时,点P0(x0,y0)是极小值点;
②当B2-AC>0时,点P0(x0,y0)不是极值点;
③当B2-AC=0时,点P0(x0,y0)有可能是极值点也有可能不是极值点。
对于函数f(x,y)=xy,A=fxx(x0,y0)=0,B=fxy(x0,y0)=1,C=fyy(x0,y0)=0,则B2-AC=1>0。因此,原点(0,0)不是极值点。
综上,原点(0,0)是驻点但非极值点。 -
第16题:
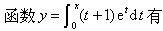 A.极小值点x=-1
A.极小值点x=-1
B.极大值点x=-1
C.极小值点x=0
D.极大值点x=0答案:A解析: -
第17题:
设函数y=f(x)的导函数,满足f′(一1)=0,当x<-l时,f′(x)<0;当x>-l时,f′(x)>0.则下列结论肯定正确的是( ).《》( )A.x=-1是驻点,但不是极值点
B.x=-1不是驻点
C.x=-1为极小值点
D.x=-1为极大值点答案:C解析: -
第18题:
函数y(x)的导函数f(x)的图象如图所示,Xo=-1,则( )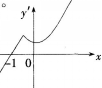 A、X。不是驻点
A、X。不是驻点
B、x。是驻点,但不是极值点
C、x。是极小值点
D、 X。极大值点答案:C解析:由图可知
f,+(‰)>0,一(‰)<0且f(x)在x连续可导,故xo为极小值点。 -
第19题:
设函数f(x)在[0,b]连续,在(a,b)可导,f′(x)>0.若f(a)·f(b)<0,则y=f(x)在(a,b)().A.不存在零点
B.存在唯一零点
C.存在极大值点
D.存在极小值点答案:B解析:由于f(x)在[a,b]上连续f(z)·fb)<0,由闭区间上连续函数的零点定理可知,y=f(x)在(a,b)内至少存在一个零点.又由于f(x)>0,可知f(x)在(a,b)内单调增加,因此f(x)在(a,b)内如果有零点,则至多存在一个.综合上述f(x)在(a,b)内存在唯一零点,故选B. -
第20题:
 A.当n为偶数时,x=0是f(x)的极大值点
A.当n为偶数时,x=0是f(x)的极大值点
B.当n为奇数时,x=0是f(x)的极小值点
C.当n为奇数时,x=0是f(x)的极大值点
D.当n为偶数时,x=0是f(x)的极小值点答案:D解析: -
第21题:
点x=2是函数y=x(x-4)+3的()。
- A、极大值点
- B、极小值点
- C、非驻点
- D、非极值驻点
正确答案:B -
第22题:
单选题设确定了函数y=g(x),则( )。Ax=0是函数y=g(x)的驻点,且是极大值点
Bx=0是函数y=g(x)的驻点,且是极小值点
Cx=0不是函数y=g(x)的驻点
D存在x=0的一个小邻域,y=g(x)是单调的
正确答案: B解析:
g′(x)=dy/dx=(dy/dt)·(dt/dx)。dy/dt=2t/(1+t2),dx/dt=1/(1+t2)。故y′(x)=2t。又x=0时,t=0,g′(x)=0;t<0时,x<0,g′(x)<0,g(x)单调减少;t>0时,x>0,g′(x)>0,g(x)单调增加。故x=0是y=g(x)的驻点,且是极小值点。 -
第23题:
单选题设函数z=f(x,y)的全微分为dz=xdx+ydy,则点(0,0)( )。A不是f(x,y)的连续点
B不是f(x,y)的极值点
C是f(x,y)的极大值点
D是f(x,y)的极小值点
正确答案: A解析:
函数的全微分为dz=xdx+ydy,则∂z/∂x=x,∂z/∂y=y,故∂2z/∂x2|(0,0)=1=A,∂2z/∂x∂y|(0,0)=0=B,∂2z/∂y2|(0,0)=1=C,又∂z/∂x|(0,0)=0,∂z/∂y|(0,0)=0,则B2-AC=-1<0,A>0。故(0,0)是函数f(x,y)的极小值点。
