若将有限状态自动机(DFA)识别的0、1符号串看作二进制数，则(6)识别的是能被十进制数3整除的正整数，(7)是与该自动机等价的正规式。A．B．C．D．
题目
若将有限状态自动机(DFA)识别的0、1符号串看作二进制数，则(6)识别的是能被十进制数3整除的正整数，(7)是与该自动机等价的正规式。
A．
B．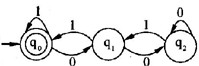
C．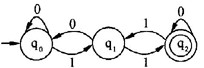
D．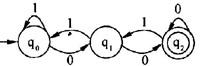
相似考题
更多“ 若将有限状态自动机(DFA)识别的0、1符号串看作二进制数，则(6)识别的是能被十进制数3整除的正整数，(7)是与该自动机等价的正规式。A．B．C．D． ”相关问题
-
第1题：
如图3-1所示为一确定有限自动机(DFA)的状态转换图，与该自动机等价的正规表达式是(1)，图中的(2)是可以合并的状态。
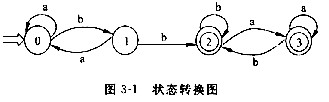
A．(a|b)* bb(a*b*)*
B．(a|b)*bba*|b*
C．(a*b*)bb(a|b)*
D．(a*|b*)*bb(a*|b*)
正确答案：A
解析：在状态转换图中，每一个结点代表一个状态，其中双圈是终结状态。该题实际上是一个简化确定有限自动机(DFA)的过程，一个确定有限自动机可以通过消除多余状态和合并等价状态而转换成一个最小的与之等价的有限自动机。
首先介绍2个概念：最小状态DFA和等价状态。
最小状态DFA必须满足以下2个条件。
(1)没有多余状态(死状态)：多余状态从该自动机的开始状态出发，任何输入串都不能到达的那个状态。
(2)没有2个状态是互相等价(不可区别)。
2个状态s和t如果同时满足下列2个条件，就称s和t是等价的。
(1)一致性：同是终态或同是非终态。
(2)蔓延性：从s出发读人某个a和从t出发读入某个a到达的状态等价。
本题的简化过程如下：
首先，将图中状态分为终态和非终态2个子集即({0,1},{2,3})，再进行子集划分，观察第一个子集{0,1}，输入b后，状态0转换为状态1，而状态1转换为状态2。因此{1}和{2}中的状态是可区别的。
由于状态2,3输入字符a得到相同的结果3，输入字符b得到相同结果2，所以子集 {2,3}是不可区别的。从而得到新的划分：({0}，{1}，{2，3})，因此，(2)空的正确答案为B。
重复子集划分步骤，发现新的状态无法再次划分。
所以，本题中2，3状态可以消除3状态，得到新的状态转换图如图3-2所示。
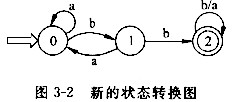
由图3-2可知终态2可以转换为正规表达式(a|b)*，同时必须输入连续2个b字符，才能完成0状态到终态2的转换，所以结果正规表达式必为形如“...bb(a|b)*”的字符串。又因为0和1之间由b和a轮回输入，可以表示为(ba)*，同时，状态0上输入a又回到自身，可以表示为a*。因此，(1)空的正确答案应该为(a*b*)*bb(a|b)*，根据正规式之间的代数性质，(a*b*)*bb(a|b)*与(a|b)*bb(a*b*)*等价。 -
第2题：
某一确定性有限自动机(DFA)的状态转换图如图6-5所示，令d=0|1|2|…|9，则以下字符串中，不能被该DFA接受的是(3)，与该DFA等价的正规式是(4)。 (其中，ε表示空字符)
①3857
②1.2E+5
③-123
④.576E10
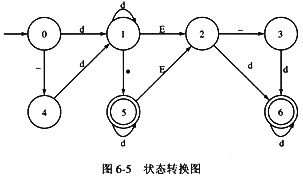
A．①、②、③
B．①、②、④
C．②、③、④
D．①、②、③、④
正确答案：B
-
第3题：
某一非确定性有限自动机(NFA)的状态转换图如下图所示，与该NFA等价的正规式是(28)，与该NFA等价的DFA是(29)。
A．0*|(0|1)0
B．(0|10)*
C．0*((0|1)0)*
D．0*(10)*
正确答案：B
解析：根据分析题目中给出的状态转换图可知，该NFA可识别空串以及任意数目0组成的串，但若出现1，则其后至少要有1个0才能到达终态，因此，该自动机识别的串等价于正规式(0|10)*。 -
第4题：
某一确定有限自动机(DFA)的状态转换图如下图，与该自动机等价的正规表达式是(28)，图中(29)是可以合并的状态。
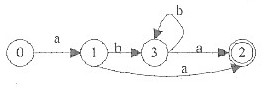
(56)
A．ab*a
B．ablab*a
C．a*b*a
D．aa*lb*a
正确答案：A
-
第5题：
已知一不确定的有限自动机(NFA)如图6-6所示，采用子集法将其确定化为DFA的过程如表6-1所示。
状态集T1中不包括编号为(58)的状态；状态集T2中的成员有(59)；状态集乃等于(60)；该自动机所识别的语言可以用正则式(61)表示。
A．2
B．4
C．3
D．5
正确答案：A
-
第6题：
设有穷自动机的状态转换图如下图，该自动机识别的语言是(29)。
A．∑={0，1)上的所有符号串的集合，但不包含空符号串
B．空符号串集合
C．∑={0，1)上的所有符号串的集合，包含空符号串
D．空集合
正确答案：D
解析：因为从有穷自动机的开始状态A出发，无法到达终止状态B，所以该有穷自动机不能接受任何符号串，即该有穷自动机识别的语言为空集合。 -
第7题：
某一确定有限自动机(DFA)的状态转换图如图2-1所示，该DFA接受的字符串集是(7)，与之等价的正规式是(8)。
A．以1开头的二进制代码串组成的集合
B．以1结尾的二进制代码串组成的集合
C．包含偶数个0的二进制代码串组成的集合
D．包含奇数个0的二进制代码串组成的集合
正确答案：C
-
第8题：
某一非确定性有限自动机(NFA)的状态转换图如图2-6所示，与该NFA等价的正规式是(12)，与该NFA等价的DFA是(13)。
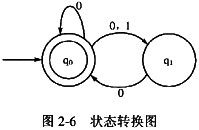
A．0*｜(0｜1)0
B．(0｜10)*
C．0*[(0｜1)0]*
D．0*(10)*
正确答案：B
-
第9题：
下图是一个有限自动机的状态转换图（A为初态、C为终态），该自动机识别的字符串集合可用正规式（ ）来表示。
A.（1|2）*00
B.0（1|2）*0
C.（0|1|2）*
D.00（1|2）*答案：B解析：一个有限自动机所识别的语言是从开始状态到终止状态所有路径上的字符串的集合。要判断一个字符串能否被指定的自动机识别，就看在该自动机的状态图中能否找到一条从开始状态到达终止状态的路径，且路径上的字符串等于需要识别的字符串。从图中看，首先要识别字符0，然后最终要识别的也是字符0，中间识别1或者2，可以0次或者无穷次。 -
第10题：
某一非确定性有限自动机（NFA）的状态转换图如下图所示，与该NFA等价的正规式是（请作答此空），与该NFA等价的DFA是（ ）。
A.0*|（0|1）0
B.（0|10）*
C.0*（（011）0）*
D.0*（10）*答案：B解析： -
第11题：
下图所示为一个不确定有限自动机的状态转换图，与该NFA等价的DFA是（ ）。
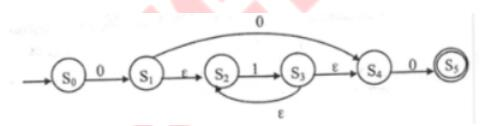
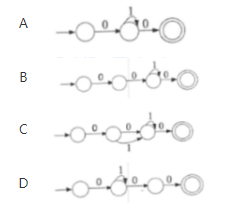答案：C解析：本题可以直接以实例方式排除错误选项。本题给出的NFA，能够识别字符串000,010等，以这两个字符串为例进行分析。与之等价的DFA，也必须能够识别这样的串。A选项不能识别000，B选项不能识别010，D选项不能识别010.只有C选项能够同时识别这2个串，因此本题选择C选项 -
第12题：
某确定的有限自动机（DFA）的状态转换图如下图所示（0 是初态，4 是终态），则该 DFA能识别（49）。
A.aaab
B.abab
C.bbba
D.abba答案：A解析：将选项分别带入判断。 -
第13题：
已知一不确定的有限自动机(NFA)如图2-8所示，采用子集法将其确定化为DFA的过程如表2-1所示。
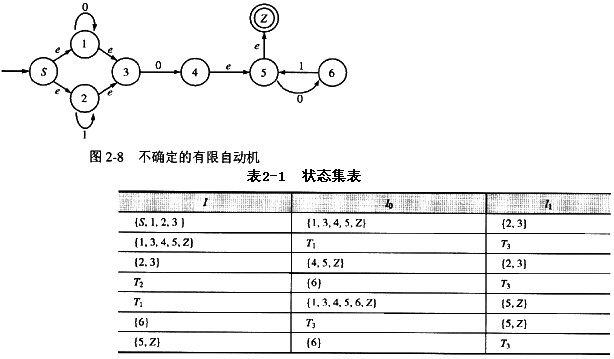
状态集T1中不包括编号为(23)的状态；状态集T2中的成员有(24)：状态集T3等于(25)；该自动机所识别的语言可以用正规式(26)表示。
A．2
B．4
C．3
D．5
正确答案：A
-
第14题：
某一非确定性有限自动机(NFA)的状态转换图如图6-1所示，该NFA等价的正规式是(1)，与该NFA等价的DFA是(2)。
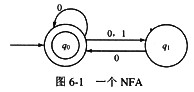
A．0*|(0|1)0
B．(0|10)*
C．0*((0|1)0)*
D．0*(10)*
正确答案：B
-
第15题：
某一确定有限自动机(DFA)的状态转换图如下，与该自动机等价的正规表达式是(28)，图中(29)是可以合并的状态。
(42)
A．(a|ba)*bb(a*b*)*
B．(a|ba)*bba*|b*
C．(a*|b*)bb(a|b)*
D．(a|b*)*bb(a*|b*)
正确答案：A
-
第16题：
●下图所示为一个有限自动机（其中，A是初态、C是终态），该自动机识别的语言可用正规式(48)表示。
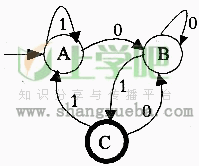
(48)
A. (0|1)*01
B．1*0*10*1
C．1*(0)*01
D.1*(0|10)*1*
正确答案：A
-
第17题：
图2-7为一确定有限自动机(DFA)的状态转换图，与该自动机等价的正规表达式是(14)，图中的(15)是可以合并的状态。
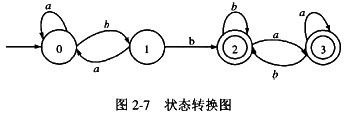
A．[a｜(ba)]*bb(a*b*)*
B．(a｜b)*bba*｜b*
C．(a*b*)bb(a｜b)*
D．(a｜b)*bb(a*｜b*)*
正确答案：A
-
第18题：
某一确定有限自动机(DFA)的状态转换图如下图所示，该DFA接受的字符串集是(28)，与之等价的正规式是(29)。
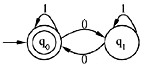
A．以1开头的二进制代码串组成的集合
B．以1结尾的二进制代码串组成的集合
C．包含偶数个0的二进制代码串组成的集合
D．包含奇数个0的二进制代码串组成的集合
正确答案：C
解析：分析题日中给出的状态转换图可知，状态q0为唯一的终态，因此该DFA可识别空串。以一个。离开状态q0然后再以一个0返回q0，因此，该自动机识别的串是包含偶数个0的二进制代码串。正规式中的运算符“|”、“.”、“*”分别称为“或”、“连接”和“闭包”。在正规式的书写中，连接运算符“.”可省略。运算的优先级从高到低顺序排列为：“*”、“.”、“|”。正规式1*0(0|1)*、((0|1*0)*1*)*、1*((0|1)0)*都没布表示出偶数个零的特点，因此包含偶数个0的二进制代码串的正规式为(1*(01*0)*)*。 -
第19题：
某一确定性有限自动机(DFA)的状态转换图如图2-2所示，令d=0｜1｜2｜…19，则以下字符串中，不能被该DFA接受的是(9)，与该DFA等价的正规式是(10)。(其中，ε表示空字符。)
A．①②③
B．①②④
C．②③④
D．①②③④
正确答案：B
-
第20题：
以下关于下图所示有限自动机的叙述中．不正确的是 (49) 。
A.该自动机识别的字符串中a不能连续出现
B.该自动机识别的字符串中b不能连续出现
C.该自动机识别的非空字符串必须以a结尾
D.该自动机识别的字符串可以为空串
正确答案：A
本题考查程序语言基础知识。自动机识别字符串的过程是：从初态出发，根据字符串的当前字符实现状态转移。如果存在从初态到终态的状态转移路径与字符串中的各个字符相匹配，那么就说该自动机可以识别该字符串。题中所给自动机的初态和终态都是编号为1的状态，从其状态图可知，从状态1开始，识别出字符“a”时仍然转移到状态1，而识别出字符"b”时才离开状态1进入状态2，状态2仅对字符“a”有状态转移，且转回状态1。因此，该自动机识别的字符串仅包含a、b字符，但是字符"b”不能连续出现，连续出现“a”是可以的。 -
第21题：
某非确定的有限自动机（NFA）的状态转换图如下图所示（q0既是初态也是终态），与该NFA等价的确定的有限自动机（DFA）是 （ ） 。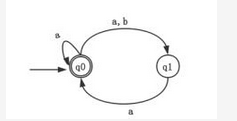
答案：A解析：本题考查有限自动机这一知识点。容易看出，能被题中不确定的有限自动机接受的符号串有两种情形，一种是???表示的符号串，另一种是(ba)?符号串。在四个选项中，只有A选项的有限自动机能同时接受???和(ba)?这两种符号串，故本题选择A选项。 -
第22题：
某一非确定性有限自动机（NFA）的状态转换图如下图所示，与该NFA等价的正规式是（ ），与该NFA等价的DFA是（请作答此空）。
答案：A解析： -
第23题：
某一确定有限自动机(DFA.的状态转换图如下图所示，该DFA接受的字符串集是 ( ) ，与之等价的正规式是 (请作答此空) 。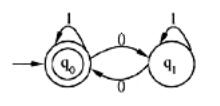
A.1*0(0|1)*
B.((0|1*0)*1*)*
C.1*((0|1)0)*
D.(1*(01*0)*)*答案：D解析：分析题日中给出的状态转换图可知，状态q0为唯一的终态，因此该DFA可识别空串。以一个。离开状态q0然后再以一个0返回q0，因此，该自动机识别的串是包含偶数个0的二进制代码串。正规式中的运算符“|”、“•”、“*”分别称为“或”、“连接”和“闭包”。在正规式的书写中，连接运算符“•”可省。运算的优先级从高到低顺序排列为：“*”、“•”、“|”。正规式1*0(0|1)*、((0|1*0)*1*)*、1*((0|1)0)*都没布表示出偶数个零的特点，因此包含偶数个0的二进制代码串的正规式为(1*(01*0)*)*。