某工厂计划生产甲、乙两种产品。生产每套产品所需的设备台时、A、B两种原材料和可获利润以及可利用资源数量如下表所示。则应按（）方案来安排计划以使该工厂获利最多。A.生产甲2套，乙3套B.生产甲1套，乙4套C.生产甲3套，乙4套D.生产甲4套，乙2套

题目

某工厂计划生产甲、乙两种产品。生产每套产品所需的设备台时、A、B两种原材料和可获利润以及可利用资源数量如下表所示。则应按（）方案来安排计划以使该工厂获利最多。

A.生产甲2套，乙3套

B.生产甲1套，乙4套

C.生产甲3套，乙4套

D.生产甲4套，乙2套

相似考题

1.● 某工厂生产甲、乙两种产品，生产 1 公斤甲产品需要煤 9 公斤、电 4 度、油 3公斤，生产 1 公斤乙产品需要煤 4 公斤、电 5 度、油 10 公斤。该工厂现有煤 360 公斤、电 200 度、油 300 公斤。已知甲产品每公斤利润为 7 千元，乙产品每公斤利润为 1.2 万元，为了获取最大利润应该生产甲产品（66）公斤，乙产品（67）公斤。（66）A.20B.21C.22D.23（67）A.22B.23C.24D.25

2.某工厂拥有A.B.C三种类型的设备，生产甲、乙两种产品，每件产品在生产中需要使用的机时数，每件产品可以获得的利润，以及三种设备可利用的机时数见下表:求:(1)线性规划模型(2)利用单纯形法求最优解

3.某工厂生产甲、乙两种主要设备，这两种设备均需要逐台按序经过两条装配线进行装配，有关数 据与可获利润如表7-2所示。只要每周合理安排这两条装配线的生产顺序，该工厂可能获得的最大利润是__________万元。(注：第一装配线和第二装配线同时接通电源，且连续工作)。

4.某工厂生产两种产品S和K，受到原材料供应和设备加工工时的限制。单件产品的利润、原材料消耗及加工工时如下表所示。为获得最大利润，S应生产______件。A．7B．8C．9D．10

更多“某工厂计划生产甲、乙两种产品。生产每套产品所需的设备台时、A、B两种原材料和可获利润以及可利用资 ”相关问题

  • 第1题：

    某企业生产甲、乙两种产品，按原材料定额消耗量比例分配原材料费用。2007年元月甲、乙两种产品共耗用A原材料6 000千克，每千克单价1．44元；当月生产甲产品i 200件，单件甲产品消耗A材料的消耗定额为3千克；当月生产乙产品800件，单件乙产品消耗A材料的消耗定额为1．5千克；则当月甲产品应分配原材料费用（ ）元。

    A．5 184

    B．1 728

    C．6 480

    D．2 160


    正确答案：B
    16 000×1．44／(1 200×3+800×1．5)×1 200×3=6 480(元)

  • 第2题：

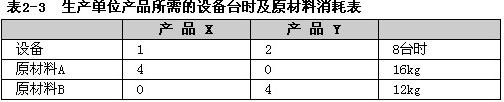
    某企业在计划期内要同时生产X、Y两种产品。已知生产单位产品所需的设备台及A、B两种原材料的消耗如表2-3所示。该企业每生产一件产品X可获利2000元，每生产一件产品Y可获利3000千元。合理安排计划能使该企业生产获取的最大利润是(63)元。

    A．12000

    B．13000

    C．14000

    D．16000


    正确答案：C
    解析：设x1，x2分别表示在计划期内产品X、Y的产量，则可得到如表2-10的求解过程。表2-10反映的生产计划问题可用数学模型表示为：目标函数：maxz=2x1+3x2约束条件：x1+2x2≤8；4x1≤16；4x2≤12；x1，x20求解以上约束条件可得，最大利用设备时的方案有2种，即(x1=2，x2=3)和(x1=4，x2=2)，但仅当x1=4、x2=2时，该企业生产所获取的最大利润是14000元。

  • 第3题：

    某企业生产甲、乙两种产品，已知生产每吨甲产品要用A原料3吨、B原料2吨；生产每吨乙产品要用A原料1吨、B原料3吨。销售每吨甲产品可获得利润5万元，每吨乙产品可获得利润3万元，该企业在一个生产周期内消耗A原料不超过13吨，B原料不超过18吨，那么该企业可获得最大利润是

    A. 12万元 B. 20万元 C. 25万元 D. 27万元


    正确答案：D

  • 第4题：

    某工厂生产甲和乙两种产品。已知生产1件甲产品可获利1000元,消耗a和b材料分别为2千克、3千克；生产1件乙产品可获利1700元,消耗a和b材料分别为5千克、4千克。若有a和b材料分别为200千克、240千克,则生产甲、乙两种产品能取得的最大利润是：

    A.85200元
    B.86278元
    C.85900元
    D.86600元

    答案：C
    解析：
    第一步，本题考查统筹推断类。
    第二步，设生产甲产品x件，生产乙产品y件时，获得的利润最大。当两种材料都尽量用尽时，是最优情况。可列方程组：2x＋5y＝200①；3x＋4y＝240②，联立解得，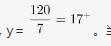

    当y取17时，x最大可取57，此时总利润为57×1000＋17×1700＝85900（元），当y取18时，x最大可取55，此时总利润为55×1000＋18×1700＝85600（元），显然y取17，x取57时，总利润最大，为85900元。
    因此，选择C选项。

  • 第5题：

    某工厂生产甲、乙两种产品，生产1公斤甲产品需要煤9公斤、电4度、油3公斤，生产1公斤乙产品需要煤4公斤、电5度、油10公斤。该工厂现有煤360公斤、电200度、油300公斤。已知甲产品每公斤利润为7千元，乙产品每公斤利润为1.2万元，为了获取最大利润应该生产甲产品 （请作答此空） 公斤，乙产品 （ ） 公斤。

    A.20
    B.21
    C.22
    D.23

    答案：A
    解析：
    设x1为甲产品生产量，x2为乙产品生产量。对该问题求解最优方案可以由下列数学模型描述：max z=7x1+12x29x1+4x2≤3604x1+5x2≤2003x1+10x2≤300x1≥0，x2≥0求解得x1=20，x2=24。

  • 第6题：

    某工厂生产甲、乙两种产品，生产1公斤甲产品需要煤9公斤、电4度、油3公斤，生产1公斤乙产品需要煤4公斤、电5度、油10公斤。该工厂现有煤360公斤、电200度、油300公斤。已知甲产品每公斤利润为7千元，乙产品每公斤利润为1.2万元，为了获取最大利润应该生产甲产品 （ ） 公斤。

    A.20
    B.21
    C.22
    D.23

    答案：A
    解析：
    设x1为甲产品生产量，x2为乙产品生产量。对该问题求解最优方案可以由下列数学模型描述：max z=7x1+12x29x1+4x2≤3604x1+5x2≤2003x1+10x2≤300x1≥0，x2≥0求解得x1=20

  • 第7题：

    某工厂计划生产甲、乙两种产品。生产每套产品所需的设备台时、A、B两种原材料和可获取利润以及可利用资源数量如下表所示。则应按（ ）方案来安排计划以使该工厂获利最多。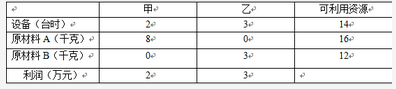

    A.生产甲2套，乙3套
    B.生产甲1套，乙4套
    C.生产甲3套，乙4套
    D.生产甲4套，乙2套

    答案：B
    解析：
    设甲生产X套，乙生产Y套，则有：2X+3Y≤14； X≤2； Y≤4；同时要满足利润最大，只有X取1，Y取4时利润最大是14万元。

  • 第8题：

    某厂编号为I、II、III的三种产品分别经过A、B、C三种设备加工，已知生产各种产品每件所需的设备台时，各种设备的加工能力（台时）及每件产品的预期利润见下表。

    适当安排生产计划可获得最大总利润 （ ） 元。

    A.2000/3
    B.2100/3
    C.2200/3
    D.2250/3

    答案：C
    解析：
    按Ⅰ、Ⅱ、Ⅲ排列时间效率：A为1 1 1 ；B为1/10 1/4 1/5；C为1/2 1/2 1/6。利润率，则A为10 6 4 ；B为1 1.5 0.8；C为5 3 2/3，所以第3种产品利润最低，不占用时间，因此推出x+y<=100，10x+4y<=600，最后求得x=100/3，y=200/3，利润为10x+6y=2200/3。

  • 第9题：

    某工厂生产甲、乙两种产品，生产1公斤甲产品需要煤9公斤、电4度、油3公斤，生产1公斤乙产品需要煤4公斤、电5度、油10公斤。该工厂现有煤360公斤、电200度、油300公斤。已知甲产品每公斤利润为7千元，乙产品每公斤利润为1.2万元，为了获取最大利润应该生产乙产品 （ ） 公斤。

    A.22
    B.23
    C.24
    D.25

    答案：C
    解析：
    设x1为甲产品生产量，x2为乙产品生产量。对该问题求解最优方案可以由下列数学模型描述：max z=7x1+12x29x1+4x2≤3604x1+5x2≤2003x1+10x2≤300x1≥0，x2≥0求解得x2=24。

  • 第10题：

    某工厂于2017年4月，用A原材料经过同一生产过程同时生产出甲、乙两种联产品。假定该月无期初期末在产品，本月共生产甲产品300吨，乙产品200吨。该月生产发生的联合成本分别为：原材料为5000元，直接人工费为2000元，制造费用为3500元。甲产品每吨售价50元，乙产品每吨售价60元，产品均已售出。乙产品的售价系数为（）。

    • A、1.2
    • B、0.83
    • C、0.67
    • D、0.4

    正确答案:A

  • 第11题：

    单选题
    某公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗A原料1千克、B原料2千克：生产乙产品1桶需耗A原料2千克、B原料1千克。每桶甲产品的利润是300元，每桶乙产品的利润是400元。公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12干克.通过合理安排生产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是：
    A

    1800元

    B

    2400元

    C

    2800元

    D

    3100元


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    某工厂生产甲和乙两种产品，甲产品的日产量是乙产品的1.5倍。现工厂改进了乙产品的生术技术，在保证产量不变的前提下，其单件产品生产能耗降低了20%，而每日工厂生产甲和乙两种产品的总能耗降低了10%。则在改进后，甲、乙两种产品的单件生产能耗之比为？
    A

    2：3

    B

    3：4

    C

    4：5

    D

    5：6


    正确答案： B
    解析： 暂无解析

  • 第13题：

    ● 某工厂生产两种产品S和K，受到原材料供应和设备加工工时的限制。单件产品利润、原材料消耗及加工工时如下表。为获得最大利润，S应生产（68）件。

    （68）A. 7 B. 8 C. 9 D. 10


    正确答案：B

  • 第14题：

    某厂准备生产甲、乙、丙三种产品，生产每件产品所需的A、B两种原料数量，能获得的利润，以及工厂拥有的原料数量如下表：

    根据该表，只要安排好生产计划，就能获得最大利润（ ）万元。

    A.25

    B.26

    C.27

    D.28


    正确答案：C

  • 第15题：

    某工厂生产甲、乙两种产品，生产1公斤甲产品需要煤9公斤、电4度、油3公斤，生产1公斤乙产品需要煤4公斤、电5度、油10公斤。该工厂现有煤360公斤、电200度、油300公斤。已知甲产品每公斤利润为7千元，乙产品每公斤利润为1.2万元，为了获取最大利润应该生产甲产品(1)公斤，乙产品(2)公斤。

    (1)

    A．20

    B．21

    C．22

    D．23


    正确答案：A

  • 第16题：

    某厂准备生产甲、乙、丙三种产品，生产每件产品所需的A、B两种原料数量，能获得的利润，以及工厂拥有的原料数量如下表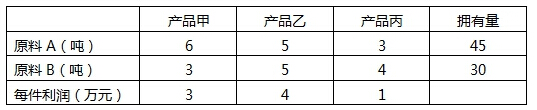

    根据该表，只要安排好生产计划，就能获得最大利润（54）万元。

    A.25
    B.26
    C.27
    D.28

    答案：C
    解析：
    设该厂计划生产甲x件，乙y件，丙z件，则有线性规划模型：

    Max S=3x+4y+z

    6x+5y+3z≤45

    3x+5y+4z≤30

    xyz≥0

    线性规划问题的最优解必然在可行解区的顶点处达到。

    因此，在x=5, y=3, z=0时能获得最大利润27万元。

    可以通过坐标图解答。

  • 第17题：

    某电池厂生产甲，乙两种型号，产品（单位:万个）,这两种产品都需要设备和A、B2种原材料。利润与资源限制条件如表所示，为了获得最大的利润，该电池厂每天生产的甲产品的数量应为1万个，此时该企业每天的利润为（ ）万元。

    A.20
    B.22
    C.24
    D.26

    答案：D
    解析：
    线性方程，必考内容。

  • 第18题：

    某电池厂生产甲，乙两种型号，产品（单位:万个）,这两种产品都需要设备和A、B2种原材料。利润与资源限制条件如表所示，为了获得最大的利润，该电池厂每天生产的甲产品的数量应为（）万个，此时该企业每天的利润为（）万元。

    A.1
    B.2
    C.3
    D.4

    答案：A
    解析：
    线性方程，必考内容。

  • 第19题：

    某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数如表所示：

    则公司可以获得的最大利润是 （ ） 万元。

    A.21
    B.34
    C.39
    D.48

    答案：B
    解析：
    设生产的产品I为x吨，产品II为y吨，则：1x + 1y ? 44x + 3y? 121x + 3y? 6解上述方程可知，x=2，y=4/3。因此，最大利润是：9 ? 2 + 12 ? 4/3 = 34

  • 第20题：

    某企业需要采用甲、乙、丙三种原材料生产Ⅰ、Ⅱ两种产品。生产两种产品所需原材料数量、单位产品可获得利润以及企业现有原材料数如表所示：取得最大利润时，原材料 （ ） 尚有剩余。

    A.甲
    B.乙
    C.丙
    D.乙和丙

    答案：A
    解析：
    设生产的产品I为x吨，产品II为y吨，则：1x + 1y ? 44x + 3y? 121x + 3y? 6解上述方程可知，x=2，y=4/3。因此，最大利润是：9 ? 2 + 12 ? 4/3 = 34原料“甲”还剩余：4-2-1.3333

  • 第21题：

    某工厂生产两种产品S和K，受到原材料供应和设备加工工时的限制。单件产品的利润、原材料消耗及加工工时如下表。为获得最大利润，S应生产 （ ） 件。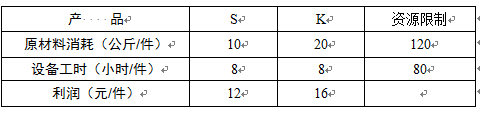

    A.7
    B.8
    C.9
    D.10

    答案：B
    解析：
    设利润为Z，为了获得最大利润，S应生产X1件，K应生产X2件。对该问题求解最优方案可以由下列数学模型描述： Max z=12X1+16X210X1+20X2≤1208X1+8X2≤80 X1≥0，X2≥0

  • 第22题：

    企业利用现有设备可生产甲、乙两种产品，甲、乙两种产品的变动生产成本差额为6000元／月，预计销售收入差额为5900元／月，则该企业应生产（）产品。

    • A、甲
    • B、乙
    • C、甲、乙均行
    • D、甲、乙均不行

    正确答案:B

  • 第23题：

    问答题
    某企业生产甲、乙两种产品共同耗用A种原材料6000公斤，每公斤计划单价6元。本月产量为：甲产品500件，乙产品400件。单件产品原材料消耗定额为：甲产品6公斤，乙产品5公斤。原材料成本差异率为1% 。按定额消耗量比例分配甲、乙产品的材料费用。

    正确答案： 原材料定额消耗量：
    甲产品：500×6=3000（公斤）
    乙产品：400×5=2000（公斤）
    材料费用分配率=6000×6/（3000+2000）=7.2
    两种产品应分配的材料计划成本：
    甲产品：7.2×3000=21600（元）
    乙产品：7.2×2000=14400（元）
    应负担的材料成本差异：
    甲产品=21600×1%= 216（元）
    乙产品=14400×1%= 144（元）
    解析： 暂无解析

  • 第24题：

    单选题
    公司生产甲、乙两种桶装产品。已知生产甲产品1桶需耗A原料1千克、B原料2千克：生产乙产品1桶需耗A原料2千克、B原料1千克。每桶甲产品的利润是300元，每桶乙产品的利润是400元。公司在生产这两种产品的计划中，要求每天消耗A、B原料都不超过12千克。通过合理安排坐产计划，从每天生产的甲、乙两种产品中，公司共可获得的最大利润是：
    A

    1800元

    B

    2400元

    C

    2800元

    D

    3100元


    正确答案： C
    解析：

相关内容