阅读以下说明和C函数代码，回答问题并将解答写在对应栏内。【说明】著名的菲波那契数列定义式为f1=1 f2=1 fn=fn-1+fn-2 (n=3，4，…)因此，从第1项开始的该数列为1，1，2，3，5，8，13，21，…。函数fibl和fib2分别用递归方式和迭代方式求解菲波那契数列的第n项(调用fib1、fib2时可确保参数n获得一个正整数)。【C函数代码】函数fib1和fib2存在错误，只需分别修改其中的一行代码即可改正错误。(1)函数fib1不能通过编译，请写出fib1中错误所在行修改正确后的完整代

题目

阅读以下说明和C函数代码，回答问题并将解答写在对应栏内。

【说明】

著名的菲波那契数列定义式为

f1=1 f2=1 fn=fn-1+fn-2 (n=3，4，…)

因此，从第1项开始的该数列为1，1，2，3，5，8，13，21，…。函数fibl和fib2分别用递归方式和迭代方式求解菲波那契数列的第n项(调用fib1、fib2时可确保参数n获得一个正整数)。

【C函数代码】

函数fib1和fib2存在错误，只需分别修改其中的一行代码即可改正错误。

(1)函数fib1不能通过编译，请写出fib1中错误所在行修改正确后的完整代码。

(2)函数fib2在n≤2时不能获得正确结果，请写出fib2中错误所在行修改正确后的完整代码。

相似考题

1.函数fib1、fib2求得菲波那契数列第n项(n＞40)的速度并不相同，清指出速度慢的函数名，并简要说明原因。

2.阅读下列函数说明和C函数，将应填入(n)处的字句写在对应栏内。[函数2.1说明]Fibonacci数列中头两个数均为1，从第三个数开始，每个数等于前两个数之和。下述程序计算Fibonacci数列中前15个数，并以每行5个数的格式输出。[函数2.1]include ＜stdio.h＞main(){ int i,f,f1=1,f2=1;printf("%5d%5d",f1,f2);for(i=3;i＜=15;i++){f=(1);printf("%5d",f);if((2)= =0) printf("\n");f1=12;(3);}}[函数2.2说明]函数fun(char *str1,char *str2)的功能是将字符串str2拼接到str1之后。[函数2.2]fun(char *str1,char *str2){ int i,j;for(i=0;str1[i]!='\0';i++);for(j=0;str2[j]!='\0';j++) (4);(5);}

3.试题四（共 15 分）阅读以下说明和 C 函数代码，回答问题并将解答写在答题纸的对应栏内。[说明]著名的菲波那契数列定义式为f1 = 1 f2 = 1 fn = fn-1 + fn-2 （n = 3,4,…）因此，从第 1 项开始的该数列为 1,1,2,3,5,8,13,21,…。函数 fib1 和 fib2 分别用递归方式和迭代方式求解菲波那契数列的第 n 项（调用 fib1、fib2 时可确保参数 n 获得一个正整数） 。[C函数代码][问题 1]（6 分）函数 fib1 和 fib2 存在错误，只需分别修改其中的一行代码即可改正错误。（1）函数 fib1 不能通过编译，请写出 fib1 中错误所在行修改正确后的完整代码；（2）函数 fib2 在n≤2 时不能获得正确结果，请写出 fib2 中错误所在行修改正确后的完整代码。[问题 2]（3 分）将函数 fib1 和 fib2 改正后进行测试，发现前 46 项都正确，而第 47 项的值是一个负数，请说明原因。[问题 3]（6 分）函数 fib1、fib2 求得菲波那契数列第 n 项（n>40）的速度并不相同，请指出速度慢的函数名，并简要说明原因。

4.函数fib1、fib2求得菲波那契数列第n项(n＞40)的速度并不相同，请指出速度慢的函数名，并简要说明原因。

更多“ 阅读以下说明和C函数代码，回答问题并将解答写在对应栏内。【说明】著名的菲波那契数列定义式为f1=1 f2=1 fn=fn-1+fn-2 (n=3，4，…)因此，从第1项开始的该数列为1，1，2，3，5，8，13，”相关问题

  • 第1题：

    阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】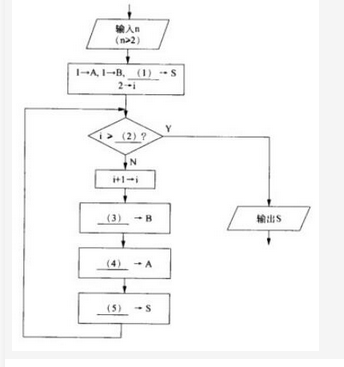


    答案：
    解析：
    （1）2或A+B（2）n（3）A+B（4）B-A（5）S+B
    【解析】

    菲波那契数列的特点是首2项都是1，从第3项开始，每一项都是前两项之和。该数列的前几项为1，1，2, 3，5，8，…。在流程图中，送初始值1—A，2—B后，显然前2项的和S应等于2,所以（1）处应填2 (或A+B)。此时2→i (i表示动态的项编号），说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和，循环可以结束了。因此（2）处填n。判断框中用“>”或“≥”的效果是一样的，因为随着i的逐步增1，只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些，以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1，继续往下计算。原来的前两项值（分别在变量A和B中）将变更成新的前两项再放到变量A和B中。

    首先可以用A+B—B实现（原A) + (原B)—(新B)，因此（3）处填A+B。为了填新A值（原来的B值)，不能用B—A，因为变量B的内容已经改变为（原A) + (原B)，而B-A正是（（原A) + (原B))-(原A)=(原B)，因此可以用B-A—A来实现新A的赋值。这样，（4）处填B-A。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以（5）处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果（这是防止逻辑上出错的好办法）。

  • 第2题：

    请编写Python程序完成以下要求： 编写函数，求斐波那契数列第n项的值，F1=1，F2=1，Fn=Fn-1+Fn-2。


    print("学Python，称为Python程序员")
    print("学Python，称为P

  • 第3题：

    斐波那契数列FN的定义为：F0=0, F1=1, FN=FN−1+FN−2, N=2, 3, …。用递归函数计算FN的空间复杂度是O（N)。


    错误

  • 第4题：

    斐波那契数列FN的定义为：F0=0, F1=1, FN=FN−1+FN−2, N=2, 3, …。用递归函数计算FN的时间复杂度是O（N!)。


    错误

  • 第5题：

    请编写Python程序完成以下要求： 编写函数，求斐波那契数列第n项的值，F0=1，F1=1，Fn=Fn-1+Fn-2。 提示：此题没有太大难度，只需要按照通项公式构造函数即可；需要注意的是：函数中需要对n=0和n=1这两种情况做特殊处理。 （得分点提示：程序的可读性、功能是否正确）


    自己验证程序的正确性

相关内容