阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：(1)以n除m并令r为所得的余数；(2)若r等于0，算法结束；n即为所求；(3)将n和r分别赋给m和n，返回步骤(1)。[流程图][问题1] 将流程图中的(1)～(4)处补充完整。[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。

题目

阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。

[说明]

下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：

(1)以n除m并令r为所得的余数；

(2)若r等于0，算法结束；n即为所求；

(3)将n和r分别赋给m和n，返回步骤(1)。

[流程图]

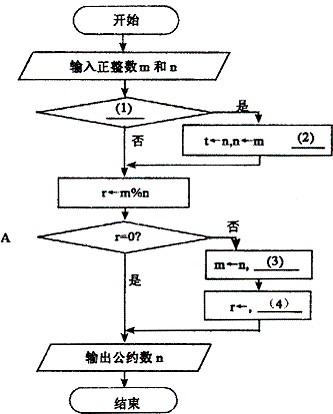
[问题1] 将流程图中的(1)～(4)处补充完整。

[问题2] 若输入的m和n分别为27和21，则A中循环体被执行的次数是(5)。

相似考题

1.阅读下列说明和流程图，将应填入(n)处的语句写在对应栏内。【说明】下列流程图用于从数组K中找出一切满足：K(I)+K(J)=M的元素对(K(I)，K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列，M是给定的常数。【流程图】此流程图1中，比较“K(I)+K(J):M”最少执行次数约为(5)。

2.阅读以下说明和流程图，回答问题1～2，将解答填入对应的解答栏内。[说明]下面的流程图描述了计算自然数1到N(N≥1)之和的过程。[流程图][问题1] 将流程图中的(1)～(3)处补充完整。[问题2] 为使流程图能计算并输出1*3+2*4+…+N*(N+2)的值，A框内应填写(4)；为使流程图能计算并输出不大于N的全体奇数之和，B框内应填写(5)。

3.阅读以下说明，回答问题，将解答填入对应的解答栏内。. [说明] 请完成流程图以描述在数据A(1)至A(10)中求最大数和次大数的程序的算法。并将此改成PAD图。该算法的流程图如下图：

4.阅读以下说明，回答问题，将解答填入对应的解答栏内。[说明] 将一个正整数分解质因数。例如：输入90，打印出90=2*3*3*5。main ( ){int n, i;printf ( "\n please input a number: \n");scanf ( "% d" ,&u);printf ( "%d =" ,n);for((1)){while((2)){if((3)){ printf ("%d*",i);(4)}elsebreak;}}printf (“%d”，n)；}

更多“ 阅读以下说明和流程图，回答问题1-2，将解答填入对应的解答栏内。[说明]下面的流程图采用欧几里得算法，实现了计算两正整数最大公约数的功能。给定正整数m和 n，假定m大于等于n，算法的主要步骤为：(1)以n除m并令”相关问题

  • 第1题：

    阅读以下说明和流程图，回答问题，并将解答填入对应栏内。

    【说明】

    求解约瑟夫环问题。算法分析：n个士兵围成一圈，给他们依次编号，班长指定从第w个士兵开始报数，报到第s个士兵出列，依次重复下去，直至所有士兵都出列。

    【流程图】

    【问题】

    将流程图中的(1)～(5)处补充完整。


    正确答案：(1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count
    (1)L[i].nextp=1 (2) k=w-1 (3) count!=n (4) ++I (5) ++count

  • 第2题：

    试题（15 分）阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏 内。【说明】设有整数数组 A[1：N]（N>1），其元素有正有负。下面的流程图在该数组 中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标 K、元素 个数 L 以及最大的和值 M。例如，若数组元素依次为 3，-6，2，4，-2，3，-1，则输出 K=3，L=4,M=7。 该流程图中考察了 A[1：N]中所有从下标 i 到下标 j（j≥i）的各元素之和 S，并动态地记录其最大值 M。【流程图】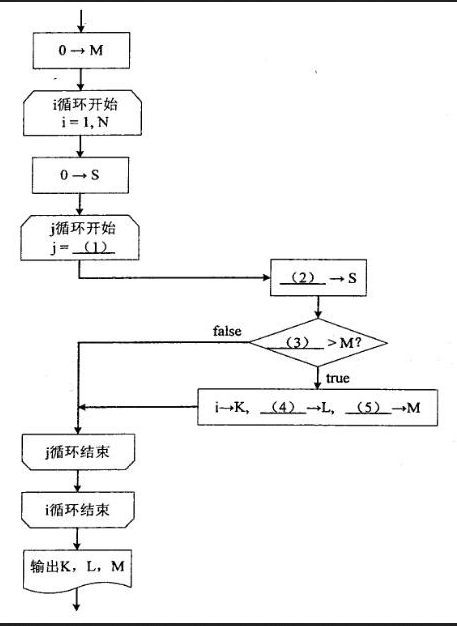

    注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为 1，格式为：循环控制变量=初值，终值


    答案：
    解析：
    1、j=i+1
    2、S+A[j]
    3、S
    4、j-i+1
    5、S

  • 第3题：

    阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
    【说明】
    设有整数数组A[1：N]（N>1），其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标K、元素个数L以及最大的和值M。
    例如，若数组元素依次为3，-6，2，4，-2，3，-1，则输出K=3，L=4,M=7。该流程图中考察了A[1：N]中所有从下标i到下标j（j≥i）的各元素之和S，并动态地记录其最大值M。

    【流程图】



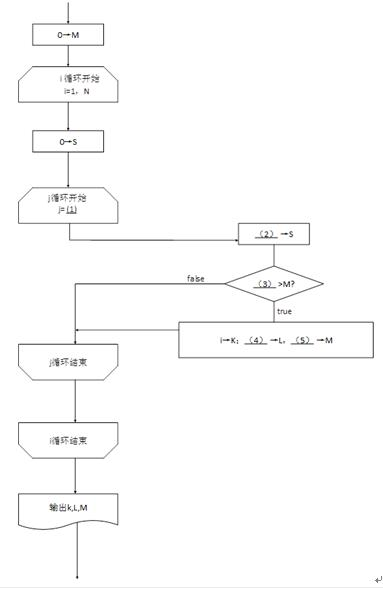
    注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1，格式为：循环控制变量=初值，终值


    答案：
    解析：
    （1）（1）i，N
    （2）S+A[j]
    （3）S
    （4）j-i+1
    （5）S
    【解析】
    要想在数组中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标K、元素个数L以及最大的和值M
    那么，会将数组从第一个元素出发，依次比较A[1]，A[1] +A[2]，A[1] +A[2]+A[3]，……，A[1] +A[2]+…+A[N]，然后再比较A[2], A[2] +A[3]，A[2] +A[3]+A[4]，……，A[2] +A[3]+…+A[N]，然后再比较A[3] +A[4]，A[3] +A[4]+A[5]，……，A[3] +A[4]+…+A[N]，直到最后一个元素A[N]。按照这种逻辑，要使用两个循环，且要保存之前求和项。一个是i循环，从1到N递增，另一个是j循环，j表示的是求和项的最大下标值，那么j从i开始，且要小于N。 S+A[j]->S不断保留A[i]+ A[i+1]+…A[j]的值，直到j循环结束。并将S的值与之前保存的M的值进行比较，如果S>M，则将S的值赋给M，并求出L值，在这里，i是最小下标值，j是最大下标值，那么L=j-i+1。如果S

  • 第4题：

    阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。 【说明】 设有整数数组A[1：N]（N>1），其元素有正有负。下面的流程图在该数组中寻找连续排列的若干个元素，使其和达到最大值，并输出其起始下标K、元素个数L以及最大的和值M。 例如，若数组元素依次为3，-6，2，4，-2，3，-1，则输出K=3，L=4,M=7。该流程图中考察了A[1：N]中所有从下标i到下标j（j≥i）的各元素之和S，并动态地记录其最大值M。

    【流程图】注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1，格式为：循环控制变量=初值，终值


    正确答案：（1）i，N
    （2）S+A[j]
    （3）S
    （4）j-i+1
    （5）S

  • 第5题：

    第一题 阅读以下说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。
    【说明】
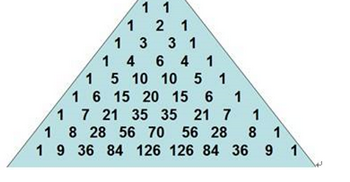
    对于大于1的正整数n，(x+1)n可展开为

    问题：1.1 【流程图】

    注：循环开始框内应给出循环控制变量的初值和终值，默认递增值为1。
    格式为：循环控制变量=初值，终值，递增值。


    答案：
    解析：
    （1）2，n，1
    （2）A[k]
    （3）k-1，1，-1
    （4）A[i]+A[i-1]
    （5）A[i]
    【解析】

    （1）（3）空为填写循环初值终值和递增值，题目中给出的格式为循环控制变量=初值，终值，递增值。按照题意，实质为求杨辉三角。如下图：

相关内容