计算机中16位浮点数的表示格式如图1所示：某机器码为1110001010000000。若阶码为移码且尾数为反码，其十进制真值为(8)；若阶码为移码且尾数为原码，其十进制真值为(9)；若阶码为补码且尾数为反码，其十进制真值为(10)；若阶码为补码且尾数为原码，其十进制真值为(11)，将其规格化后的机器码为(12)。A．0.078125B．1.45C．20D．20.697395

题目

计算机中16位浮点数的表示格式如图1所示：

某机器码为1110001010000000。

若阶码为移码且尾数为反码，其十进制真值为(8)；

若阶码为移码且尾数为原码，其十进制真值为(9)；

若阶码为补码且尾数为反码，其十进制真值为(10)；

若阶码为补码且尾数为原码，其十进制真值为(11)，将其规格化后的机器码为(12)。

A．0.078125

B．1.45

C．20

D．20.697395

相似考题

1.设机器中浮点数的格式如下：其中阶码6位，包括1位符号位，尾数10位(含1位数符)，浮点数的基为2。阶码用补码表示，尾数用原码表示。对于十进制数-25.8375，当阶码用补码表示、尾数用原码表示时，得到的规格化机器码为(38)；当阶码用移码表示、尾数用原码表示时，得到的规格化机器码为(39)；当阶码用原码表示，尾数用补码表示时，得到的规格化机器码为(40)。A．1001011100111000B．1110101100111010C．1001011000111010D．1001011100111010

2.某计算机系统中，16位浮点数的表示格式如图6-1所示。其中阶码4位(含1位符号)为定点整数，尾数12位(含1位符号)为定点小数，设一个数机器码为1110001010000000。若阶码为移码且尾数为原码，则其十进制数真值为(2)；若阶码为补码且尾数为补码，则其十进制数真值规格化后的机器码为(3)。A．20B．25C．0.078125D．20.969375

3.下面是机器中浮点数的表示格式：设浮点数的基为2。若阶码用补码表示、尾数用原码表示，十进制数-51.875采用上述格式可表示为(7)；若阶码用移码表示、尾数用补码表示，该数可表示为(8)。A．0110 111001111100B．0110 011001111100C．0110 001110011111D．0101 011001111100

4.计算机中十六位浮点数的表示格式为某机器码为1110001010000000，若阶码为移码且尾数为反码，则其十进制真值为(7)；若阶码为移码且尾数为原码，则其十进制真值为(8)；若阶码为补码且尾数为反码，则其十进制真值为(9)；若阶码为补码且尾数为原码．则其十进制真值为(10)，将其规格化后的机器码为(11)。A．0.078125B．20C．20.969375D．1.25

参考答案和解析
正确答案：C
解析：本题考查计算机数据的编码，涉及原码、补码、反码和移码以及浮点数规格化处理。同一个数可以有不同的浮点表示形式，阶码的大小可以用来调节数值中小数点的位置。将数值数据表示成N=M+RE，M被称为N的尾数，E是N的指数或称阶码，而只是该阶码的基数。题中阶码用4位二进制整数1110表示，尾数用12位二进制小数001010000000表示，尾数中含有符号位，其最高位即符号位为0。下面具体解答各个问题。(8)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：[X]移码=23+X=(1110)2=(14)10，可此求得阶码真值为6。如果尾数为反码，从符号为可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-2+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125+26=20。(9)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值位0.3125。这样该机器码的真值也是20。(10)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义[X]补码=24+x=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同问题(8)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(11)如果阶码是补码，尾数是原码，可分别参照问题(10)和问题(9)求出阶码和尾数的真值分别为-2和0.3125这样该机器码的真值也是0.078125。(12)这是对浮点数进行规格化处理。规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1xxx…xx(x为0或1)。对于不符合这一规定的浮点数。可采用改变阶码的大小并同时左右移尾数的方法来满足这一规定。显然尾数0.01010000000不符合要求，应左移1位，而阶码则相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。
更多“ 计算机中16位浮点数的表示格式如图1所示：某机器码为1110001010000000。若阶码为移码且尾数为反码，其十进制真值为(8)；若阶码为移码且尾数为原码，其十进制真值为(9)；若阶码为补码且尾数为反码，其十”相关问题

  • 第1题：

    ●计算机中十六位浮点数的表示格式为

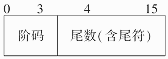
    某机器码为1110001010000000，

    若阶码为移码且尾数为反码，则其十进制真值为 (7) ；

    若阶码为移码且尾数为原码，则其十进制真值为 (8) ；

    若阶码为补码且尾数为反码，则其十进制真值为 (9) ；

    若阶码为补码且尾数为原码，则其十进制真值为 (10) ，将其规格化后的机器码为 (11) 。

    (7)～(10) A．0.078125

    B．20

    C．20.969375

    D．1.25

    (11) A．11110101000000

    B．1110001010000000

    C．1101010100000000

    D．11110001010000


    正确答案：B,B,A,A,C
    【解析】(7)如果阶码为移码，由于阶码是4位二进制整数，设真值为X，根据整数移码定义：［X］移码=23+X(1110)2=(14)10，可求得阶码真值为6。如果尾数为反码，从符号位可判断尾数是正数，根据小数反码定义，正小数的反码就是其自身，可求得尾数的真值为：(0.01010000000)2=(2-2+2-4)=(0.3125)10，根据浮点数定义，该机器码真值为0.3125*26=20。(8)如果阶码为移码，同上，真值为6。如果尾数是原码，从符号位可判断尾数是正数，根据小数原码定义，正小数的原码就是其本身，可求得尾数的真值为0.3125。由此可知该机器码真值也是20。(9)如果阶码为补码，由于阶码是4位二进制整数，从符号位判断为负数，设真值为X，根据负整数定义［X］补码=24+X=(1110)2=(14)10，求得阶码的真值为-2。如果尾数为反码，同(7)一样求出尾数的真值为0.3125。这样，该机器码真值为0.3125*2-2=0.078125。(10)如果阶码是补码，尾数是原码，求出阶码和尾数的真值分别为-2和0.3125，这样该机器码的真值也是0.078125。(11)对浮点数进行规格化处理，规定浮点数的尾数部分用纯小数形式表示，当尾数的值不为0时，其绝对值应大于或等于0.5，用二进制表示为0.1XXX…XX(X为0或1)。对于不符合这一规定的浮点数，可改变阶码的大小并同时用左右移尾数的方法来满足这一规定。显然尾数0.01010000000不合要求，应左移1位，而阶码则应相应地减1，因此规格化处理后的阶码为1101，尾数为010100000000。

  • 第2题：

    计算机中十六位浮点数的表示格式为图1.4

    某机器码为1010001010000000。

    若阶码为移码且尾数为反码，则其真值为(60)；

    若阶码为移码且尾数为原码，则其真值为(61)；

    若阶码为补码且尾数为反码，则其真值为(62)；

    若阶码为补码且尾数为原码，则其真值为(63)，将其规格化后的机器码为(64)。

    A．0.00000001012

    B．2010

    C．1.2510

    D．20.96937510


    正确答案：C

  • 第3题：

    设浮点数格式为：阶码5位（含1位阶符），尾数11位（含1位数符）。写出51/128、-27/1024、7.375、-86.5所对应的机器数。要求如下： （1）阶码和尾数均为原码。 （2）阶码和尾数均为补码。 （3）阶码为移码，尾数为补码。


    x=49/128=0.011 0001B y = -27 =-1 1011B化成规格化数: x=0.11 0001 0000*2^(-1) y=-0.11 0110 0000*2^(+101)(1) 阶码和尾数均为原码 [ x ] = 1 0001 ； 0.11 0001 0000 [ y ] = 0 0101 ； 1.11 0110 0000(2)阶码和尾数均为反码 [ x ] = 1 1110 ； 0.11 0001 0000 [ y ] = 0 0101 ； 1.00 1001 1111(3) 阶码和尾数均为补码 [ x ] = 1 1111 ； 0.11 0001 0000 [ y ] = 0 0101 ； 1.00 1010 0000(4)阶码为移码，尾数为补码 [ x ] = 0 1111 ； 0.11 0001 0000 [ y ] = 1 0101 ； 1.00 1010 0000

  • 第4题：

    某计算机系统中，16位浮点数的表示格式如图6-1所示。其中，阶码4位(含1位符号)为定点整数，尾数12位(含1位符号)为定点小数。

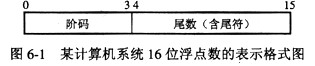
    设一个数机器码为1110001010000000，若阶码为移码且尾数为原码，则其十进制数真值为(1)。

    A．20

    B．25

    C．0.078125

    D．20.969375


    正确答案：A
    解析：为了充分利用尾数来表示更多的有效数字，即提高数据的表示精度，通常采用规格化浮点数。规定化浮点数在运算结束将运算结果存到计算机中时，必须是规格化的浮点数。规格化浮点数尾数的最高数值位是有效数字，即正尾数0.5≤F1，负尾数-1F≤-0.5。要求规格化以后，其尾数部分是正数时为0.1×××的形式，是负数时，对于原码为1.1×××的形式，对于补码为1.0×××的形式，可以通过尾数小数点的左右移动和阶码的变化实现。对于本试题的解答思路是，对给定的机器码按给定的浮点数格式得到阶码和尾数，然后将阶码变为十进制数，最后得到浮点数的十进制真值。判断如果给定的浮点数机器码不是规格化表示的，则可将其表示为规格化的机器码。规格化时，先看给定的浮点数机器码的尾数是用什么码表示的，然后看看是否已是规格化数，如不是，将尾数小数点移位，但要注意，为保持浮点数的真值不变，阶码一定要相应地调整。另外在解答此类题目时，还要注意题目条件中给出的阶码和尾数是用什么码表示的，否则很容易出错，而得不到正确的计算结果。针对本道题目，对所给机器码1110001010000000，按所规定的浮点数表示形式，可知阶码为1110(最高位为阶符1)，尾数为001010000000(最高位为尾符0)。①若阶码为移码，1110表示为十进制数加6，尾数为原码表示加0.010lB，所以浮点数为26×0.0101B=010100B=20。②若阶码为补码，1110表示为十进制数减2；尾数为补码，因该尾数为正数，即加0.0101，该浮点数为2-2×0.0101B=0.000101B=0.078125D。将此浮点数用规格化数形式表示：2-2÷0.0101B=2-3×0.101B，阶码-3的补码为1101，因为浮点数规格化要求尾数最高数据位为有效数据位，即尾数绝对值大于等于0.5。实际判断中，对于尾数以补码表示时，看符号位与最高位是否相同，如不相同即为规格化数，如相同即为非规格化数，故规格化后的机器码为1101010100000000。对本题所给出的机器码来说，就是使其尾数001010000000左移一位成为010100000000，相当于尾数数值乘2，相应地其阶码就应减1，即-2减1得-3。

  • 第5题：

    下面是某种计算机的32位短浮点数格式如图1.7

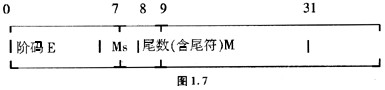
    其中，M为用定点小数表示的尾数的绝对值，占23位；Ms是尾数的符号位，占1位；Ms和M一起表示尾数。E为用定点整数表示的阶码，占8位。若机器表示中取阶码的基数为2，求采用下列五种不同编码方式时，浮点数-123625E-3(隐含基数为10)规格化后的机器码：

    阶码用补码方式、尾数用原码方式时，为(80)；

    阶码用补码方式、尾数用反码方式时，为(81)；

    阶码用移码方式、尾数用原码方式时，为(82)；

    阶码用移码方式、尾数用补码方式时，为(83)；

    阶码用移码方式、尾数用反码方式时，为(84)；

    A．10000111100001000110000000000000

    B．00000111100001000101111111111111

    C．10000111111110000101111111111111

    D．00000111111110111010000000000000


    正确答案：D

相关内容