某高可靠性计算机系统由图2-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度只为(4)。A．0.9999B．0.9975C．0.9475D．0.8574
题目
某高可靠性计算机系统由图2-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度只为(4)。
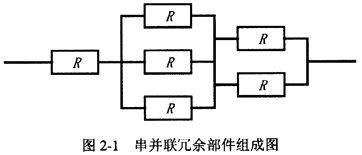
A．0.9999
B．0.9975
C．0.9475
D．0.8574
相似考题
更多“ 某高可靠性计算机系统由图2-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度只为(4)。A．0.9999B．0.9975C．0.9475D．0.8574 ”相关问题
-
第1题：
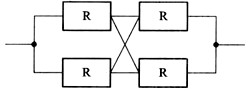
某计算机系统由图5-35所示的部件构成，假定每个部件的千小时可靠度R均为0.9，则该系统的千小时可靠度约为______。
A．0.9801
B．0.951
C．0.9
D．0.99
正确答案：A
解析：不要被两并联子系统之间的网状连线所误导，其实可以将这些网状连线“拧成”一根两头分叉的导线来看待，其等价结构图如图5-37所示。两个R并联的可靠度为：1-(1-0.9)2=0.99。我们可以将两个并联的R部件看成一个部件R1，R1的可靠度为0.99，所以该系统的可靠度为：0.99×0.99=0.9801。所以答案为A。 -
第2题：
某高可靠性计算机系统由下图所示的冗余部件构成。若每个部件的千小时可靠度 R均为0.9，则该计算机系统的千小时可靠度为(18)；该计算机系统的失效率丸可使用(19)来计算。注：t表示时间。
A．0.656
B．0.729
C．0.801
D．0.864
正确答案：C
解析：从可靠性角度分析，该计算机系统是一个并串联系统，其中有三个部件并联冗余构成一个功能部件，其可靠度为0.999；两个可靠度为0.9的部件并联冗余，其可靠度为0.99。这两个并联冗余的部件再与可靠度为0.9的两个部件串联构成该计算机系统，故该计算机系统的可靠度为；
Rs=0.9×0.999×0.99×0.9=0.801
根据可靠度的定义：R(t)＝e-λt，失效率入可以用式-InR/t来进行计算。 -
第3题：
某高可靠性计算机系统由图6-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度R为（ ）。
A.0.9999
B.0.9975
C.0.9475
D.0.8574答案：C解析：系统可靠性计算，这是串并联混合系统，每个R可靠性是0.95，总可靠性是 0.95*（1-（1-0.95）^3）（1-（1-0.95）^2）=0.9475.本题计算有个小技巧，这种复杂的计算先不要硬算，看下相乘的结果，肯定是小于0.95的，也不能太离谱。
-
第4题：
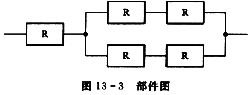
某计算机系统由图13-3所示的部件构成，假定每个部件的千小时可靠度R均为0.9，则该系统的千小时可靠度约为(36)。
A．0.882
B．0.951
C．0.9
D．0.99
正确答案：A
解析：要被两并联子系统之间的网状连线所误导，其实可以将这些网状连线“拧成”一根两头分叉的导线来看待，其等价结构图如图13-31所示。两个R并联的可靠度为：1-(1-0.9)2=0.99。我们可以将两个并联的R部件看成一个部件R1，R1的可靠度为0.99，所以该系统的可靠度为：0.9×0.99×0.99=0.88209。 -
第5题：
某系统由下图所示的冗余部件构成。若每个部件的千小时可靠度都为R，则该系统的千小时可靠度为( )。
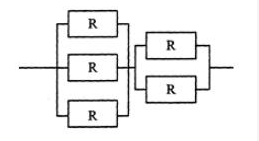
答案：B解析：本题考查系统可靠性。计算机系统是一个复杂的系统，而且影响其可靠性的因素也非常繁复，很难直接对其进行可靠性分析。若采用串联方式，则系统可靠性为每个部件的乘积R=R1×R2×R3×…×Rn；若采用并联方式，则系统的可靠性为R=1-（1-R1）×（1-R2）×（1-R3）×…×（1-Rn）。在本题中，既有并联又有串联，计算时首先我们要分别计算图中两个并联后的可靠度，它们分别为（1-（1-R）3）和（1-（1-R）2）。，然后是两者串联，根据串联的计算公式，可得系统的可靠度为（1-（1-R）3）（1-（1-R）2）。