阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。【流程图】
题目
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。
【说明】
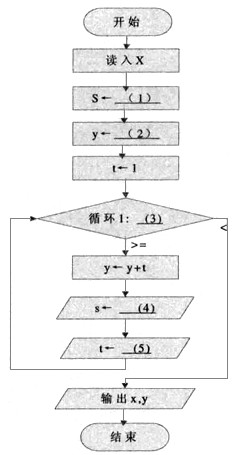
下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差要求。
【流程图】
相似考题
更多“ 阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。【说明】下列流程图用泰勒(Taylor)展开式y=ex=1+x+x2/2!+x3/3!+…+xn/n!+…计算并打印ex的近似值,其中用ε(>0)表示误差”相关问题
-
第1题:
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。
【说明】
有数组A(4,4),把1到16个整数分别按顺序放入A(1,1),…,A(1,4),A(2,1),…,A(2,4),A(3,1),…,A(3,4),A(4,1),…,A(4,4)中,下面的流程图用来获取数据并求出两条对角线元素之积。
【流程图】
 正确答案:(1)141 (2)141 (3)1 (4)s×A[ii] (5)s×A[5-ii]
正确答案:(1)141 (2)141 (3)1 (4)s×A[ii] (5)s×A[5-ii]
(1)1,4,1 (2)1,4,1 (3)1 (4)s×A[i,i] (5)s×A[5-i,i] 解析:本题考查用程序流程图描述数组及求对角线的和。
题目要求把1到16个整数分别按顺序放入A(1,1),…,A(1,4),A(2,1),…,A(2,4), A(3,1),…,A(3,4),A(4,1),…,A(4,4)中,那么数组中的元素刚好构成一个方阵,用流程图求出这个方阵的对角线之积。下面来具体分析流程图。
第(1)空与第(2)空应该结合起来完成,它们都是一个循环判断语句的条件,从图中可以看出,如果这两个条件都成立,则读出当前数组中的元素值,根据题目要求,数组中的元素个数是每行4个每列4个,那么循环的上界应该是4,而下标是从1开始的,因此这两个空答案为1,4,1。
第(3)空是一个赋值语句,给变量s赋一个初值,从图中后面的语句不难看出s中存放的是求积的结果,那么在求积以前,s的值应该为1,因此此空答案为1。
第(4)空也是一个赋值语句,是在循环条件判断语句下,我们已经知道变量s中存放的是每次求积的结果,那么此空很明显是用来求积的,用当前取到的对角线元素乘以变量s中存放的值,因此此空答案为s×A[i,i]。
第(5)空和上一空非常相似,但它是用来求另外一条对角线的积的,它也是在一个循环下来实现的,这条对角线的元素位置与上面那条具有对称的特点,因此此空答案为s×A[5-i,i]。 -
第2题:
阅读下列说明和流程图,将应填入(n)处的语句写在对应栏内。
【说明】
设学生(学生数少于50人)某次考试的成绩按学号顺序逐行存放于某文件中,文件以单行句点“.”为结束符。下面的流程图用于读取该文件,并把全部成绩从高到低排序到数组B[50]中。
【流程图】
 正确答案:(1)B[0]←a (2)i←0 (3)a="." (4)aB[j] (5)j--
正确答案:(1)B[0]←a (2)i←0 (3)a="." (4)aB[j] (5)j--
(1)B[0]←a (2)i←0 (3)a="." (4)aB[j] (5)j-- 解析:本题考查用程序流程图来描述排序。
题目要求将文件中学生的成绩读出,并把全部成绩从高到低排序到数组B[50]中。这里面涉及两个问题,第一是从文件中读数,文件中的数据是以单行句点“.”为结束符的,在未读到此符号前,应该将继续取数据。第二是排序,每取到一个学生的成绩都要与数组的学生成绩比较,按照从高到低的顺序在数组中找到合适的位置存放。下面来具体分析流程图。
第(1)空在条件判断为假的情况下执行流程中,如果条件为假说明从文件中取到的数据是学生成绩。从程序流程图中可以看到,从文件中读的数据存放在变量a中,而此空是第一次取数据,应该存放数组B的第一个位置,因此此空答案为B[0]←a。
第(2)空是紧接着第(1)空来的,在上面已经把从文件中读到的第一个数存放到了数组中,接下来应该处理数组的下标问题,从后面的流程中可以推断出变量i是存放数组当前下标的,而且没有初值,那么此空的任务应该是用来给变量i赋一个初值,而对数组的操作应该从头开始,因此此空答案为i←0。
第(3)空是循环的判断条件,如果条件成立则结束,在这之前又对文件进行了一次读数,根据我们上面的分析只有在读到了结束符时程序才结束,那么此空肯定是判断从文件中读到的数据是否为结束符,因此此空答案为a="."?。
第(4)空也是一个循环的判断条件,如果条件成立,则将取到的数存放到数组的当前下标位置;如果不成立,则循环找到合适的位置再存放。从这里我们不难推断出,流程图中是将从文件取到的成绩与当前数组中的最小成绩进行比较的,而当前数组中的最小成绩存放在位置j中,因此此空答案为aB[i]?。
第(5)空在循环体中,这个循环的作用是为当前从文件中读到的成绩在已经排好序的数组元素中找到合适的位置,找到了就要插入,数组中的元素是按从大到小排列的,在查找合适位置时是从后往前依次比较,因此此空的任务应该是将数组的下标往前移动,所以此空答案为“i--”。 -
第3题:
●试题一
阅读下列说明和流程图,将应填入(n)处的语句写在答题纸的对应栏内。
【说明】
下列流程图用于从数组K中找出一切满足:K(I)+K(J)=M的元素对(K(I),K(J))(1≤I≤J≤N)。假定数组K中的N个不同的整数已按从小到大的顺序排列,M是给定的常数。
【流程图】
此流程图1中,比较"K(I)+K(J)∶M"最少执行次数约为 (5) 。

图1
正确答案:
●试题一【答案】(1)(2)<(3)I+l->I(4)J-1->J(5)「N/2」【解析】该算法的思路是:设置了两个变量I和J,初始时分别指向数组K的第一个元素和最后一个元素。如果这两个元素之和等于M时,输出结果,并这两个指针都向中间移动;如果小于M,则将指针I向中间移动(因为数组K已按从小到大的顺序排列);如果大于M,则将指针J向中间移动(因为数组K已按从小到大的顺序排列)。当IJ时,说明所有的元素都搜索完毕,退出循环。根据上面的分析,(1)、(2)空要求填写循环结束条件,显然,(1)空处应填写"",(2)空处应填写"<"。这里主要要注意I=J的情况,当I=J时,说明指两个指针指向同一元素,应当退出循环。(3)空在流程图有两处,一处是当K(I)+K(J)=M时,另一处是当K(I)+K(J)<M时,根据上面分析这两种情况都要将指针I向中间移动,即"I+1->I"。同样的道理,(4)空处应填写"J-1->J"。比较"K(I)+K(J):M"最少执行次数发生在第1元素与第N个元素之和等于M、第2元素与第N-1个元素之和等于M、……,这样每次比较,两种指针都向中间移动,因此最小执行次数约为"N-2"。 -
第4题:
阅读以下说明和流程图,将应填入(n)处的字句写在对应栏内。
[说明]
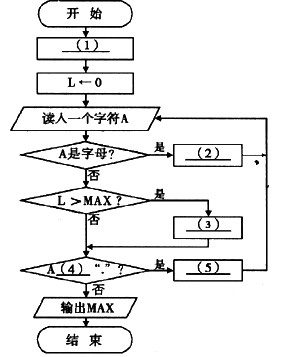
下面的流程图用于计算一个英文句子中最长单词的长度(即单词中字母个数)MAX。假设该英文句子中只含字母、空格和句点“.”,其中句点表示结尾,空格之间连续的字母串称为单词。
[流程图]
 正确答案:(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0
正确答案:(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0
(1)MAX←0 (2)←L+1 (3)MAX←L (4)≠ (5)L←0 解析:本题用到的三个变量及其作用分别为:A,存放输入的一个字符;MAX,存放当前为止最长单词的长度;L,存放当前单同的长度。
(1)使用变量MAX应先赋予初值,由上下文知其初值为0;
(2)读取当前单词时,每读人一个字母,单词长度值L应增1;
(3)当前单词长度L比MAX时,应更新MAX的值;
(4)若当前字符不是句点,应当继续读取字符;
(5)读取下一个单词前,应当重置L的值。 -
第5题:
●试题一
阅读下列说明和流程图,将应填入(n)的字句写在答题纸的对应栏内。
【说明】
下列流程图(如图4所示)用泰勒(Taylor)展开式
sinx=x-x3/3!+x5/5!-x7/7!+…+(-1)n×x 2n+1/(2n+1)!+…
【流程图】
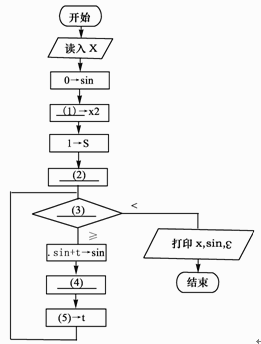
图4
计算并打印sinx的近似值。其中用ε(>0)表示误差要求。
正确答案:
●试题一【答案】(1)x*x(2)x->t(3)|t|∶ε(4)s+2->s(5)(-1)*t*x2/(s*(s-1))【解析】该题的关键是搞清楚几个变量的含义。很显然变量t是用来保存多项式各项的值,变量s和变量x2的作用是什么呢?从流程图的功能上看,需要计算1!、3!、5!,……,又从变量s的初值置为1可知,变量s主要用来计算这此数的阶乘的,但没有其他变量用于整数自增,这样就以判断s用来存储奇数的,即s值依次为1、3、5,……。但x2的功能还不明确,现在可以不用管它。(2)空的作用是给t赋初值,即给它多项式的第一项,因此应填写"x->t"。(3)空处需填写循环条件,显然当t的绝对值小于ε(>0)就表示已经达到误差要求,因此(3)空应填入"|t|∶ε"。由变量s的功能可知,(4)空应当实现变量s的增加,因此(4)空应填入"s+2->s"。(5)空应当是求多项式下一项的值,根据多项式连续两项的关系可知,当前一项为t时,后一项的值为(-1)*t*x*x/(s*(s-1))。但这样的话,每次循环都需要计算一次x*x,计算效率受到影响,联想到变量x2还没用,这时就可以判断x2就是用来存储x*x的值,使得每次循环者少进行一次乘法运算。因此(1)空处应填入"x*x",(5)空处应填入"(-1)*t*x2/(s*(s-1))"。
