若在9阶B-树中插入关键字引起结点分裂，则该结点在插入前含有的关键字个数为(29)。A．4B．5C．8D．9

阅读下列说明、图和C代码。

[说明5-1]

B树是一种多叉平衡查找树。一棵m阶的B树，或为空树，或为满足下列特性的m叉树：

①树中每个结点最多有m棵子树；

②若根结点不是叶子结点，则它至少有两棵子树；

⑧除根之外的所有非叶子结点至少有[m/2]棵子树；

④所有的非叶子结点中包含下列数据信息：

(n，A0，K1，A1，K2，A2， …，Kn，An)其中：Ki(i=1，2，…，n)为关键字，且Ki＜Ki+1(i=1，2，…，n-1)；Ai(i=0，1，…，n)为指向子树根结点的指针，且指针Ai-1，所指子树中所有结点的关键字均小于Ki，Ai+1，所指子树中所有结点的关键字均大于Ki，n为结点中关键字的数目。

⑤所有的叶子结点都出现在同一层次上，并且不带信息(可以看作是外部结点或查找失败的结点，实际上这些结点不存在，指向这些结点的指针为空)。

例如，一棵4阶B树如下图所示(结点中关键字的数目省略)。

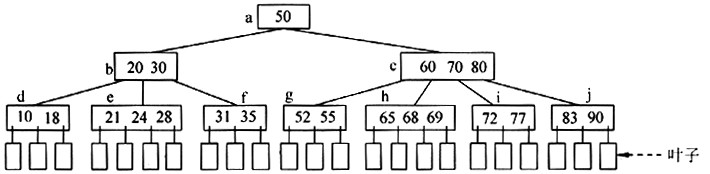
B树的阶M、bool类型、关键字类型及B树结点的定义如下：

define M 4 /*B树的阶*/

typedef enum {FALSE=0,TRUE=1}bool；

typedef int ElemKeyType；

typedef struct BTreeNode {

int numkeys； /*结点中关键字的数日*/

struct BTreeNode*parent； /*指向父结点的指针，树根的父结点指针为空*/

struct BTreeNode *A[M]； /*指向子树结点的指针数组*/

ElemKeyType K[M]； /*存储关键字的数组，K[0]闲置不用*/

}BTreeNode；

函数SearchBtree(BTreeNode*root，ElemKcyTypeakey,BTreeNode：*pb)的功能是：在给定的一棵M阶B树中查找关键字akey所在结点，若找到则返回TRUE，否则返回 FALSE。其中，root是指向该M阶B树根结点的指针，参数ptr返回akey所在结点的指针，若akey不在该B树中，则ptr返回查找失败时空指针所在结点的指针。例如，在上图所示的4阶B树中查找关键字25时，ptr返回指向结点e的指针。

注；在结点中查找关键字akey时采用二分法。

[函数5-1]

bool SearchBtree(BTreeNode* root, ElemKeyType akey, BTreeNode **ptr)

{

int lw, hi, mid;

BTreeNode*p = root;

*ptr = NULL;

while ( p ) {

1w = 1; hi=(1);

while (1w ＜= hi) {

mid = (1w + hi)/2;

if (p -＞ K[mid] == akey) {

*ptr = p;

return TRUE;

}

else

if ((2))

hi=mid - 1;

else

1w = mid + 1;

}

*ptr = p;

p = (3);

}

return FALSE;

}

[说明5-2]

在M阶B树中插入一个关键字时，首先在最接近外部结点的某个非叶子结点中增加一个关键字，若该结点中关键字的个数不超过M-1，则完成插入；否则，要进行结点的“分裂”处理。所谓“分裂”，就是把结点中处于中间位置上的关键字取出来并插入其父结点中，然后以该关键字为分界线，把原结点分成两个结点。“分裂”过程可能会一直持续到树根，若树根结点也需要分裂，则整棵树的高度增加1。

例如，在上图所示的B树中插入关键字25时，需将其插入结点e中。由于e中已经有3个关键字，因此将关键字24插入结点e的父结点b，并以24为分界线将结点e分裂为e1和e2两个结点，结果如下图所示。

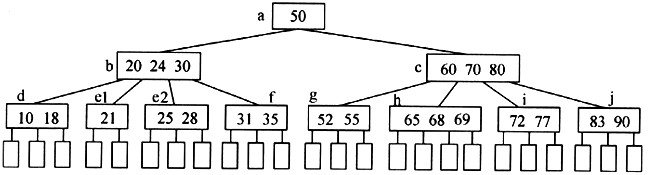
函数Isgrowing(BTreeNode*root，ElemKeyTypeakey)的功能是：判断在给定的M阶B树中插入关键字akey后，该B树的高度是否增加，若增加则返回TRUE，否则返回FALSE。其中，root是指向该M阶B树根结点的指针。

在函数Isgrwing中，首先调用函数SearchBtree(即函数5-1)查找关键字akey是否在给定的M阶B树中，若在，则返回FALSE(表明无需插入关键字akey，树的高度不会增加)；否则，通过判断结点中关键字的数目考查插入关键字akey后该B树的高度是否增加。

[函数5-2]

bool Isgrowing(BTreeNode* root, ElernKeyType akey)

{ BTreeNode *t, *f;

if( !SearchBtree((4) )