阅读以下说明和流程图，回答问题将解答填入对应栏。[说明]本流程图实现采用递归函数来求一个整数数组中从元素0到元素n中的最小值。该算法思想是这样的，首先我们假设有一个求数组中最小元素的函数，然后，在求某一具有n的元素的数组的最小值时，只要求将前n-1的元素的最小值与第n个元素比较即可。不断地重复这一过程，直到数组中只剩下一个元素，那么它必定是最小值。注：int min(int X,int y)为返回两数中最小数的函数。int minInArray(int a[],int n)为返回数组中最小数的函数。min

题目

阅读以下说明和流程图，回答问题将解答填入对应栏。

[说明]

本流程图实现采用递归函数来求一个整数数组中从元素0到元素n中的最小值。该算法思想是这样的，首先我们假设有一个求数组中最小元素的函数，然后，在求某一具有n的元素的数组的最小值时，只要求将前n-1的元素的最小值与第n个元素比较即可。不断地重复这一过程，直到数组中只剩下一个元素，那么它必定是最小值。

注：int min(int X,int y)为返回两数中最小数的函数。

int minInArray(int a[],int n)为返回数组中最小数的函数。

minA为数组中最小值。

[问题l]

将流程图的(1)～(4)处补充完整。

[问题2]

min()函数的定义为(5)。

相似考题

1.阅读以下说明和流程图，填补流程图中的空缺(1)～(9)，将解答填入对应栏内。【说明】假设数组A中的各元素A(1)，A(2)，…，A(M)已经按从小到大排序(M≥1)；数组B中的各元素B(1)，B(2)，…，B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后，可以将数组A与数组B中所有的元素全都存入数组C中，且按从小到大排序 (注意：序列中相同的数全部保留并不计排列顺序)。例如，设数组A中有元素：2，5， 6，7，9；数组B中有元素2，3，4，7：则数组C中将有元素：2，2，3，4，5，6，7， 7， 9。【流程图】

2.阅读下列说明和流程图，填补流程图中的空缺，将解答填入答题纸的对应栏内。 【说明】 设有二维整数数组（矩阵）A[1:m,1:n],其每行元素从左到右是递增的，每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数X相等的数。如果找不到则输出“false”;只要找到一个（可能有多个）就输出“True”以及该元素的下标i和j（注意数组元素的下标从1开始）。 例如，在如下矩阵中查找整数8，则输出伟：True,4,1 2 4 6 9 4 5 9 10 6 7 10 12 8 9 11 13 流程图中采用的算法如下：从矩阵的右上角元素开始，按照一定的路线逐个取元素与给定整数X进行比较（必要时向左走一步或向下走一步取下一个元素），直到找到相等的数或超出矩阵范围（找不到）。【流程图】【问题】该算法的时间复杂数是（） 供选择答案：A.O（1） B.O（m+n） C.O（m*n） D,O（m²+n²）

3.阅读以下说明和流程图，填补流程图和问题中的空缺(1)～(5)，将解答填入答题纸的对应栏内。 【说明】 设整型数组A[1：N]每个元素的值都是1到N之间的正整数。一般来说，其中会有一些元素的值是重复的，也有些数未出现在数组中。下面流程图的功能是查缺查重，即找出A[1：N]中所有缺的或重复的整数，并计算其出现的次数（出现次数为0时表示缺）。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1：N]加上的一个映射，并用数组C[1：N]记录各整数出现的次数，需输出所有缺少的或重复的数及其出现的次数。【流程图】【问题】 如果数组A[1：5]的元素分别为{3，2，5，5，1}，则算法流程结束后输出结果为： (5) 。 输出格式为：缺少或重复的元素，次数（0表示缺少）

4.阅读以下说明和流程图将应填入(n)处的字句写在答题纸的对应栏内【说明】在一个矩阵中如果其零元素的个数远远多于其非零元素的个数时称这样的矩阵为稀疏矩阵稀疏矩阵通常采用三元组数组表示每个非零元素用一个三元组来表示即非零元素的行号列号和它的值然后按某种顺序将全部非零元素的三元组存于一个数组中例如对于以下二维数组其中三元数组a的第行元素的值分别存储稀疏矩阵x的行数列数和非零元素的个数下面的流程图描述了稀疏矩阵转换的过程【流程图】

更多“ 阅读以下说明和流程图，回答问题将解答填入对应栏。[说明]本流程图实现采用递归函数来求一个整数数组中从元素0到元素n中的最小值。该算法思想是这样的，首先我们假设有一个求数组中最小元素的函数，然后，在求某一具有n的元”相关问题

  • 第1题：

    试题三（共15分）

    阅读以下说明和C函数，回答问题 l和问题 2，将解答填入答题纸的对应栏内。

    【说明】

    对于具有n个元素的整型数组a，需要进行的处理是删除a中所有的值为 0的数组元素，并将a中所有的非 O元素按照原顺序连续地存储在数组空间的前端。下面分别用函数CompactArr_v1 和CompactArr v2来实现上述处理要求，函数的返回值为非零元素的个数。 函数CompactArr_vl(int a[]，int n)的处理思路是：先申请一个与数组a的大小相同的动态数组空间，然后顺序扫描数组a的每一个元素，将遇到的非O元素依次复制到动态数组空间中，最后再将动态数组中的元素传回数组a中。

    函数CompactArr_v2(int a[]，int n)的处理思路是：利用下标i（初值为 0）顺序扫描数组a的每一个元素，下标k（初值为0）表示数组 a中连续存储的非0元素的下标。扫描时，每遇到一个数组元素，i就增 1，而遇到非 0元素并将其前移后k才增 1。

    【问题1】 (12分)

    请根据说明中函数CompactArr_v1的处理思路填补空缺(1)～(3)，根据CompactArr_v2的处理

    思路填补空缺(4)。

    【问题2】（3分）

    请说明函数CompactArr vl存在的缺点。


    正确答案：
    试题三参考答案（共 15分）
    【问题 1】 (12分)
    (1) sizeof(int) （3分）
    若考生解答为一个正整数，则给 2分
    (2)temp[k++] 或*(temp+k++)或等价表示 （3分）
    (3) ik 或等价表示 （3分）
    (4)a[k++] 或*（a+k++）或等价表示 （3分）
    【问题 2】（3分）
    可能由于动态内存申请操作失败而导致函数功能无法实现，时间和空间效率低。
    注：考生仅回答出运行速度慢则给 2分，其他含义相同的描述可给满分或酌情给分。

  • 第2题：

    阅读以下说明和流程图，填补流程图中的空缺(1)～(9)，将解答填入对应栏内。1、【说明】 假设数组A中的各元素A(1)，A(2)，…，A(M)已经按从小到大排序(M≥1)；数组B中的各元素B(1)，B(2)，…，B(N)也已经按从小到大排序(N≥1)。执行下面的流程图后，可以将数组A与数组B中所有的元素全都存入数组C中，且按从小到大排序 (注意：序列中相同的数全部保留并不计排列顺序)。例如，设数组A中有元素：2，5， 6，7，9；数组B中有元素2，3，4，7：则数组C中将有元素：2，2，3，4，5，6，7， 7， 9。【流程图】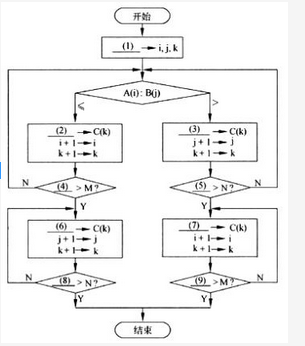


    答案：
    解析：
    （1）1(2)A(i)(3)B(j)(4)i(5)j(6)B(j)(7)A(i)(8)j(9)i
    【解析】

    这是最常见的一种合并排序方法。为对较大的序列进行排序，先将其分割成容量相当的几个部分，分别进行排序，最后再合并在一起。当然，这些排序要么都是升序，要么都是降序。本题全部是按升序排序的。 例如，为了将整副扑克牌按升序进行排序，先将其分割成两个部分(数量大致相当)，对每个部分完成升序排序后，就形成了两叠已排序的牌。如何将其合并呢?办法如下。 每次都比较各叠最上面的两张牌，取出比较小的，放入新堆，再继续比较。直到其中一堆空了，就将另一堆剩余的牌逐张放入新堆。新堆就是合并后的已完成排序的序列。 在数据排序时，遇到相同的数比较时，任取一个就可以了。 对本题来说，i、j、k是数组A、B、C的下标，初始时，都应该是1。因此，空(1)处应填写1。 将A(i)与B(j)进行比较后，如果A(i)≤B(j)，那么应该将A(i)→C(k)。这是升序的要求。因此，空(2)处应填A(i)。如果A(i)＞B(j)，则应将B(j)→C (k)。因此，空(3)处应填B(j)。 在A(i)→C(k)后，i应增加1，为下次取A(i)再比较做准备(k也需要增加1，为下次存入C(k)做准备)。这时，需要比较数组A是否已经取完，即判断i＞M是否成立。如果i＞M，则表示数组A中的元素已经全部取出，需要将数组B中剩余的元素逐个移入C(k)。因此，空(4)处应填i，空(6)处应填B(j)。数组B处的元素何时移完呢?这就需要判断i＞N是否成立。因此，空(8)处应填j。 同样，空(3)处将B(j)存入C(k)，直到，j＞N时数组B中的元素取完。此时，需要将数组A中剩余的元素逐个移入C(k)，直到i＞M时全部完成。因此，空(5)处应填j，空(7)处应填A(i)，空(9)处应填i。

  • 第3题：

    编写程序求含有N个元素一维数组的最大值、最小值及它们的下标。要求：数组元素的输入、求最大值最小值及它们的下标通过函数实现，结果在主函数中输出。


    D

  • 第4题：

    阅读以下说明和流程图，填补流程图和问题中的空缺(1)～(5)，将解答填入答题纸的对应栏内。【说明】设整型数组A[1：N]每个元素的值都是1到N之间的正整数。一般来说，其中会有一些元素的值是重复的，也有些数未出现在数组中。下面流程图的功能是查缺查重，即找出A[1：N]中所有缺的或重复的整数，并计算其出现的次数（出现次数为0时表示缺）。流程图中采用的算法思想是将数组A的下标与值看作是整数集[1：N]加上的一个映射，并用数组C[1：N]记录各整数出现的次数，需输出所有缺少的或重复的数及其出现的次数。【流程图】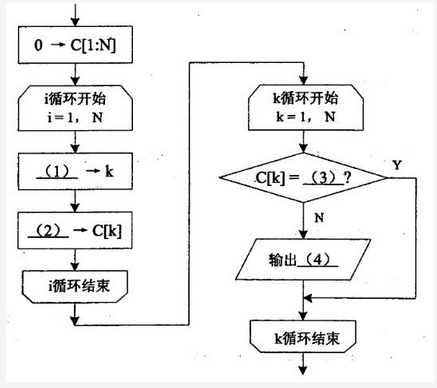

    【问题】 如果数组A[1：5]的元素分别为{3，2，5，5，1}，则算法流程结束后输出结果为： (5) 输出格式为：缺少或重复的元素，次数（0表示缺少）


    答案：
    解析：
    (1)A[i](2)C[k]+1(3)1(4)k和C[k](5)4,{1,1,1,0,2}
    【解析】

    (1)A[i](2)C[k]+1(3)1(4)k和C[k](5)4,{1,1,1,0,2}

  • 第5题：

    试题一（共 20 分）阅读下列说明和图，回答问题 1 至问题 3，将解答填入答题纸的对应栏内。【说明】设有二维整数数组（矩阵）A[1:m,1:n],其每行元素从左至右是递增的，每列元素从上到下是递增的。以下流程图旨在该矩阵中需找与给定整数 X 相等的数。如果找不到则输出“false”;只要找到一个（可能有多个）就输出“True”以及该元素的下标 i 和 j（注意数组元素的下标从 1 开始）。例如，在如下矩阵中查找整数 8，则输出伟：True,4,12 4 6 94 5 9 106 7 10 128 9 11 13流程图中采用的算法如下：从矩阵的右上角元素开始，按照一定的路线逐个取元素与给定整数 X 进行比较（必要时向左走一步或向下走一步取下一个元素），直到找到相等的数或超出矩阵范围（找不到）。【流程图】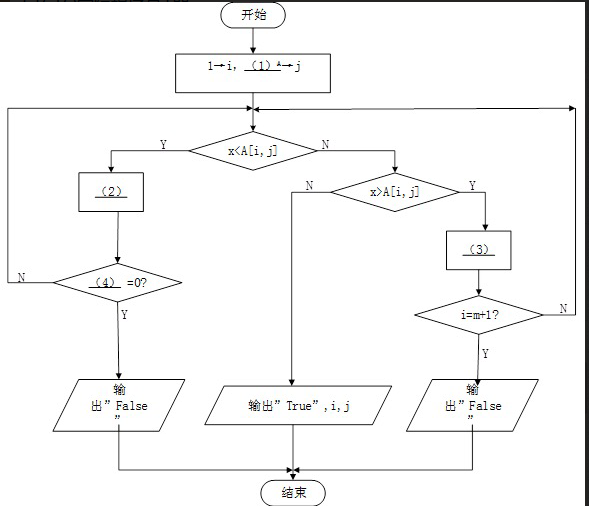

    【问题】该算法的时间复杂数是（）
    供选择答案：A.O（1） B.O（m+n） C.（m*n） D,O（m2+n2）


    答案：
    解析：
    （1）n（2）j-1→j（3）i+1→I（4）j（5）C
    【解析】

    读题，可以看出元素查找的过程为从右上角开始，往右或者往下进行查找。因此，初始值i=1，j=n。如果查找值小于右上角值，则往右移动一位再进行比较。所以，第二空填j-1→j 。接下来是判断什么时候跳出循环。此时，终止循环的条件是：j=0，也就是其从最右端移到了最左端。再看X

相关内容