在图4-1所示的系统中，R1、R2、R3为3个加工部件，每个加工部件的失效率均为λ，可靠性均为尺。则该系统的可靠性为(4)。若每个加工部件的平均无故障时间为5000小时，则该系统的平均无故障时间为(5)小时。A．(1-R2)3B．3(1-R2)C．R3(2-R)3D．1-3(1-R2)

题目

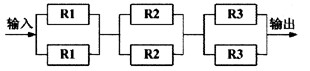
在图4-1所示的系统中，R1、R2、R3为3个加工部件，每个加工部件的失效率均为λ，可靠性均为尺。则该系统的可靠性为(4)。若每个加工部件的平均无故障时间为5000小时，则该系统的平均无故障时间为(5)小时。

A．(1-R2)3

B．3(1-R2)

C．R3(2-R)3

D．1-3(1-R2)

相似考题

1.由4个相同的独立部件组成一个并联连接系统, ,若组成系统的各部件单独工作时的可靠度相同,即R1=R2=R3=R4=0.9,则该并联系的总可靠度RS为。()A、RS=0.6491B、0.9999C、RS=0.9D、0.94

2.某计算机系统结构如下图所示，若所构成系统的每个部件的可靠度均为0.9，即R=0.9，则该系统的可靠度为______。A．B．C．D．

3.设一个系统由三个相同子系统并联构成，子系统的可靠性为0.9，平均无故障时间为10000小时，则系统可靠性为（1）和平均无故障时间为（2）小时。（1）A.0.729B.0.9C.0.999D.0.99（2）A.1.9999B.18000C.9000D.18333

4.某计算机系统的可靠性结构如下图所示，若所构成系统的每个部件的可靠度均为0.9，即R=0.9，则该系统的可靠度为______。A．0.9999945B．0.999945C．0.945D．0.9945

更多“ 在图4-1所示的系统中，R1、R2、R3为3个加工部件，每个加工部件的失效率均为λ，可靠性均为尺。则该系统的可靠性为(4)。若每个加工部件的平均无故障时间为5000小时，则该系统的平均无故障时间为(5)小时。A．”相关问题

第1题：

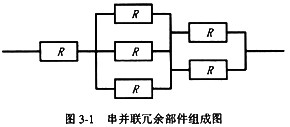
某高可靠性计算机系统由图3-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度R为(4)。
A．0.9999
B．0.9975
C．0.9475
D．0.8574

正确答案：C
解析：两个部件组成并联系统的可靠度计算公式为：1-(1-R1)(1-R2)=R1+R2-R1R2，两个部件组成串联系统的可靠度计算公式为：R1R2，其中R1、R2分别指单个系统的可靠度。本越R=0.95×(0.954-0.95-0.95×0.95)×0.95+(0.95+0.95-0.95×0.95)-0.95×(0.95+0.95-0.95×0.95))=0.95×0.9975×0.9999=0.99842=0.9475。
第2题：

● 设一个系统由三个相同子系统并联构成，子系统的可靠性为 0.9，平均无故障时间为 10000小时，则系统可靠性为__(2)__和平均无故障时间为__(3)__小时。
（2）
A. 0.729
B. 0.9
C. 0.999
D. 0.99
（3）
A. 1.9999
B. 18000
C. 9000
D. 18333

正确答案：C,D
试题分析
计算机系统是一个复杂的系统，而且影响其可靠性的因素也非常繁复，很难直接对其进行可靠性分析；
但通过建立适当的数学模型，把大系统分割成若干子系统，可以简化其分析过程。常见的系统可靠性数学模型有以下三种：
（1）串联系统：假设一个系统由 n个子系统组成，当且仅当所有的子系统都有能正常工作时，系统才能正常工作，这种系统称为串联系统，如图 1 所示。

设系统各个子系统的可靠性分别用R₁,R₂……,R_n表示，则系统的可靠性R=R₁×R₂×……×R_n.
如果系统的各个子系统的失效率分别用 λ₁ ，λ₂， ……，λ_n 来表示，则系统的失效率 λ=λ₁+λ₂+ ……+λ_n 。
（2）并联系统：假如一个系统由 n 个子系统组成，只要有一个子系统能够正常工作，系统就能正常工作，如图 2 所示。

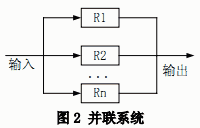
设系统各个子系统的可靠性分别用R₁,R₂……,Rn表示，则系统的可靠性R=1-(1-R₁)×(1-R₂)×……×(1-R_n).
假如所有的子系统的失效率均为λ，则系统的失效率为μ: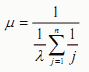

在并联系统中只有一个子系统是真正需要的，其余 n-1 个子系统称为冗余子系统，随着冗余子系统数量的增加，系统的平均无故障时间也增加了。
（3）模冗余系统：m 模冗余系统由 m个(m=2n+1 为奇数)相同的子系统和一个表决器组成，经过表决器表决后，m 个子系统中占多数相同结果的输出作为系统的输出，如图 3 所示。

在 m 个子系统中，只有 n+1 个或n+1个以上子系统能正常工作，系统就能正常工作，输出正确结果。假设表决器是完全可靠的，每个子系统的可靠性为 R0 ，则 m 模冗余系统的可靠性为:

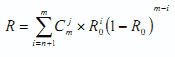
其中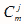为从 m 个元素中取 j 个元素的组合数。
在本题中采用了并联系统，且已知 R=0.9，λ=1/10000=1*10^-4小时，则系统可靠性为1-（1-0.9）³=0.999，系统平均无故障时间为 1/λ*(1+ 1/2+1/3)=18333 小时。
试题答案
（2） C （3） D
第3题：

某计算机系统的可靠性结构是如下图所示的双重串并联结构，若所构成系统的每个部件的可靠度均为0.9，即R=0.9，则该系统的可靠度为(3)。
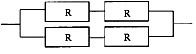
A．0.9997
B．0.9276
C．0.9639
D．0.6561

正确答案：C
解析：见公共试题Ⅱ(3)。
第4题：

● 设一个系统由三个相同子系统并联构成，每个子系统的可靠性为0.9，平均无故障时间为10000小时，则系统可靠性为（）和平均无故障时间为（）小时
（）
A. 0.729 B. 0.9
C. 0.999 D. 0.99
（）
A. 1.9999 B. 18000
C. 9000 D. 18333

正确答案：C,D
常见的系统可靠性数学模型有以下3种：①串联系统。假设一个系统由N个子系统组成，当且仅当所有的子系统都能正常工作时，系统才能正常工作，这种系统称为串联系统。设各子系统的可靠性为R1、R2、…Rn，则整个串联系统的可靠性为：R=R1×R2×…×Rn设各子系统的失效率为λ1、λ2…λn，则整个串联系统的失效率为：λ=λ1+λ2+…+λn②并联系统。假如一个系统由N个子系统组成，只要有一个子系统正常工作，系统就能正常工作，这样的系统称为并联系统。设各子系统的可靠性为R1、R2、…、Rn，则整个并联系统的可靠性为：R=1-（1-R1）（1-R2）…（1-Rn）设各子系统的失效率为λ，则整个并联系统的失效率为：分析R＝0.9λ=1/10000=1*10-4小时系统可靠性为1－(1－0.9)3＝0.9993平均无故障时间为：(1/λ)*∑(1/i)=1/λ*(1+1/2+1/3)=18333小时
第5题：

● 某计算机系统结构如下图所示，若所构成系统的每个部件的可靠度均为0.9，即R＝0.9，则该系统的可靠度为（4）。
（4）
A. 0.9801
B. 0.5905
C. 0.6561
D. 0.9624

正确答案：D
第6题：

设在图3-8和图3-9所示的系统中，R1，R2，R3为3个加工部件，每个加工部件的失效率均为丸，可靠性均为只。则图3-8系统的失效率为(20)，可靠性为(21)。图3-9中系统的失效率为(22)，可靠性为(23)。若每个加工部件的平均无故障时间为5000小时，则图3-9中系统的平均无故障时间为(24)小时。
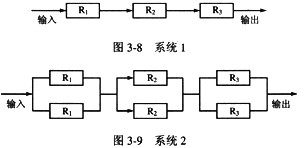
A．λ/3
B．λ3
C．3λ
D．1-λ3

正确答案：C
第7题：

某计算机系统的可靠性结构是如下图所示的双重串并联结构，若构成系统的每个部件的可靠度均为0.9，即 R=0.9。则该系统的可靠度为(13)。
A．0.9997
B．0.9276
C．0.9639
D．0.6561

正确答案：C
解析：见公共试题Ⅱ(3)。
第8题：

分别考虑如图3-6的a，b，c和d所示的系统。若其中单个I/O的可靠性都是R1，单个CPU的可靠性都是R2，单个MEM的可靠性都是R3，而三选二表决器的可靠性为1，则图a系统的可靠性为(10)，图b系统的可靠性为(11)，图c系统的可靠性为(12)，图d系统的可靠性为(13)。
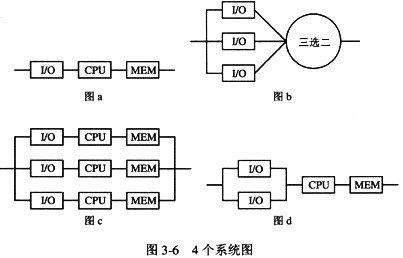
对于如图3-6所示的d所示系统，若单个I/O，CPU和MEM的平均无故障间隔时间(MTBF)分别为1000小时、1500小时和3000小时，则系统的MTBF为(14)小时。
A．
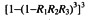
B．
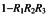
C．
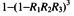
D．
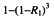
E．

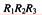正确答案：E
第9题：

在图4-9所示的计算机系统中，R1、R2、R3分别为3种不同的加工部件，但每个加工部件的失效率均为λ，可靠性均为R，则该系统的可靠性为(1)。若每个加工部件的平均无故障时间为5000小时，则该系统的平均无故障时间为(2)小时。
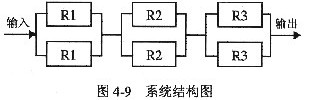
(1)
A．(1-R2)3
B．3(1-R2)
C．R3(2-R)3
D．1-3(1-R2)

正确答案：C
第10题：

某高可靠性计算机系统由下图所示的冗余部件构成。若每个部件的千小时可靠度 R均为0.9，则该计算机系统的千小时可靠度为(18)；该计算机系统的失效率丸可使用(19)来计算。注：t表示时间。
A．0.656
B．0.729
C．0.801
D．0.864

正确答案：C
解析：从可靠性角度分析，该计算机系统是一个并串联系统，其中有三个部件并联冗余构成一个功能部件，其可靠度为0.999；两个可靠度为0.9的部件并联冗余，其可靠度为0.99。这两个并联冗余的部件再与可靠度为0.9的两个部件串联构成该计算机系统，故该计算机系统的可靠度为；
Rs=0.9×0.999×0.99×0.9=0.801
根据可靠度的定义：R(t)＝e-λt，失效率入可以用式-InR/t来进行计算。
第11题：

某高可靠性计算机系统由图6-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度R为（）。

A.0.9999
B.0.9975
C.0.9475
D.0.8574

答案：C
解析：
系统可靠性计算，这是串并联混合系统，每个R可靠性是0.95，总可靠性是 0.95*（1-（1-0.95）^3）（1-（1-0.95）^2）=0.9475.本题计算有个小技巧，这种复杂的计算先不要硬算，看下相乘的结果，肯定是小于0.95的，也不能太离谱。
第12题：

部件的可靠性通常可以用平均无故障时间来衡量。

正确答案:正确
第13题：

某高可靠性计算机系统由图2-1所示的冗余部件构成，若每个部件的千小时可靠度为0.95，则该系统的千小时可靠度只为(4)。
A．0.9999
B．0.9975
C．0.9475
D．0.8574

正确答案：C
解析：系统可靠度计算，并联系统：1-(1-R1)(1-R2)=R1+R2-R1R2，串联系统：R1R2，其中R1、R2分别指单个系统的可靠度。本题R=0.95×[0.95+0.95-0.95×0.95]×[0.95+[0.95+0.95-0.95×0.95]-0.95×[0.95+0.95-0.95×0.95]]=0.95×0.9975×0.9999=0.99842=0.9475
第14题：

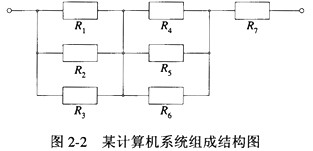
某计算机系统由如图2-2所示的部件构成，其中部件R1～R3的千小时可靠度均为0.6，部件R4～R6的千小时可靠度均为0.7，R7的千小时可靠度为0.95，则该系统的千小时可靠度约为(4)。
A．0.865
B．0.936
C．0.973
D．0.999

正确答案：A
解析：该计算机系统的可靠性结构是一个典型的串并联结构。部件凡和部件尺：组成并联系统的可靠度计算公式为：1-(1-R1)(1-R2)=R1+R2-R1R2，而这两个部件组成串联系统的可靠度计算公式为：R1×R2。计算公式中的R1、R2分别是单个部件的可靠度。由于系统中每个部件的千小时可靠度均小于1，而图2-24系统的总可靠度可看成3个子系统串联的可靠度，这3个子系统分别为单个部件R7、3个可靠度相同的部件R1组成的并联子系统及3个可靠度相同的部件R4组成的并联子系统。因此系统的总可靠度应小于单个部件R7的千小时可靠度0.95，即可先排除选项C、D。由于部件R1～R3的千小时可靠度均为0.6，这3个部件所组成的并联系统的千小时可靠度约为 1-(1-R1)×(1-R2)×(1-R3)=1-(1-R1)³=1-(1-0.6)³=0.936。同理可得，部件R4-R6所组成的并联系统的千小时可靠度约为1-(1-R4)×(1-R5)×(1-R6)=1- (1-R4)³=1-(1-0.7)³=0.973。因此整个系统的千小时可靠度约为(1-(1-R1)³)×(1-(1-R4)³)×R7=0.936×0.973×0.95≈0.8652。
第15题：

某计算机系统由如图8-1所示的部件构成，其中部件R1至R3的千小时可靠度均为0.6，部件R4至 R6的千小时可靠度均为0.7，R7的千小时可靠度为0.95，则该系统的千小时可靠度约为(4)。
A．0.865
B．0.936
C．0.973
D．0.999

正确答案：A
解析：该计算机系统的可靠性结构是一个典型的串并联结构，其中部件R1至R3的千小时可靠度均为0.6，这3个部件所组成的并联系统的千小时可靠度约为1-(1-R1)×(1-R2)×(1-R3)=1-(1-R1)3=1-(1-0.6)3=0.936。同理可得，部件R4～R6所组成的并联系统的千小时可靠度约为1-(1-R4)×(1-R5)×(1-R6)=1-(1-R4)3=1-(1-0.7)3=0.973。因此整个系统的千小时可靠度约为(1-(1-R1)3)×(1-(1-R4)3)×R7=0.936×0.973×0.95≈0.8652。
第16题：

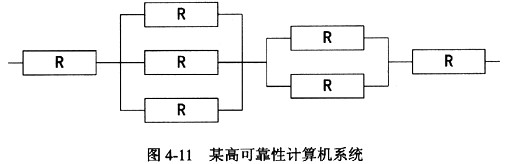
某高可靠性计算机系统由图4-11所示的冗余部件构成。若每个部件的千小时可靠度R均为0.9，则该计算机系统的千小时可靠度为(66)，该计算机系统的失效率λ可使用(67)来计算。(注：t表示时间)
A．0.656
B．0.729
C．0.801
D．0.864

正确答案：C
第17题：

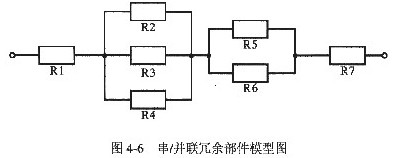
某高可靠性计算机系统由图4-6所示的冗余部件构成。若每个部件的千小时可靠度尺均为0.9，则该计算机系统的千小时可靠度为(1)；该计算机系统的失效率可使用(2)来计算。(注：t表示时间)
(1)
A．0.656
B．0.729
C．0.801
D．0.864

正确答案：C
第18题：

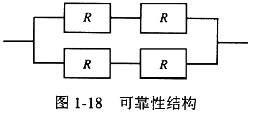
某计算机系统的可靠性结构是如图1-18所示的双重串并联结构，若所构成系统的每个部件的可靠性为0.9，即R=0.9，则系统的可靠性为 ______。
A．0.9997
B．0.9276
C．0.9639
D．0.6561

正确答案：C
解析：计算机系统的可靠性是指从它开始运行(t=0)到某时刻，这段时间内能正常运行的概率，用R(t)表示。计算机系统是一个复杂的系统，而且影响其可靠性的因素也非常复杂，因此需要通过建立适当的数学模型简化其分析。常见的数学模型有：串联系统、并联系统和N模冗余系统。串联系统：当且仅当所有的子系统都能正常工作时系统才能正常工作。系统可靠性由下式计算：R=R1×R2×...×RN并联系统：只要有一个子系统正常工作，系统就能正常工作。系统可靠性由下式计算：R=1-(1-R1)×(1-R2)×…×(1-RN)N模冗余系统：N模冗余系统由N(N=2n+1)个相同的子系统和一个表决器组成，表决器把N个子系统中占多数相同结果的输出作为系统的输出。在N个子系统中，只要有n+1个或n+1个以上子系统能正常工作，系统就能正常工作。系统可靠性由下式计算：本题系统可靠性Rsys=1-(1-R2)(1-R2)=R2(2-R2)=0.9639。
第19题：

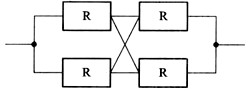
某计算机系统由图5-35所示的部件构成，假定每个部件的千小时可靠度R均为0.9，则该系统的千小时可靠度约为______。
A．0.9801
B．0.951
C．0.9
D．0.99

正确答案：A
解析：不要被两并联子系统之间的网状连线所误导，其实可以将这些网状连线“拧成”一根两头分叉的导线来看待，其等价结构图如图5-37所示。两个R并联的可靠度为：1-(1-0.9)2=0.99。我们可以将两个并联的R部件看成一个部件R1，R1的可靠度为0.99，所以该系统的可靠度为：0.99×0.99=0.9801。所以答案为A。
第20题：

在下图所示的系统中，若部件R1的可靠性是0.98，R2的可靠性是0.95，R3的可靠性是0.9，则整个系统的可靠性约为(6)；若各个部件的失效率都是L那么整个系统的失效率是(7)。
A．0.84
B．0.92
C．0.94
D．0.95

正确答案：B
解析：先计算由两个R3构成的并联系统的可靠性R=1-(1-0.9)×(1-0.9)=0.99，再计算整个串联系统的可靠性R=0.98×0.95×0.99=0.92。
第21题：

三个可靠性R均为0.8的部件串联构成一个系统，如图1-20所示则该系统的可靠性为______ 。
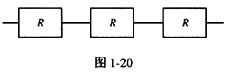
A．0.24
B．0.512
C．0.8
D．0.992

正确答案：B
解析：这一题考查串联系统可靠性计算，系统可靠性及为三部分可靠性的乘积。
第22题：

某系统由下图所示的冗余部件构成。若每个部件的千小时可靠度都为R，则该系统的千小时可靠度为( )。

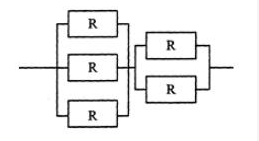
答案：B
解析：
本题考查系统可靠性。计算机系统是一个复杂的系统，而且影响其可靠性的因素也非常繁复，很难直接对其进行可靠性分析。若采用串联方式，则系统可靠性为每个部件的乘积R=R1×R2×R3×…×Rn；若采用并联方式，则系统的可靠性为R=1-（1-R1）×（1-R2）×（1-R3）×…×（1-Rn）。在本题中，既有并联又有串联，计算时首先我们要分别计算图中两个并联后的可靠度，它们分别为（1-（1-R）3）和（1-（1-R）2）。，然后是两者串联，根据串联的计算公式，可得系统的可靠度为（1-（1-R）3）（1-（1-R）2）。
第23题：

某计算机系统各组成部件的可靠性模型由下图所示，若每个部件的千小时可靠度都为R，则该计算机系统的千小时可靠度为（）。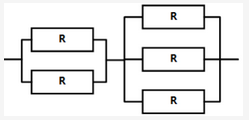

A. （1-R2）（1- R3）
B. （1-R2）+（1- R3）
C. （1-（1-R）2）（1-（1-R）3）
D. （1-（1-R）2）+（1-（1-R）3）

答案：C
解析：
解析：串联系统可靠性公式为：R=R1×R2×...×Rn

并联系统可靠性公式为：R=1-（1-R1）×（1-R2）×...×（1-Rn）

系统分为两个部分，第一部分两个R并联，第二部分三个R并联，最后两个部分串联组成整个系统。

题目

相似考题

相关内容