已知x=-127,若采用八位机器码表示,则[X]原=(6),[X]补=(7)。(53)A.10000001B.01111111C.11111111D.10000000
题目
已知x=-127,若采用八位机器码表示,则[X]原=(6),[X]补=(7)。
(53)
A.10000001
B.01111111
C.11111111
D.10000000
相似考题
更多“已知x=-127,若采用八位机器码表示,则[X]原=(6),[X]补=(7)。(53)A.10000001B.01111111C.11111111D.10000000”相关问题
-
第1题:
设机器码的长度为8位,已知x,z为带符号纯整数,y为带符号纯小数,[X]原=[Y]补=[Z]移=11111111,求出x、y、z的十进制真值:X=(11)Y=(12),Z=(13)。
A.127
B.-1
C.-127
D.1
正确答案:C
解析:X的原码为11111111,易得X为负数,真值为-01111111=-127。Y的补码为11111111,Y也是负数,所以Y等于Y的补码减1,即1.1111111-10=-0.0000001=-1/128。Z为定点整数,所以Z=11111111-10000000=01111111=127。 -
第2题:
已知x=-105/128,若采用8位机器码表示,则[x]补=(6)。
A.10010111
B.11010101
C.11101010
D.10100111
正确答案:A
解析:这一类型的题目考查的知识点是小数的原码和补码的表示方法。在机器码的表示中,小数的表示方法是:数的最左面是符号位,对于原码、反码或补码,如果该小数是正数,则该符号位为0,如果该小数是负数,则该符号位为1;其余各位为该小数的数据位,从左起,第2位的权值为1/2,第3位的权值为1/4,依此类推。解答此类题目的一般思路是:将给定的分式分解成多个分式之和的形式,每个分式的分子为1,分母为2的幂次,这样可以确定其原码表示。而使用补码表示一个小数时,只要将该数除符号位之外求反,然后加1,就可以得到该数的补码表示。针对这道题目,由于x=-105/128=-(64/128+32/128+8/128+1/128)=-(1/2+1/4+1/6+1/128)。根据上面的分析,可以确定x的原码为11101001。对原码求反(符号位不变)后的值为10010110,加1得到该数的补码为10010111。所以本试题的正确答案是选项A。 -
第3题:
已知x = -53/64,若采用8位定点机器码表示,则【x】原=( ),【x】补=( )。
A.01101101 B.11101010 C.11100010D.01100011A.11000011B.11101010C.10011110D.10010110
正确答案:B,D
-
第4题:
设机器码的长度为8位,已知X、Z为带符号的纯整数,Y为带符号的纯小数,[X]原=[Y]补=[Z]移=11111111,求出X、Y、Z的十进制真值为X=(16),Y=(17), Z=(18)。
A.-1
B.127
C.-127
D.1
正确答案:C
-
第5题:
● 已知 X = –121,若采用8位机器码表示,则[X]原= (3) , [X]补= (4) 。
(3)
A. 11001001
B. 11111001
C. 01111001
D. 01011001
(4)
A. 10110111
B. 10000111
C. 10100111
D. 01111001
正确答案:B,B
-
第6题:
若X=-127,Y=-1,字长N=8,则[X+Y]补是
A.80H
B.00H
C.0FDH
D.7EH
正确答案:B
-
第7题:
设机器码的长度为8位,已知[X]原=[Y]补=1111 1111,且X和Y都是带符号的整数,则X和Y的真值分别为( )。A.-127,-127
B.-1,-127
C.-127,-1
D.-1,-1答案:C解析:其中-127的原码是1111 1111。而-1的补码表示为:1111 1111。 -
第8题:
已知x=-105/128,若采用8位机器码表示,则[x]补= ( ) 。A.10010111
B.11010101
C.11101010
D.10100111答案:A解析:这一类型的题目考查的知识点是小数的原码和补码的表示方法。在机器码的表示中,小数的表示方法是:数的最左面是符号位,对于原码、反码或补码,如果该小数是正数,则该符号位为0,如果该小数是负数,则该符号位为1;其余各位为该小数的数据位,从左起,第2位的权值为1/2,第3位的权值为1/4,依此类推。解答此类题目的一般思路是:将给定的分式分解成多个分式之和的形式,每个分式的分子为1,分母为2的幂次,这样可以确定其原码表示。而使用补码表示一个小数时,只要将该数除符号位之外求反,然后加1,就可以得到该数的补码表示。针对这道题目,由于x=-105/128=-(64/128+32/128+8/128+1/128)=-(1/2+1/4+1/6+1/128)。根据上面的分析,可以确定x的原码为11101001。对原码求反(符号位不变)后的值为10010110,加1得到该数的补码为10010111。所以本试题的正确答案是选项A。 -
第9题:
已知x = -53/64,若采用8位定点机器码表示,则[x]原=(21),[x]补=(22)。A.01101101
B.11101010
C.11100010
D.01100011答案:B解析:
-
第10题:
已知X=-100,若采用8位机器码表示,则X的原码位为(请作答此空),X的补码为( )A. 11100100
B. 01001001
C. 10011100
D. 00011001答案:A解析:-100的原码11100100,补码为原码取反+1,因此为A -
第11题:
设机器码的长度为8位,已知x和y为有符号纯整数,z为有符号纯小数,[x]原=[y]移=补[z]F=11111111,求x、y、z的十进制真值为:x=(1),y=(2),z=(3)。空白(2)处应选择()
- A、-1
- B、127
- C、-127
- D、1
正确答案:B -
第12题:
单选题设机器码的长度为8位,已知x和y为有符号纯整数,z为有符号纯小数,[x]原=[y]移=补[z]F=11111111,求x、y、z的十进制真值为:x=(1),y=(2),z=(3)。空白(3)处应选择()A-1
B127
C-127
D1
正确答案: B解析: 暂无解析 -
第13题:
已知x=-69,若采用8位机器码表示,则[X]补=(1)。
A.1000101
B.10111010
C.10111011
D.11000101
正确答案:C
解析:由于-6910=-(64+4+1)10=-010001012,根据定义,数值X的原码记为[X]原。如果机器字长为n(即采用n个二进制位表示数据),则最高位是符号位,0表示正号,1表示负号,其余的n-1位表示数值的绝对值。因此[X]原=(11000101)2。数值X的补码记作[X]补,如果机器字长为n,则最高位为符号位,0表示正号,1表示负号,正数的补码与其原码和反码相同,负数的补码则等于其反码的末尾加1。因此[X]补=(10111011)2。 -
第14题:
已知x=-61/128,若采用8位定点机器码表示,则[X]原=(22)。
A.00111101
B.10111101
C.10011111
D.00111110
正确答案:B
整个计算过程如下:61/128=0.47656250.4765625*2=0.953125整数为00.953125*2=1.90625整数为10.90625*2=1.8125整数为10.8125*2=1.625整数为10.625*2=1.25整数为10.25*2=0.5整数为00.5*2=1整数为1,小数为0因为是负数,其符号位为1,因此原码是10111101。 -
第15题:
己知 x = -31/64,若采用8位定点机器码表示,则[x]原=( ),[x]补=( )。
A. 01001100B. 10111110C. 11000010D. 01000010A. 01001100B. 10111110C. 11000010D. 01000010
正确答案:B,C
-
第16题:
己知 X= -79/128,若采用 8位定点机器码表示,则 [x]补 = ( )。
A. 1.1001111B. 0.1001111C. 1.0110001D. 0.1110001
正确答案:C
-
第17题:
●已知x=61/128,若采用8位定点机器码表示,则[X]原=(22)。
(22)A. 00111101
B. 10111101
C. 10011111
D. 00111110
正确答案:B
-
第18题:
已知x=-31/64,若采用8位定点机器码表示,则[x]原=(请作答此空),[x]补=( )。A.01001100
B.10111110
C.11000010
D.01000010答案:B解析:本题考查计算机系统数据表示基础知识。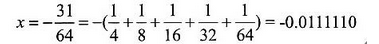
[x]原=10111110,[x]补=11000010 -
第19题:
已知x = -53/64,若采用8位定点机器码表示,则[x]原=(),[x]补=(22)。A.11000011
B.11101010
C.10011110
D.10010110答案:D解析:本题考查计算机系统基础知识。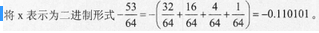
原码表示的规定是:如果机器字长为n(即釆用n个二进制位表示数据),则最髙位是符号位,0表示正号,1表示负号,其余的n-1位表示数值的绝对值。因此,[x]原=1.1101010
补码表示的规定是:如果机器字长为n,则最高位为符号位,0表示正号,1表示负号,其余的n-1位表示数值。正数的补码与其原码和反码相同,负数的补码则等于其原码数值部分各位取反,最后在末尾加1。g此,[x]补=1.0010110。 -
第20题:
已知x=-31/64,若采用8位定点机器码表示,则[x]原=( ),[x]补=(请作答此空)。A.01001 100
B.10111110
C.11000010
D.01000010答案:C解析:
-
第21题:
已知x=一53/64,若采用8位定点机器码表示,则[x]原=( ),[x]补=(请作答此空)。A.11000011
B.11101010
C.10011110
D.10010110答案:D解析:符号位1表示-,0表示+。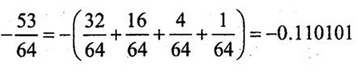
负数的补码=原码按位取反+1。后面尾数不足,可以补0. -
第22题:
已知x=一53/64,若采用8位定点机器码表示,则[x]原=(请作答此空),[x]补=( )。A. 01101101
B. 11101010
C. 11100010
D. 01100011答案:B解析:符号位1表示-,0表示+。
负数的补码=原码按位取反+1。后面尾数不足,可以补0. -
第23题:
若X=-1,Y=-127,字长n=16,则[X]补=()H,[Y]补=()H,[X+Y]补=()H,[X-Y]补=()H。
正确答案:0FFFFH;0FF81H;0FF80H;007EH
