某计算机系统的机构如下图所示，其中，Pui（i=1，……，n）为处理单元，CU为控制部件，MMj（j=1，……，n）为存储部件。该计算机（ ）。A.通过时间重叠实现并行性 B.通过资源重复实现并行性 C.通过资源共享实现并行性 D.通过精简指令系统实现并行性

题目
某计算机系统的机构如下图所示，其中，Pui（i=1，……，n）为处理单元，CU为控制部件，MMj（j=1，……，n）为存储部件。该计算机（ ）。


A.通过时间重叠实现并行性
B.通过资源重复实现并行性
C.通过资源共享实现并行性
D.通过精简指令系统实现并行性
相似考题

1.设二维数组a[0…m－1][0…n－1]按列优先顺序存储在首地址为LOC(a[0][0])的存储区域中,每个元素占d个单元,则a[i][j]的地址为()A.LOC（a［0］［0］）+（j×n+i）×dB.LOC（a［0］［0］）+（j×m+i）×dC.LOC（a［0］［0］）+（（j-1）×n+i-1）×dD.LOC（a［0］［0］）+（（j-1）×m+i-1）×d

2.某计算机系统的结构如下图所示，按照弗林(Michael J.Flynn)提出的分类法，它属于(17)，其中，PUi(i=1，…，n)为处理单元，CU为控制部件，MMj(j=1，…，n)为存储部件。该计算机(18)。A．单指令流单数据流计算机(SISD)B．单指令流多数据流计算机(SIMD)C．多指令流单数据流计算机(MISD)D．多指令流多数据流计算机(MIMD)

3.●设数组a[1．．n，1．m](n>1，m>1)中的元素以行为主序存放，每个元素占用1个存储单元，则数组元素a[i，j](1≤i≤n，1≤j≤m)相对于数组空间首地址的偏移量为(14)。(14) A. (i-1)*m+j-1B. (i-1)*n+j-1C. (j-1)*m+i-1D. (j-1)*n+i-1

4.● 设数组a[0..m,1..n]的每个元素占用1个存储单元，若元素按行存储，则数组元素a[i,j]（0≤i≤m，1≤j≤n）相对于数组空间首地址的偏移量为 （32） 。（32）A. (i+1)*n+jB. i*n+j-1C. i*m+jD. i*(m+1)+j-1

更多“某计算机系统的机构如下图所示，其中，Pui（i=1，……，n）为处理单元，CU为控制部件，MMj（j=1，……，n）为存储部件。该计算机（ ）。 ”相关问题

  • 第1题：

    ●若二维数组arr[1..M，1..N】的首地址为base，数组元素按列存储且每个元素占用K个存储单元，则元素arr[i，j]在该数组空间的地址为 (21)。

    (21)

    A. base+((i-1)*M+j-1)*K

    B．base+((i-1)*N+j-1)*K

    C.base+((j-1)*M+i-1)*K

    D.base+((j-1)*N+i-1)*K


    正确答案：C

  • 第2题：

    设n行n列的下三角矩阵A已压缩到一维数组B[1...n(n+1)/2]中，若按行为主序存储，则A[i,j]对应的B中存储位置为(48)。

    A．i(i-1)/2+j

    B．j(j-1)/2+i

    C．i(i+D)/2+j

    D．j(j+1)/2+i


    正确答案：A
    解析：按行主序则第1行有1个元素，第2行有2个元素，...第i-1行有i-1个元素，第i行有i个元素，对应数组B[1...n(n+1)/2]的位置即为这些元素的个数i(i-1)/2+j。

  • 第3题：

    ● 某计算机系统的结构如下图所示，按照弗林（Michael J.Flynn）提出的分类法，它属于 （17） ，其中，PUi（i=1,…,n）为处理单元，CU为控制部件，MM j（j=1,…,n）为存储部件。该计算机 （18） 。

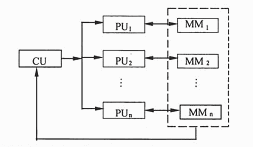
    （17）

    A. 单指令流单数据流计算机（SISD）

    B. 单指令流多数据流计算机（SIMD）

    C. 多指令流单数据流计算机（MISD）

    D. 多指令流多数据流计算机（MIMD）

    （18）

    A. 通过时间重叠实现并行性

    B. 通过资源重复实现并行性

    C. 通过资源共享实现并行性

    D. 通过精简指令系统实现并行性


    正确答案：B,B

  • 第4题：

    设数组a[0．n-1,0．．m-1](n>1，m>1)中的元素以行为主序存放，每个元素占用4个存储单元，则数组元素a[i,j](0≤i<n，0≤j<m)的存储位置相对于数组空间首地址的偏移量为 （ ）。

    A.(j*m+i)*4B.(i*m+j)*4C.(j*n+i)*4D.(i*n+j)*4


    正确答案：B

  • 第5题：

    设数组a[1...n，1.....m](n>1，m>1)中的元素以列为主序存放，每个元素占用1个存储 单元，则数组元素a[ij](1≤i≤n，l≤j≤m)桂对于数组空间首地址的偏移量为(35)。

    A.(i-l)*m+j-l

    B.(i-l)*n+j-l

    C.O-l)*m+i-l

    D.(j-l)*n+i-l


    正确答案：D
    本题考查程序语言基础知识。存储数组元素时，需要将元素按照某种顺序排列。对于二维及多维数组，则有按行存储和按列存储两种方式，其不同在于同一个元素相对于数组空间起始位置的偏移量不同。本问题中n行m列的二维数组a[1...n，1..m]是按列存储，则对于元素a[ij]来说，它之前有完整的j一1列、每列n个元素，在第j列上排在a[ij]之前的元素个数是j-1个，因此排列在a[ij]之前的元素个数为(j-l)*n+i-l：由于每个元素占一个单元，该表达式的值就是偏移量。

  • 第6题：

    设数组A[1..m,1..n]的每个元素占用1个存储单元，对于数组元素A[i,j](1≤i≤m，1≤j≤n)，在按行存储方式下，其相对于数组空间首地址的偏移量为(请作答此空)；在按列存储方式下，其相对于数组空间首地址的偏移量为( )。

    A.i*(n-1)+j
    B.(i-1)*n+j-1
    C.i*(m-1)+j
    D.(i-1)*m+j-1

    答案：B
    解析：
    本题考查数据结构基础知识。数组A[1..m,1..n]的元素排列如下。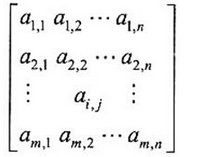

    解答该问题需先计算排列在a[i,j]之前的元素个数。
    按行方式存储下，元素a[i,j]之前有i-1行，每行n个元素，在第i行上a[i,j]之前有j-1个元素，因此，a[i,j]之前共有(i-1)*n+j-1个元素。
    在按列存储方式下，元素a[i,j]之前有i-1列，每列m个元素，在a[i,j]所在列(即第j列)，排在它之前的元素有i-1个，因此，a[i,j]之前共有(i-1)*m+i-1个元素。
    数组中指定元素的存储位置相对于数组空间首地址的偏移量等于k*d，其中k为排在该元素前的元素个数，d为每个元素占用的存储单元数。

  • 第7题：

    设数组a[1..m,1..n]（m＞1，n＞1）中的元素按行存放，每个元素占用1个存储单元，则数组元素a[i,j]（1≤i≤m，1≤j≤n）相对于数组首元素的偏移量为（ ）。

    A.(i-1)*m+j-1
    B.(i-1)*n+j-1
    C.(j-1)*m+i-1
    D.(j-1)*n+i-1

    答案：B
    解析：
    存储数组元素时，需要将元素按照某种顺序排列。对于二维及多维数组，则有按行存储和按列存储两种方式，其不同在于同一个元素相对于数组空间起始位置的偏移量不同。本问题中 n 行 m 列的二维数组 a[1..m，1..n]是按行存储，则对于元素 a[i，j]来说，它之前有完整的 i-1 列、每行n 个元素，在第 i行上排在 a[i，j]之前的元素个数是 j-1 个，因此排列在a[i，j]之前的元素个数为 (i-1)*n+j-1，由于每个元素占一个单元，该表达式的值就是偏移量。

  • 第8题：

    若二维数组arr[1…M，1…N]的首地址为base，数组元素按列存储且每个元素占用K个存储单元，则元素arr[i，j]在该数组空间的地址为（ ）。

    A.base+（（i一1）*M*j-i）*K
    B.b ase+（（i-1）*N+j-1）*K
    C.baSe+（（j-l）*M十i-1）*K
    D.base+（（j-1）*N+i-1）*K

    答案：C
    解析：

  • 第9题：

    假设铁路自动售票系统有 n 个售票终端，该系统为每个售票终端创建一个进程 Pi（i=1,2,…,n）管理车票销售过程。假设 Tj（j=1,2,…,m）单元存放某日某趟车的车票剩余票数，Temp 为 Pi进程的临时工作单元，x 为某用户的购票张数。Pi进程的工作流程如下图所示， 用 P 操作和Ⅴ操作实现进程间的同步与互斥。初始化时系统应将信号量 S 赋值为（请作答此空）。 图中（a）、（b）和（c）处应分别填入（ ）。


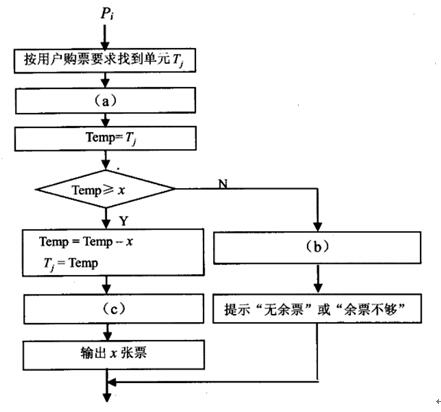    A.n-1
    B.0
    C.1
    D.2

    答案：C
    解析：
    按照用户购票要求找到了单元，那么（a）应该执行P操作来申请一个资源，互斥操作的信号量初值一般为1或者资源的数量，剩下的（b）（c）都应该是V操作，释放资源。

  • 第10题：

    某n阶的三对角矩阵A如下图所示，按行将元素存储在一堆数组M中，设A1，1存储在M[1],那么ai,j（I<=i,j<=n且ai,j位于三条对角线中），存储在M（ ）


    A.i+2j
    B.2i+j
    C.i+2j-2
    D.2i+j-2

    答案：D
    解析：
    这类题型可以直接用实例来排除错误选项。a11存在M[1]，将i=1，j=1带入选项，A,B不正确。然后根据题干描述按行存储，下一元素应该是a12，存放在M[2]中，将i=1，j=2带入选项，只有D选项符合题意

  • 第11题：

    单选题
    设二维数组A[0…m-1][0…n-1]按行优先顺序存储在内存中，第一个元素的地址为p，每个元素占k个字节，则元素aij的地址为（）。
    A

    p+[i*n+j-1]*k

    B

    p+[（i-1）*n+j-1]*k

    C

    p+[（j-1）*n+i-1]*k

    D

    p+[j*n+i-1]*k


    正确答案： C
    解析： 暂无解析

  • 第12题：

    单选题
    设二维数组a［0…m-1］［0…n-1］按列优先顺序存储在首地址为LOC（a［0］［0］）的存储区域中，每个元素占d个单元，则a［i］［j］的地址为（）
    A

    LOC（a［0］［0］）+（j×n+i）×d

    B

    LOC（a［0］［0］）+（j×m+i）×d

    C

    LOC（a［0］［0］）+（（j-1）×n+i-1）×d

    D

    LOC（a［0］［0］）+（（j-1）×m+i-1）×d


    正确答案： C
    解析： 暂无解析

  • 第13题：

    按行优先顺序存储下三角矩阵的非零元素，则计算非零元素aij(1≤j≤n)的地址的公式为其中入为每个数组元素所占用的存储单元空间。

    A．LOC(aij)=LOC(a11)+[i×(i+1)/2+j]*λ

    B．LOC(aij)=LOC(a11)+[i×(i+1)/2+(j-1)]*λ

    C．LOC(aij)=LOC(a11)+[i×(i-1)/2+j]*λ

    D．LOC(aij)=LOC(a11)+[i×(i+1)/2+(j-1))]*λ 下列题目基于下图所示的二叉树：


    正确答案：D
    解析：如果按行优先顺序列出下三角矩阵中的非零元素，得到如下序列 A11，A21，A22，...An1，An2…Ann，把它顺序存储在内存中，第一行到第i行共有非零元素的个数为[i×(i-1)/2]，因此非零元素Aij(1≤j≤i≤n)的地址的公式为LOC(Aij)：LOC (A11)+(i×(i-1)/2+(j-1)]*λ。因此本题正确答案是选项D。实际上这相当于是个等差数列求和的问题。鉴于题目的特殊性，可以考虑用特例法来解，这就是令i=1，j= 1，检验哪个选项是正确的。

  • 第14题：

    ● 若二维数组arr[1..M，1..N]的首地址为base，数组元素按列存储且每个元素占用K个存储单元，则元素arr[i，j]在该数组空间的地址为 （21） 。

    A．base+（（i-1）*M+j-i）*K

    B．base+（（i-1）*N+j-1）*K

    C．base+（（j-1）*M+i-1）*K

    D．base+（（j-1）*N+i-1）*K


    正确答案：C

     

  • 第15题：

    设数组a[0．．m，1．．n]的每个元素占用1个存储单元，若元素按行存储，则数组元素a[i，j](0≤i≤m，1≤j≤n)相对于数组空间首地址的偏移量为( )。

    A．(i+1)*n+j

    B．i*n+j-l

    C．i*m+j

    D．i*(m+1)+j-1


    正确答案：B
    解析：因为是按行存储，所以是i×n，又因为列是从1开始，所以是j-1。最终答案为i*n+j-l。

  • 第16题：

    设数组 A[ 1..m，1...n.] 的每个元素占用 1 个存储单元，对于数组元素 A[i，j] (1≤i≤m≤1≤j≤n)，在按行存储方式下，其相对于数组空间首地址的偏移量为（ ）；在按列存储方式下，其相对于数组空间首地址的偏移量为（ ）。

    A. i*(n-1)+j B. (i-1)*n+j-1 C. i*(m-1)+j D. (i-1)*m+j-1A. j*(n-1)+i B. (j-1)*n+i-1 C. j*(m-1)+iD. (j-1)*m+i-1


    正确答案：B,D

  • 第17题：

    设数组A[1..m,1..n]的每个元素占用1个存储单元，对于数组元素A[i,j](1≤i≤m，1≤j≤n)，在按行存储方式下，其相对于数组空间首地址的偏移量为( )；在按列存储方式下，其相对于数组空间首地址的偏移量为(请作答此空)。

    A.j*(n-1)+i
    B.(j-1)*n+i-1
    C.j*(m-1)+i
    D.(j-1)*m+i-1

    答案：D
    解析：
    本题考查数据结构基础知识。数组A[1..m,1..n]的元素排列如下。

    解答该问题需先计算排列在a[i,j]之前的元素个数。
    按行方式存储下，元素a[i,j]之前有i-1行，每行n个元素，在第i行上a[i,j]之前有j-1个元素，因此，a[i,j]之前共有(i-1)*n+j-1个元素。
    在按列存储方式下，元素a[i,j]之前有i-1列，每列m个元素，在a[i,j]所在列(即第j列)，排在它之前的元素有i-1个，因此，a[i,j]之前共有(i-1)*m+i-1个元素。
    数组中指定元素的存储位置相对于数组空间首地址的偏移量等于k*d，其中k为排在该元素前的元素个数，d为每个元素占用的存储单元数。

  • 第18题：

    设数组a[0..n-1，0..m-1](n＞1，m＞1)中的元素以行为主序存放，每个元素占用1个存储单元，则数组元素a嘶](0＜i＜n,0＜j＜m)的存储位置相对于数组空间首地址的偏移量为( )。

    A.j*m+i
    B.i*m+j
    C.j*n+i
    D.i*n+j

    答案：B
    解析：
    本题考查程序语言基础知识。
    对于元素a[i,j]，按行存储方式下，其前面共有i行(行下标为0至行下标为i-1)、每行m个元素，合计i*m个元素。数组a中行下标为i的元素有a[i,0]、a[i,1]、…、a[i,j-1]、a[i,j]、…、a[i,m-1]，显然在该序列中，a[i,j]之前有j个元素，因此，数组元素a[i,j](0＜i＜n,0＜j＜m)之前共有i*m+j个元素，由于每个占用1个存储单元，故该元素的存储位置相对于数组空间首地址的偏移量为i*m+i。

  • 第19题：

    设数组a[1..n，1..m]（n>1，m>1）中的元素以行为主序存放，每个元素占用1个存储单元，则数组元素a[i，j]（1≤i≤n,i≤j≤m）相对于数组空间首地址的偏移量为（ ）。

    A.（i-1）*m+j-1
    B.（i-1）*n+j-1
    C.（j-1）*m+i-1
    D.（j-1）*n+i-1

    答案：A
    解析：
    数组 a[1..n，1..m] (n>1, m>1)如图所示：数组元素的存储地址=数组空间首地址+偏移量其中偏移量的计算方式为排列在所访问元素之前的元素个数乘以每个元素占用的存储单元数。对于元素a[i，j],在按行存储（以行为主序存放）方式下，该元素之前的元素个数为(i-1)*m+j-1。

  • 第20题：

    设数组a[1..n，1..m]（n>l，m>l）中的元素以行为主序存放，每个元素占用1个存储单元，则数组元素a[i，j]（1≤i≤n,i≤j≤m）相对于数组空间首地址的偏移量为（14）。

    A.（i-1）*m+j-1
    B.（i-1）*n+j-1
    C.（j-1）*m+i-1
    D.（j-1）*n+i-1

    答案：A
    解析：
    数组元素的存储地址=数组空间首地址+偏移量
    其中偏移量的计算方式为排列在所访问元素之前的元素个数乘以每个元素占用的存储单元数。
    对于元素a[i，j],在按行存储（以行为主序存放）方式下，该元素之前的元素个数为（i-1）*m+j-1。

  • 第21题：

    设数组a[0..n-1，0..m-1]（n>0，m>0）中的元素以列为主序存放，每个元素占用1个存储单元，则数组元素a[i，j]（0≤i≤n-1,0≤j≤m-1）相对于数组空间首地址的偏移量为（ ）。

    A.i*m+j
    B.（i-1）*n+j-1
    C.j*n+i
    D.（j-1）*n+i-1

    答案：C
    解析：
    数组a[0..n-1，0..m-1]（n>0，m>0）表示有n行m列，数组元素的存储地址=数组空间首地址+偏移量。其中偏移量的计算方式为排列在所访问元素之前的元素个数乘以每个元素占用的存储单元数。对于元素a[i，j],在按列存储（以列为主序存放）方式下，该元素之前有j列完整（因为首列编号为0）的元素，每一列n个元素，在第j列之前有i个元素（因为首行编号为0），所以偏移量为j*n+i。

  • 第22题：

    设S为C语言的语句，计算机执行下面算法时，算法的时间复杂度为（）。for（i=n-1；i>=0；i--）for（j=0；j

    • A、n2
    • B、O（nlgn）
    • C、O（n）
    • D、O（n2）

    正确答案:D

  • 第23题：

    单选题
    若二维数组arr［1..M，1..N］的首地址为base，数组元素按列存储且每个元素占用K个存储单元，则元素arr［i，j］在该数组空间的地址为（）。
    A

    base+（（i-1）*M+j-1）*K

    B

    base+（（i-1）*N+j-1）*K

    C

    base+（（j-1）*M+i-1）*K

    D

    base+（（j-1）*N+i-1）*K


    正确答案： A
    解析： 数据arr共M行N列，下标均从1开始。元素arr［i，j］在数据arr的第i行第j列，如果数组元素按列存储，则1～j-1列共有（j-1）*M个元素，a［i，j］之前共（j-1）*M+i-1个元素，元素arr［i，j］在该数组空间的地址为base+（（j-1）*M+i-1）*K。

相关内容