某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij,i=1或2,j=1,2,..n),两条装配线对应的工位完成同样的加工工作,但是所需要的时间可能不同(aij,i=1或2,j=1,2,... n)。汽车底盘开始到进入两条装配线的时间(e1,e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间(tij,i=1或2,j=2,n)。现在要以最快的时间完成一辆汽车的装配,求最优的装配路线。分析该问题,发现问题具有最优子结构。以L1为例,除了第一个工位
题目
(aij,i=1或2,j=1,2,... n)。汽车底盘开始到进入两条装配线的时间(e1,e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2,j=2,n)。现在要以最快的时间完成一辆汽车的装配,求最优的装配路线。
分析该问题,发现问题具有最优子结构。以L1为例,除了第一个工位之外,经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。

由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间,该问题具有重复子问题的性质,故采用迭代
方法求解。该问题采用的算法设计策略是(62) ,算法的时间复杂度为(63) 。
以下是一个装配调度实例,其最短的装配时间为(64) ,装配路线为(65) 。

B.23
C.20
D.26
相似考题
更多“某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij,i=1或2,j=1,2,..n),两条装配线对应的工位完成同样的加工工作,但是所需要的时间可能不同 ”相关问题
-
第1题:
阅读以下说明和图,填补流程图中的空缺。
【说明】
某汽车制造工厂有两条装配线。汽车装配过程如图10-6所示,即汽车底盘进入装配线,零件在多个工位装配,结束时汽车自动完成下线工作。
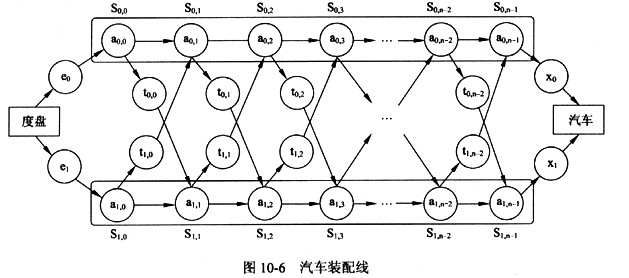
(1)e0和e1表示底盘分别进入装配线0和装配线1所需要的时间。
(2)每条装配线有n个工位,第一条装配线的工位为S0,0,S0,1,…,S0,n-0,第二条装配线的工位为S1,0,S1,1,…,S1,n-1。其中S0,k和S1,k(0≤k≤n-1)完成相同的任务,但所需时间可能不同。
(3)aij表示在工位Sij处的装配时间,其中i表示装配线(i=0或i=1),j表示工位号(0≤j≤n-1)。
(4)tij表示从Sij处装配完成后转移到另一条装配线下一个工位的时间。
(5)X0和X1表示装配结束后,汽车分别从装配线0和装配线1下线所需要的时间。
(6)在同一条装配线上,底盘从一个工位转移到其下一个工位的时间可以忽略不计。
图10-7所示的流程图描述了求最短装配时间的算法,该算法的输入为;
n: 表示装配线上的工位数;
e[i]: 表示e1和e2,i取值为0或1:
a[i][j]: 表示ai,j,i的取值为0或1,j的取值范围为0~n-1;
t[i][j]: 表示ti,j,i的取值为0或1,j的取值范围为0~n-1;
x[i]: 表示X0和X1,i取值为0或1。
算法的输出为:
fi:最短的装配时间;
li:获得最短装配时间的下线装配线号(0或者1)。
算法中使用的f[i][j]表示从开始点到Si,j处的最短装配时间。
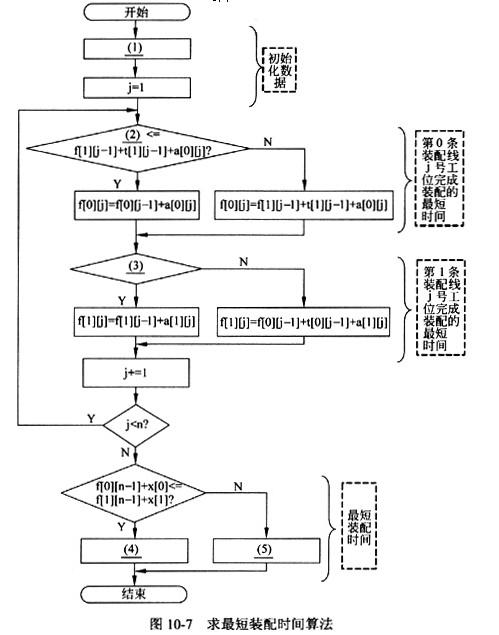 正确答案:(1)f[0][0]=e[0]+a[0][0] f[1][0]=e[1]+a[1][0] (2)f[0][j-1]+a[0][j] (3)f[j][j-1)+a[1][j]f[0][j-1)+t[0][j-1]+a[1][j] 或f[1][j-1)+a[1][j]=f[0][j-1]+t[0][j-1)+a[1][j] 或其等价形式 (4)fi=f[0][n-1]+x[0] li=0 (5)fi=f[1][n-1]+x[1] 1i=1
正确答案:(1)f[0][0]=e[0]+a[0][0] f[1][0]=e[1]+a[1][0] (2)f[0][j-1]+a[0][j] (3)f[j][j-1)+a[1][j]f[0][j-1)+t[0][j-1]+a[1][j] 或f[1][j-1)+a[1][j]=f[0][j-1]+t[0][j-1)+a[1][j] 或其等价形式 (4)fi=f[0][n-1]+x[0] li=0 (5)fi=f[1][n-1]+x[1] 1i=1
(1)f[0][0]=e[0]+a[0][0] f[1][0]=e[1]+a[1][0] (2)f[0][j-1]+a[0][j] (3)f[j][j-1)+a[1][j]f[0][j-1)+t[0][j-1]+a[1][j], 或f[1][j-1)+a[1][j]=f[0][j-1]+t[0][j-1)+a[1][j], 或其等价形式 (4)fi=f[0][n-1]+x[0] li=0 (5)fi=f[1][n-1]+x[1] 1i=1 解析:本题考查动态规划算法设计方法。
当问题具有两个特性,即最优子结构和重叠子问题时,可以考虑用动态规划求解问题。用动态规划求解问题具有四个步骤。
(1)刻画问题的最优子结构,描述问题的最优解包含子问题的最优解。对于本题来说,最短装配时间等于经过装配线。的第n个工位的最短装配时间加上x[0],或者等于经过装配线1的第n个工位的最短装配时间加上x[1],取哪条装配线取决于哪个值更小。而经过某个装配线0/1的第i个工位的最短装配时间又等于经过装配线0/1的第1-1个工位的最短装配时间,或者等于经过装配线I/0的第i-1个工位的最短装配时间加上从这个工位到装配线0/1的迁移时间,取决于哪个值更小。
(2)建立最优子结构的递归关系,这是非常关键的一步。对于本题来说,递归关系为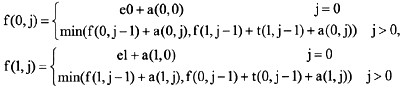
(3)根据递归关系求最优解的值。对于本题来说,最优解记录在fi中,fi= min(f(0,n-1)+x0,f(1,n-1)+x1):
(4)构造最优解。对于本题来说,只是求出最优解是从哪条装配线装配出来,并没有记录最优解。 -
第2题:
某汽车加工工厂有两条装配线L1和L2,每条装配线的工位数均为n(Sij,i=1或2,j= 1,2,...,n),两条装配线对应的工位完成同样的加工工作,但是所需要的时间可能不同(aij,i=1或2,j = 1,2,...,n)。汽车底盘开始到进入两条装配线的时间 (e1,e2) 以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间(tij,i=1或2,j =2,...n)。现在要以最快的时间完成一辆汽车的装配,求最优的装配路线。
分析该问题,发现问题具有最优子结构。以 L1为例,除了第一个工位之外,经过第j个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间如式(2)。

由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最短时间,该问题具有重复子问题的性质,故采用迭代方法求解。
该问题采用的算法设计策略是( ),算法的时间复杂度为( )
以下是一个装配调度实例,其最短的装配时间为( ),装配路线为( )

A.分治
B.动态规划
C.贪心
D.回溯
A. O(lgn)
B. O(n)
C. O(n2)
D. O(nlgn)
A.21
B.23
C.20
D.26
A.S11→S12→S13
B.S11→S22→S13
C.S21→S12→S23
D.S21→S22→S23
正确答案:B,B,A,B
-
第3题:
某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij,i=1或2,j=1,2,..n),两条装配线对应的工位完成同样的加工工作,但是所需要的时间可能不同
(aij,i=1或2,j=1,2,... n)。汽车底盘开始到进入两条装配线的时间(e1,e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2,j=2,n)。现在要以最快的时间完成一辆汽车的装配,求最优的装配路线。
分析该问题,发现问题具有最优子结构。以L1为例,除了第一个工位之外,经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。
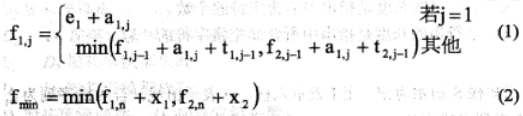
由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间,该问题具有重复子问题的性质,故采用迭代
方法求解。该问题采用的算法设计策略是(62) ,算法的时间复杂度为(63) 。
以下是一个装配调度实例,其最短的装配时间为(64) ,装配路线为(65) 。
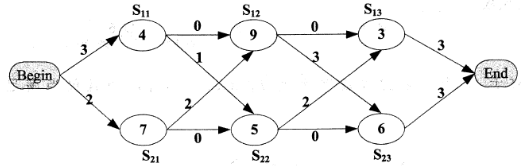 A.分治
A.分治
B.动态规划
C.贪心
D.回溯答案:B解析:动态规划算法与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。本题中的时间复杂度为O(n) 。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
求最短的装配时间与装配路线只需要将选项按照公式带入计算(将图上每条路径上的所有数字相加)可得最短路线为S11→S22→S13 ,时间为21。 -
第4题:
为什么要进行装配线的时间平衡?
正确答案: 因为,如果流水线不平衡将导致:
(1)浪费时间资源;
(2)忙闲不均,引起矛盾;
(3)浪费人力资源。
为此,必须进行装配线的时间平衡。 -
第5题:
以下是发动机装配线客户的有()。
- A、规划员
- B、维修工
- C、Careauditor
正确答案:C -
第6题:
以下是DOHC发动机装配线客户的有()
- A、规划员
- B、维修工
- C、凸轮轴机加工线
- D、以上都不是
正确答案:D -
第7题:
在实际使用的装配线中,各工位完全自动化常常是没有必要的。
正确答案:错误 -
第8题:
噬菌体T4的形态建成是一个井然有序的过程。从突变型推论,有几个装配线汇合后形成一个成熟的噬菌体。下面()答案是正确的?
- A、2个装配线
- B、4个装配线
- C、3个装配线
- D、5个装配线
正确答案:C -
第9题:
在装配线上,加工批量可能无限大。
正确答案:正确 -
第10题:
架空线路的同一横担上,L1、L2、L3、N、PE五条线的排列次序是面向负荷侧从左起依次为()
- A、L1、L2、L3、N、PE
- B、L1、N、L2、L3、PE
- C、L1、L2、N、L3、PE
- D、PE、N、L1、L2、L3
正确答案:B -
第11题:
单选题对于某装配流水线,在给定流水线的节拍后,求出装配线所需工序的工作地数量和用工人数的最小方案这是()。A节拍
B成组技术
C装配线平衡
D工艺的最优化
正确答案: D解析: 暂无解析 -
第12题:
单选题噬菌体T4的形态建成是一个井然有序的过程。从突变型推论,有几个装配线汇合后形成一个成熟的噬菌体。下面()答案是正确的?A2个装配线
B4个装配线
C3个装配线
D5个装配线
正确答案: B解析: 暂无解析 -
第13题:
阅读下列程序说明和C程序,将应填入(n)处的字句写在对应栏内。
[说明]
本程序将自然数1,2,……,N2(N=5)按蛇形方式逐个顺序存入N阶矩阵。令n=N-1,则矩阵中的每一元素可用aij标记,其中i,j(0≤i,j≤n)分别为其所在行的行号和所在列的列号。蛇形方式顺序存放的方法是从an0开始、到a0n为止,依次填入由1递增的自然数,交替地对每一斜列从左上角向右下角或从右下角向左上角排列。程序的输出为:
[程序]
include <stdio.h>
include <math.h>
define SIZE.10
int a[SIZE] [SIZE],k;
void write(int n) /*输出矩阵*/
{ int i,j;
for(i=0;i<=n;i+ +){
for(j=0; j<=nj j+ +)
printf("%4d",a[i][j]);
printf("\n");
}
}
void makeline(int row_start, int col_start, int row_end) /*完成矩阵一条斜线的整数填写*/
{ int i,j, sign;
sign=((1)> =0)? 1:-1;
for(i = row_start,j = col_start; (row_end-i) * sign>=0; i+=sign,j+=sign)
a[i][j]=(2);
}
void makeArray(int n) /*完成矩阵每条斜线的整数填写*/
{ int d;
for(d=1;d<=(3);d+ +)
if(d< =n+1)
if(d%2)
makeline((4));
else
makeline(n+1-d,0,n);
else
if(d%2)
makeline((5));
else
makeline(0,d-n-1,2*n-d+1);
}
void main()
{ int n, N=5;
k=1; n=N-1;
makeArray(n);
write(n);
}
正确答案:(1) row_end-row_start (2) k++ (3) 2* n+1 (4) nd-1n+1-d (5) 2*n-d+1n0
(1) row_end-row_start (2) k++ (3) 2* n+1 (4) n,d-1,n+1-d (5) 2*n-d+1,n,0 解析:本程序中二维数组a[][]用于存放矩阵元素,k表示当前应存放的元素(从1开始递增的某个自然数)。数据的填充按斜对角线进行,n+1阶矩阵的斜对角线有2*n+1条(包括两个单点an0、a0n。函数makeArray对斜对角线进行编号,从矩阵左下角开始依次为d=1,…,2*n,对于每条斜对角线,根据数据在其上的填充方式(左上角到右下角还是右下角到左上角)确定起点行号row_start、列号col_start以及终点行号 row_end,再调用函数makeline为这条线上填数。makeline函数根据row_end-row_start的正负判断数值填充方式。 -
第14题:
架空线路的同一横担上,L1(A)、L2(B)、L3(C)、N、PE五条线的排列次序是面向负荷侧从左起依次为()。A. L1、L2、L3、N、PE
B. L1、N、L2、L3、PE
C. L1、L2、N、L3、PE
D. PE、N、L1、L2、L3答案:B解析:架空线路的同一横担上,L1(A)、L2(B)、L3(C)、N、PE五条线的排列次序是面向负荷侧从左起依次为L1、N、L2、L3、PEP197:9.7.2动力、照明线在同一横担上架设时,导线相序排列顺序是:面向负荷从左侧起依次为L1、N、L2、L3、PE。 -
第15题:
某汽车加工工厂有两条装配线L1和L2;每条装配线的工位数均为n(Sij,i=1或2,j=1,2,..n),两条装配线对应的工位完成同样的加工工作,但是所需要的时间可能不同
(aij,i=1或2,j=1,2,... n)。汽车底盘开始到进入两条装配线的时间(e1,e2)以及装配后到结束的时间(X1X2)也可能不相同。从一个工位加工后流到下一个工位需要迁移时间
(tij,i=1或2,j=2,n)。现在要以最快的时间完成一辆汽车的装配,求最优的装配路线。
分析该问题,发现问题具有最优子结构。以L1为例,除了第一个工位之外,经过第j
个工位的最短时间包含了经过L1的第j-1个工位的最短时间或者经过L2的第j-1个工位的最
短时间,如式(1)。装配后到结束的最短时间包含离开L1的最短时间或者离开L2的最短时间
如式(2)。

由于在求解经过L1和L2的第j个工位的最短时间均包含了经过L1的第j-1个工位的最
短时间或者经过L2的第j-1个工位的最短时间,该问题具有重复子问题的性质,故采用迭代
方法求解。该问题采用的算法设计策略是(62) ,算法的时间复杂度为(63) 。
以下是一个装配调度实例,其最短的装配时间为(64) ,装配路线为(65) 。
 A.O(lgn)
A.O(lgn)
B.O(n)
C.O(n2)
D.O(nlgn)答案:B解析:动态规划算法与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。若用分治法来解这类问题,则分解得到的子问题数目太多,有些子问题被重复计算了很多次。如果能够保存已解决的子问题的答案,而在需要时再找出已求得的答案,这样就可以避免大量的重复计算,节省时间。可以用一个表来记录所有已解的子问题的答案。不管该子问题以后是否被用到,只要它被计算过,就将其结果填入表中。这就是动态规划法的基本思路。本题中的时间复杂度为O(n) 。
贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择,即贪心选择来达到。这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
回溯算法实际上一个类似枚举的搜索尝试过程,主要是在搜索尝试过程中寻找问题的解,当发现已不满足求解条件时,就“回溯”返回,尝试别的路径。回溯法是一种选优搜索法,按选优条件向前搜索,以达到目标。但当探索到某一步时,发现原先选择并不优或达不到目标,就退回一步重新选择,这种走不通就退回再走的技术为回溯法,而满足回溯条件的某个状态的点称为“回溯点”。
求最短的装配时间与装配路线只需要将选项按照公式带入计算(将图上每条路径上的所有数字相加)可得最短路线为S11→S22→S13 ,时间为21。 -
第16题:
TN-S配电系统的架空线路,面向负荷侧时的导线排列顺序为()。
- A、L1、N、L2、L3、PE;
- B、L3、L2、L1、N、PE;
- C、L2、L3、N、L1、PE;
- D、L2、L3、PE、L1、N;
正确答案:A -
第17题:
以下是发动机装配线客户的有()
- A、规划员
- B、维修工
- C、凸轮轴机加工线
- D、以上都不是
正确答案:D -
第18题:
DOHC发动机装配线(装配A线)上有几个自动检测工位?()
- A、1个
- B、2个
- C、3个
- D、4个以上
正确答案:B -
第19题:
自动装配线的基本特征是在装配工位上,将各种装配件装配到装配基础件上去,完成一个部件或一个产品的装配
正确答案:正确 -
第20题:
对于某装配流水线,在给定流水线的节拍后,求出装配线所需工序的工作地数量和用工人数的最小方案这是()。
- A、节拍
- B、成组技术
- C、装配线平衡
- D、工艺的最优化
正确答案:C -
第21题:
在装配线上,转运批量可能为1。
正确答案:正确 -
第22题:
装配线实际上运行时间与规定运行时间的比率()。
- A、装配线开动率
- B、工时定额
- C、生产节拍
- D、工位密度
正确答案:A -
第23题:
判断题在装配线上,加工批量可能无限大。A对
B错
正确答案: 对解析: 暂无解析
