某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为 （请作答此空） ，若问题的规模增加了16倍，则运行时间增加 （ ） 倍。A.O(n) B.O(nlgn) C.O(n2) D.O(n2lgn)

题目
某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为 （请作答此空） ，若问题的规模增加了16倍，则运行时间增加 （ ） 倍。

A.O(n)
B.O(nlgn)
C.O(n2)
D.O(n2lgn)
相似考题

1.当问题的规模n趋向无穷大时,算法执行时间T(n)的数量级被称为算法的时间复杂度。()此题为判断题(对，错)。

2.设某算法的计算时间可用递推关系式T(n)=2T(n/2)+n表示，则该算法的时间复杂度为(59)。A．O(1gn)B．O(nlgn)C．O(n)D．O(n2)

3.● 某算法的时间复杂度表达式为 T(n)=an2+bnlgn+cn+d，其中，n为问题的规模，a、b、c和d为常数，用O表示其渐近时间复杂度为 （63）。（63）A. O(n2) B. O (n) C. O (n1gn) D. O (1)

4.若一个算法中的语句频度之和为T(n)=3720n＋4nlogn,则算法的时间复杂度为 O(n)。()此题为判断题(对，错)。

更多“某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为 （请作答此空） ，若问题的规模增加了16倍，则运行时间增加 （ ） 倍。”相关问题

  • 第1题：

    某算法的时间复杂度可用递归式[*],表示，若用[*]表示该算法的渐进时间复杂度的紧致界，则正确的是(62)。

    A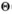．(nlg2n)

    B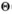．(nlgn)

    C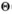．(n2)

    D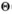．(n3)


    正确答案：A
    解析：本题利用递归树方法求解。得到的递归树如下图所示：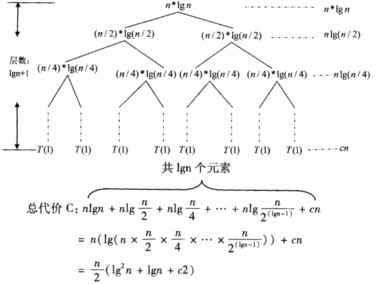

     由于C属于O(nlg2n)且C属于Ω(nlg2n)，所以总的时间复杂度为A。

  • 第2题：

    假设某算法的计算时间可用递推关系式T(n)=2T(n/2)+n，T(1)=1表示，则该算法的时间复杂度为()

    A.O(logn)

    B.O(n*logn)

    C.O(n)

    D.O(n^2)


    正确答案：B

  • 第3题：

    A算法的时间复杂度为O(n^3),B算法的时间复杂度为O(2n),则说明()。

    A对于任何的数据量，A算法的时间开销都比B算法小

    B随着问题规模n的增大，A算法比B算法有效

    C随着问题规模n的增大，B算法比A算法有效

    D对于任何数据量，B算法的时间开销都比A算法小


    参考答案：B

  • 第4题：

    ● 若某算法在问题规模为 n 时，其基本操作的重复次数可由下式表示，则该算法的时间复杂度为 （64） 。

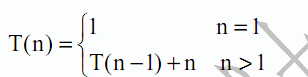
    （64）A. O(n) B. O(n2) C. O(logn) D. O(nlogn)


    正确答案：B

  • 第5题：

    计算N!的递归算法如下，求解该算法的时间复杂度时，只考虑相乘操作，则算法的计算时间T(n)的递推关系式为(55)；对应时间复杂度为(56)。

    int Factorial (int n)

    {//计算n!

    if(n＜=1)return 1;

    else return n * Factorial(n-1);

    }

    (62)

    A．T(n)=T(n-1)+1

    B．T(n)=T(n-1)

    C．T(n)=2T(n-1)+1

    D．T(n)=2T(n-1)-1


    正确答案：A

  • 第6题：

    设求解某问题的递归算法如下：

    F(int n){

    if n=1 {

    Move(1)

    }else{

    F(n-1)；

    Move(n)；

    F(n-1)；

    }

    }

    求解该算法的计算时间时，仅考虑算法Move所做的计算为主要计算，且Move为常数级算法。则算法F的计算时间T(n)的递推关系式为(9)；设算法Move的计算时间为k，当 n=4时，算法F的计算时间为(10)。

    A．T(n)=T(n-1)+1

    B．T(n)=2T(n-1)

    C．T(n)=2T(n-1)+1

    D．T(n)=2T(n+1)+1


    正确答案：C

  • 第7题：

    在某个算法时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为（ ），若问题的规模增加了16倍，则运行时间增加（ ）倍。

    A.Θ(n) B.Θ(nlgn) C.Θ(n2) D.Θ(n2lgn) A.16 B.64 C.256 D.1024


    正确答案：C,C

  • 第8题：

    某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为（62），若问题的规模增加了16倍，则运行时间增加（63）倍。

    A.16
    B.64
    C.256
    D.1024

    答案：C
    解析：
    对于递归式，假设T(1)=1，则：
    T(n)=T(n-1)+n
    =T(n-2)+n-1+n
    =T(n-3)+n-2+n-1+n
    =1+2+…+n-1+n
    =n(n+1)/2
    可见，时间复杂度为O(n2)。若问题的规模增加了16倍，则运行时间增加了162=256倍。

  • 第9题：

    已知算法A的运行时间函数为T（n）=8T（n/2）+n2，其中n表示问题的规模，另已知算法B的运行时间函数为T（n）=XT（n/4）+n2，其中n表示问题的规模。对充分大的n，若要算法B比算法A快，则X的最大值为（ ）。

    A.15
    B.17
    C.63
    D.65

    答案：C
    解析：
    本题需要用到特定形式的递归式分析法：



    在本题中，a=8,b=2，故符合（1）的情况。

    时间复杂度为：O（n3）。

    a=16,b=4

  • 第10题：

    某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为（62），若问题的规模增加了16倍，则运行时间增加（63）倍。

    A.O(n)
    B.O(nlgn)
    C.O(n2)
    D.O(n2lgn)

    答案：C
    解析：
    对于递归式，假设T(1)=1，则：
    T(n)=T(n-1)+n
    =T(n-2)+n-1+n
    =T(n-3)+n-2+n-1+n
    =1+2+…+n-1+n
    =n(n+1)/2
    可见，时间复杂度为O(n2)。若问题的规模增加了16倍，则运行时间增加了162=256倍。

  • 第11题：

    设待处理问题的规模为n，若一个算法的时间复杂度为一个常数，则表示成数量级的形式为（），若为n*log25n，则表示成数量级的形式为（）。


    正确答案:Ο（1）；Ο（nlog2n）

  • 第12题：

    填空题
    设待处理问题的规模为n，若一个算法的时间复杂度为一个常数，则表示成数量级的形式为（），若为n*log25n，则表示成数量级的形式为（）。

    正确答案： Ο（1）,Ο（nlog2n）
    解析： 暂无解析

  • 第13题：

    某算法的时间复杂度表达式为T(n)=an2+bnlgn+cn+d，其中，n为问题的规模，a、b、c和d为常数，用O表示其渐近时间复杂度为( )。

    A．(n2)

    B．O(n)

    C．O(nlgn)

    D．O(1)


    正确答案：A
    解析：时间复杂度是度量算法执行的时问长短。根据表达式T(n)=an2+bnlgn+cn+d可知当n无限大时，T(n)=an2，故时间复杂度为O(n2)

  • 第14题：

    某算法的时间代价递推关系为T(n)=2T(n/2)+n，T(1)=1，则该算法的时间复杂度为______。

    A．O(n)

    B．

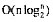
    C．O(n2)

    D．O(1)


    正确答案：B
    解析：由时间代价严格推出时间复杂度比较复杂，对于这种题，可用特例验证，不过需要注意的是特例不能取太少，至少n取到5，这样规律基本就可以确定了。
      T(1)=1
      T(2)=2T(1)+2=4
      T(3)=2T(1)+3=5
      T(4)=2T(2)+4=12
      T(5)=2T(2)+5=13
      很容易排除D选项，其递增速率介于O(n)和O(nsup>2</sup>)之间，故选B。

  • 第15题：

    ● 设某算法的计算时间表示为递推关系式T(n)= T(n-1) + n (n>0) 及T(0)=1，则该算法的时间复杂度为 （65） 。


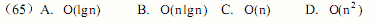    正确答案：D

  • 第16题：

    若n表示问题的规模、O(f(n))表示算法的时间复杂度随n变化的增长趋势，则算法时间复杂度最小的是(59)。

    A．O(n2)

    B．O(n)

    C．O(logn)

    D．O(nlogn)


    正确答案：C
    解析：本题考查的是算法消耗的时间度量。一般情况下，一个算法中基本操作重复执行的次数是问题规模n的某个函数f(n)，算法的时间量度记作T(n)=O(f(n))，它表示随问题n的增大，算法执行时间的增长率和　f(n)的增长率相同，称做算法的渐进时间复杂度，简称时间复杂度。显然，在O(n2)、O(n)、　O(logn)和O(nlogn)中，复杂度最小的是O(logn)。

  • 第17题：

    设某算法的计算时间表示为递推关系式T(n)＝T(n-1)+n(n＞O)及T(0)＝1，则该算法的时间复杂度为(65)。

    A．O(lgn)

    B．O (nlgn)

    C．O(n)

    D．O(n2)


    正确答案：D
    解析：本题考查算法设计基础知识。根据题目中给出的递推关系：T(n)＝T(n-1)+n＝T(n-2)+n-1+n＝…＝T(0)+1+2+…+n-1+n＝1+n(n+1)/2

  • 第18题：

    设某算法的计算时间可用递推关系式T(n)=2T(n/2)+n表示，则该算法的时间复杂度为(1)。

    A．O(lgn)

    B．O(nlgn)

    C．O(n)

    D．O(n2)


    正确答案：B
    解析：运用数学递推公式，可以推算出数量级O(nlgn)。

  • 第19题：

    某个算法的时间复杂度递归式T(n)=T(n-1)+n，其中n为问题的规模，则该算法的渐进时间复杂度为 （ ） ，若问题的规模增加了16倍，则运行时间增加 （请作答此空） 倍。

    A.16
    B.64
    C.256
    D.1024

    答案：C
    解析：
    对于递归式，假设T(1)=1，则：
    T(n)=T(n-1)+n
    =T(n-2)+n-1+n
    =T(n-3)+n-2+n-1+n
    =1+2+…+n-1+n
    =n(n+1)/2
    可见，时间复杂度为O(n2)。若问题的规模增加了16倍，则运行时间增加了162=256倍。

  • 第20题：

    已知算法A的运行时间函数为T（n）=8T（n/2）+n2，其中n表示问题的规模，则该算法的时间复杂度为（ ）

    A.θ（n）
    B.θ（nlgn）
    C.θ（n2）
    D.θ（n3）

    答案：D
    解析：
    本题需要用到特定形式的递归式分析法：
    在本题中，a=8,b=2，故符合（1）的情况。时间复杂度为：O（n3）。a=16,b=4

  • 第21题：

    设某算法的计算时间表示为递推关系式T（n）＝T（n-1）+n（n＞O）及T（0）＝1，则该算法的时间复杂度为（ ）。

    A.O（lgn）
    B.O（nlgn）
    C.O（n）
    D.O（n^2）

    答案：D
    解析：
    本题考查算法设计基础知识。根据题目中给出的递推关系：T（n）＝T（n-1）+n＝T（n-2）+n-1+n＝…＝T（0）+1+2+…+n-1+n＝1+n（n+1）/2

  • 第22题：

    时间复杂度记为：T（n）=O（f（n））；其中n是（）。

    • A、函数
    • B、问题的规模
    • C、渐近符号
    • D、规模的函数

    正确答案:B

  • 第23题：

    单选题
    时间复杂度记为：T（n）=O（f（n））；其中n是（）。
    A

    函数

    B

    问题的规模

    C

    渐近符号

    D

    规模的函数


    正确答案： C
    解析： 暂无解析

相关内容