菲波那契(Fibonacci)数列定义为 f(1)=1，f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出，n>1时，有向量的递推关系式： (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵（）。从而，f(n+1),f(n)=(f(2),f(1))*（65）.A.An-1 B.An C. An+1 D. An+2

题目
菲波那契(Fibonacci)数列定义为
f(1)=1，f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
据此可以导出，n>1时，有向量的递推关系式：
(f(n+1),f(n))=f(f(n),f(n-1))A
其中A是2*2矩阵（）。从而，f(n+1),f(n)=(f(2),f(1))*（65）.

A.An-1
B.An
C. An+1
D. An+2
相似考题

1.函数fib1、fib2求得菲波那契数列第n项(n＞40)的速度并不相同，清指出速度慢的函数名，并简要说明原因。

2.大多数植物的花瓣数都符合斐波那契数列。()此题为判断题(对，错)。

3.下面的程序是求菲波那契(Fibonacci)数列的前10项。已知该数列的前两项都为1，即F(1)=1，F(2)=1；而后面各项满足： F(n)=F(n-1)+F(n-2)。请在程序的每条横线处填写一条语句，使程序的功能完整。注意：请勿改动main()主方法和其他已有的语句内容，仅在横线处填入适当的语句。public class Fibonacci{public static void main(String args[]){System.out.printtn("Fibonacci is"+" "+"_______________________);}static long fib(int n){if(______________)return 1;elsereturn _________________}}

4.1、1、2、3、5、8是斐波那契额数列。()此题为判断题(对，错)。

参考答案和解析
答案：A
解析：
本题考查数学应用的基础知识。
若矩阵A选取（64）中的D，则
（f（n），f（n-1））A=（f（n）+f（n-1），f（n））=（f（n+1），f（n））
由递推关系（f（n+1），f（n））=（f（n），f（n-1））A，
得到（f（n+1），f（n））：（f（n），f（n-1））A=f（n-1），f（n-2））A2=（f（n-2），f（n-3））A3=...
=（f（2），f（1）An-1=（1,1）An-1
这就给出了计算菲波那契数列的另一种算式。
更多“菲波那契(Fibonacci)数列定义为 ”相关问题

  • 第1题：

    ● 斐波那契(Fibonacci)数列可以递归地定义为：

    ?

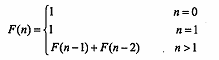
    用递归算法求解F(5)时需要执行 （63） 次“+”运算，该方法采用的算法策略是 （64） 。

    （63）

    A. 5

    B. 6

    C. 7

    D. 8

    （64）

    A. 动态规划

    B. 分治

    C. 回溯

    D. 分支限界


    正确答案：C,B

  • 第2题：

    菲波那契(Fibonacci)数列定义为 f(1)=1，f(2)=1,n>2时f(n)=f(n-1)+f(n-2) 据此可以导出，n>1时，有向量的递推关系式： (f(n+1),f(n))=f(f(n),f(n-1))A 其中A是2*2矩阵（ ）。从而，(f(n+1),f(n)=(f(2),f(1))*（ ）

    A.B.C.D.A.An-1B.AnC.An+1D.An+2


    正确答案：D,A

  • 第3题：

    阅读说明和流程图，填补流程图中的空缺（1）?（5），将答案填入答题纸对应栏内。【说明】本流程图用于计算菲波那契数列{a1=1，a2=1，…,an=an-1+an-2!n=3,4,…}的前n项（n>=2) 之和S。例如，菲波那契数列前6项之和为20。计算过程中，当前项之前的两项分别动态地保存在变量A和B中。【流程图】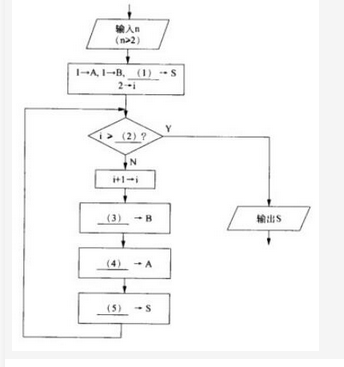


    答案：
    解析：
    （1）2或A+B（2）n（3）A+B（4）B-A（5）S+B
    【解析】

    菲波那契数列的特点是首2项都是1，从第3项开始，每一项都是前两项之和。该数列的前几项为1，1，2, 3，5，8，…。在流程图中，送初始值1—A，2—B后，显然前2项的和S应等于2,所以（1）处应填2 (或A+B)。此时2→i (i表示动态的项编号），说明已经计算出前2项之和。接着判断循环的结束条件。显然当i=n时表示已经计算出前n项之和，循环可以结束了。因此（2）处填n。判断框中用“>”或“≥”的效果是一样的，因为随着i的逐步增1，只要有i=n结束条件就不会遇到i>n的情况。不过编程的习惯使循环结束条件扩大些，以防止逻辑出错时继续循环。接下来i+1→i表示数列当前项的编号增1，继续往下计算。原来的前两项值（分别在变量A和B中）将变更成新的前两项再放到变量A和B中。

    首先可以用A+B—B实现（原A) + (原B)—(新B)，因此（3）处填A+B。为了填新A值（原来的B值)，不能用B—A，因为变量B的内容已经改变为（原A) + (原B)，而B-A正是（（原A) + (原B))-(原A)=(原B)，因此可以用B-A—A来实现新A的赋值。这样，（4）处填B-A。最后应是前n项和值的累加（比原来的S值增加了新B值)，所以（5）处应填S+B。填完各个空后，最好再用具体的数值来模拟流程图走几个循环检查所填的结果（这是防止逻辑上出错的好办法）。

  • 第4题：


    A.等比数列
    B.斐波那契数列
    C.柱式比例
    D.高斯比例

    答案：B
    解析：

  • 第5题：

    自然界中存在丰富的斐波那契数列，斐波那契数列来源于一个古老的数学问题，是由12世纪意大利数学家斐波那契在其书中所产生的。斐波那契数列和黄金分割的关系是？（）

    • A、黄金比例是斐波那契数列中的一项
    • B、斐波那契数列相邻两项的比例逐渐逼近黄金比例
    • C、黄金分割是指用斐波那契数列对一个量进行分割
    • D、黄金比例是斐波那契数列的别名

    正确答案:B

  • 第6题：

    数据结构里，斐波那契数列的递归实现方法，就会使用到栈。


    正确答案:正确

  • 第7题：

    以下属于二阶递推公式的是（）。

    • A、圆的面积公式
    • B、等差数列
    • C、等比数列
    • D、斐波那契数列

    正确答案:D

  • 第8题：

    斐波那契（Fibonacci）的斐波那契数列是在（）年提出于他的著作《算盘书》中。

    • A、1202
    • B、1217
    • C、1228
    • D、1233

    正确答案:C

  • 第9题：

    斐波那契在《计算之书》中，为表达庞大数字的表达方法来引出（）的概念。

    • A、数列
    • B、幂
    • C、函数
    • D、对数

    正确答案:B

  • 第10题：

    单选题
    被称为黄金分割数列的是（）。
    A

    格伦布数列

    B

    卡迈克尔数

    C

    毕达哥拉斯素数

    D

    斐波那契数列


    正确答案： D
    解析： 暂无解析

  • 第11题：

    填空题
    斐波那契数列的第一项是（），第七项是（）。

    正确答案： 1,13
    解析： 暂无解析

  • 第12题：

    单选题
    斐波那契（Fibonacci）的斐波那契数列是在（）年提出于他的著作《算盘书》中。
    A

    1202

    B

    1217

    C

    1228

    D

    1233


    正确答案： A
    解析： 暂无解析

  • 第13题：

    斐波那契(Fibonacci)数列可以递归地定义为：

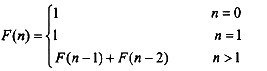
    用递归算法求解F(5)时需要执行(63)次“+”运算，该方法采用的算法策略是(64)。

    A．5

    B．6

    C．7

    D．8


    正确答案：C

  • 第14题：

    菲波那契(Fibonacci)数列定义为
    f(1)=1，f(2)=1,n>2时f(n)=f(n-1)+f(n-2)
    据此可以导出，n>1时，有向量的递推关系式：
    (f(n+1),f(n))=f(f(n),f(n-1))A
    其中A是2*2矩阵（64）。从而，f(n+1),f(n)=(f(2),f(1))*（65）.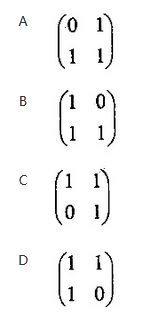


    答案：D
    解析：
    本题考查数学应用的基础知识。
    若矩阵A选取（64）中的D，则
    （f（n），f（n-1））A=（f（n）+f（n-1），f（n））=（f（n+1），f（n））
    由递推关系（f（n+1），f（n））=（f（n），f（n-1））A，
    得到（f（n+1），f（n））：（f（n），f（n-1））A=f（n-1），f（n-2））A2=（f（n-2），f（n-3））A3=...
    =（f（2），f（1）An-1=（1,1）An-1
    这就给出了计算菲波那契数列的另一种算式。

  • 第15题：

    中世纪数学家比萨的莱奥纳多发现了斐波那契数列，它是这样一组数列：1、1、2、3、5······即后一数字为前面两个数字之和。那么，数列和树木的成长有什么关联呢？由于新生的枝条，往往需要一段“休息”时间，供自身生长，而后才能萌发新枝。所以，一株树苗在一段间隔，例如一年，以后长出一条新枝；第二年新枝“休息”，老枝依旧萌发；此后，老枝与“休息”过一年的枝同时萌发，当年生的新枝则次年“休息”。这样，一株树木各个年份的枝桠数，便构成斐波那契数列。这段文字意在说明：

    A.斐波那契数列表现为树本的年轮增长
    B.斐波那契数列在自然界中无处不在
    C.斐波那契数列在自然中的应用
    D.斐波那契数列表明植物在大自然中长期造应和进化

    答案：C
    解析：
    文段首先表述了什么是斐波那契数列，接着提出问题，就是该数列和树木生长的的关系，然后对这一问题做出了回答。A项未提及年轮；B项无处不在过于绝对；D项植物扩大概念和无中生有，文段是围绕树木来讲述的。因此，该题选择C项。

  • 第16题：


    A.等比数列、斐波那契数列
    B.黄金分割、斐波那契数列
    C.等比数列、黄金分割
    D.调和数列、黄金分割

    答案：B
    解析：
    勒·柯布西耶提出的模距图所列数字之间，存在黄金分割、斐波那契数列。斐波那契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、…在数学上，斐波那契数列以如下递归的方法定义：F0=0，F1=1，Fn=F(n-1)+F(n-2)(n＞=2，n∈N*)。在现代物理、准晶体结构、化学等领域，斐波那契数列都有直接的应用。

  • 第17题：

    “0，1，1，2，3，5，8，13，21”这个著名数列名为？（）

    • A、大衍数列
    • B、斐波那契数列
    • C、陈景润数列
    • D、卢卡斯数列

    正确答案:B

  • 第18题：

    如果要推广斐波那契数列，最应该关注的是数列的（）。

    • A、表达公式
    • B、递推关系
    • C、第一项
    • D、第二项

    正确答案:B

  • 第19题：

    斐波那契数列的第一项是（），第七项是（）。


    正确答案:1；13

  • 第20题：

    被称为黄金分割数列的是（）。

    • A、格伦布数列
    • B、卡迈克尔数
    • C、毕达哥拉斯素数
    • D、斐波那契数列

    正确答案:D

  • 第21题：

    单选题
    自然界中存在丰富的斐波那契数列，斐波那契数列来源于一个古老的数学问题，是由12世纪意大利数学家斐波那契在其书中所产生的。斐波那契数列和黄金分割的关系是？（）
    A

    黄金比例是斐波那契数列中的一项

    B

    斐波那契数列相邻两项的比例逐渐逼近黄金比例

    C

    黄金分割是指用斐波那契数列对一个量进行分割

    D

    黄金比例是斐波那契数列的别名


    正确答案： D
    解析： 暂无解析

  • 第22题：

    单选题
    以下属于二阶递推公式的是（）。
    A

    圆的面积公式

    B

    等差数列

    C

    等比数列

    D

    斐波那契数列


    正确答案： B
    解析： 暂无解析

  • 第23题：

    单选题
    斐波那契数列取自哪个国家的数学家（）
    A

    法国

    B

    英国

    C

    意大利

    D

    德国


    正确答案： A
    解析： 暂无解析

相关内容