社会福利服务政策的基本内容包括()。A.满足社会成员基本生活需求的服务体系B.满足社会共同生活需要的服务体系C.针对特殊困难者的社会福利服务体系D.针对家庭成员提供的援助服务E.针对亲友的援助服务
题目
社会福利服务政策的基本内容包括()。
A.满足社会成员基本生活需求的服务体系
B.满足社会共同生活需要的服务体系
C.针对特殊困难者的社会福利服务体系
D.针对家庭成员提供的援助服务
E.针对亲友的援助服务
相似考题
更多“社会福利服务政策的基本内容包括()。 ”相关问题
-
第1题:
社会政策具有社会性的特征,其内容包括()。A:社会管理
B:社会性服务
C:社会福利
D:社会性目标
E:社会性价值答案:D,E解析:社会政策具有社会性的特征,其内容包括社会性目标、社会性价值。 -
第2题:
简述社会福利函数的基本内容。答案:解析:社会福利函数是社会所有人的效用水平的函数,在两个人的社会中,社会福利函数可以表示为W=(UA,UB),其中,W表示社会福利,%、UB表示两个人的效用水平指标。上式表明社会福利取决于UA、UB的大小,利用该关系可以得到社会无差异盐线,如图9-3所示,横轴和纵轴分别代表UA、UB,和消费者的无差异衄线一样,社会无差异曲线也具有无限条,表示社会福利水平的高低。 在图9-3中有三条社会无差异曲线W1、W2、W3,这种曲线不计算社会福利的大小,但能比较社会福利的高低,位置越高的社会无差异曲线代表的社会福利越大。uu’是总效用可能曲线,它类似于消费者行为理论中的收入约束线。同样的道理,最大的社会福利只会出现在总效用可能线uu’和社会无差异线W2的切点上,这一点叫作“限制条件下的最大满足点”。这是能导致最大社会福利的生产、交换和分配的唯一一点。之所以叫作限制条件下的最大满足点,是因为最大社会福利并不允许为任何可能值,而要受到既定的生产资源、生产技术条件等的限制,uu’曲线和W1相交于A点和A’点,这些点所代表的社会福利都低于W2,而uu’和W3没有交点,说明在现有的条件下无法达到W3的社会福利水平。 社会福利函数由美国经济学家肯尼斯·阿罗提出的。阿罗认为,社会福利函数必须具有人们可以普遍接受的性质,而这样的福利函数在逻辑上根本就不可能存在。他指出,一个能被人们普遍接受的社会福利函数必须具备如下性质:①与个人的偏好一样,社会的偏好必须能够用无差异曲线或直接用偏好来排定其顺序,而且排列的原则是始终一致的;②如果情况A是社会偏好的,而B不是,或者说社会把对A的偏好排在B之上,当一个人或更多的人将其个人对B的偏好排在比A更高的位置时,社会必须仍保持对A更高的位置时,社会必须仍保持对A的偏好胜于B的判断;③假设某一个人对A的偏好胜于B,对B的偏好胜于C,而且A又是社会的最大偏好。如果这个人改变了其偏好排列,认为.4胜于C、C胜于B,那么不管社会对C和B的偏好是否变化,A仍旧是社会的最大偏好;④对任意两种情况A和B,如果所有个人对.的偏好都胜于B,那么社会对B的偏好就不可能胜于A;⑤社会对A的偏好胜于B,不能只是因为有一个人对A的偏好胜于B。但阿罗又认为,不可能有任何一个社会在同时满足上述五个性质的情况下排出各种情况的顺序,即这样的社会福利函数是不存在的。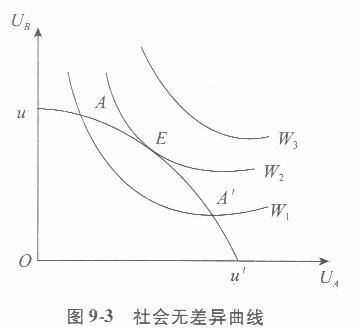
-
第3题:
社会行政的要件除了社会福利资源之外,还包括
A.社会政策
B.社会行政人员
C.社会服务机构
D.社会服务人员
社会政策;社会行政人员;社会服务机构;社会服务人员 -
第4题:
社会行政要件包括( )A.社会政策
B.社会福利资源
C.社会服务机构
D.社会行政人员
E.社会服务人员答案:A,B,C,D,E解析: -
第5题:
社会福利是社会保障的最基本内容。
错误
