试用代数法将如下逻辑函数式化简成最简与或式。(1) Y1=A－B－C＋(A＋B＋C—————)＋A－B－C－D(2)Y2=ABCD＋ABCD——＋AB——CD(3) Y3=ABC(AB＋C－(BC＋AC))

题目
试用代数法将如下逻辑函数式化简成最简与或式。(1) Y1=A－B－C＋(A＋B＋C—————)＋A－B－C－D(2)Y2=ABCD＋ABCD——＋AB——CD(3) Y3=ABC(AB＋C－(BC＋AC))

相似考题

1.用PL实现逻辑函数时，首先将逻辑函数化简为最简与或式()

2.代数式，|e2×A＋lgy13+sin y2|对应的Visual Basic表达式是 ______。A．Abs(e^2*a+Log(y1^3)+Sin(y2))B．Abs(Exp(2)*a+Log(y1^3)／Log(10)+Sin(y2))C．Abs(e^2*a+lg(y1^3)+Sin(y2))D．Abs(Exp(2)*a+Log(y1^3)+Sin(y2))

3.画出如下逻辑函数式的逻辑电路图。答案：25.写出表题 2-25的与或逻辑函数式。Y=A-B-C+ABC+AB-C-+AB-C

4.已知组合逻辑函数Y=ABC＋ABD＋AC'D＋C'D'＋AB'C＋A'CD',试用卡诺图化简法化为最简与或表达式

更多“试用代数法将如下逻辑函数式化简成最简与或式。(1) Y1=A－B－C＋(A＋B＋C—————)＋A－B－C－D(2)Y2=ABCD＋ABCD——＋AB——CD(3) Y3=ABC(AB＋C－(BC＋AC)) ”相关问题

  • 第1题：

    试用卡诺图化简如下具有任意项的逻辑函数式。


    答案：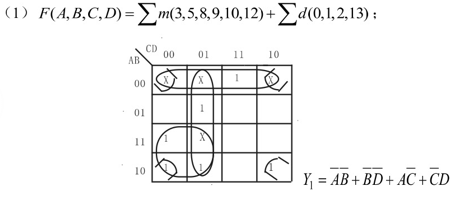

  • 第2题：

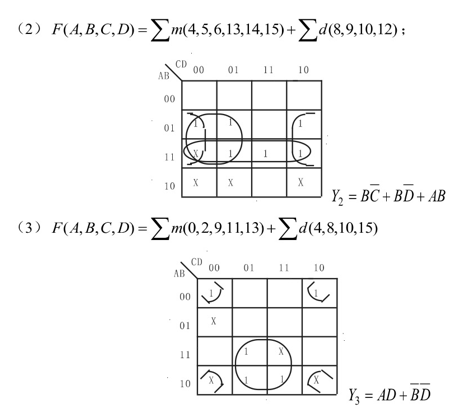
    试用 卡诺图化简如下逻辑函数式。


    答案：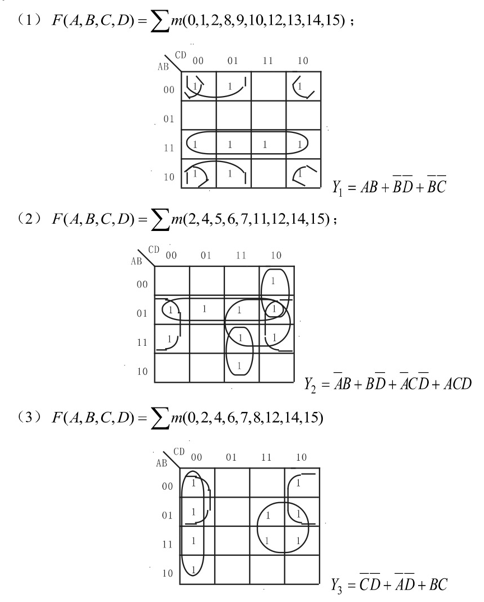

  • 第3题：

    试用卡诺图化简如下逻辑函数式。(1) Y1=ABC＋ABC－＋B－(2) Y2=A＋AB－C＋AB(3) Y3=AC－＋AB－＋AB(4) Y4=AB－C－＋AC－＋C


    答案：(1) Y1=ABC+ABC-+B-(2) Y2=A+AB-C+AB(3) Y3=AC-+AB-+AB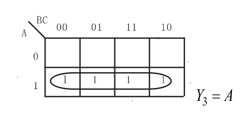(4) Y4=AB-C-+AC-+C

  • 第4题：

    2 .使用与门、或门实现如下的逻辑函数式。(1) Y1= ABC＋ D (2) Y2= A(CD＋ B) (3) Y3=AB＋C


    答案：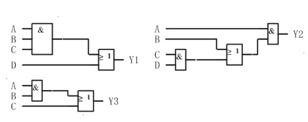

  • 第5题：

    用ROM实现如下逻辑函数(采用74LS138作为地址译码器)Y1(A, B, C)=∑m (3,6,7)Y2(A, B, C)=∑m (0,1,4,5,6)Y3(A,B, C)=∑m (2,3,4)Y4(A, B, C)=∑m (2,3,4,7)


    答案：

  • 第6题：

    逻辑函数式P（A，B，C）＝Σm（3，5，6，7）化为最简与或式形式为（　　）。

    A． BC＋AC
    B． C＋AB
    C． B＋A
    D． BC＋AC＋AB

    答案：D
    解析：
    画出该函数式的卡诺图，如下图所示。画包围圈合并最小项后得到最简与或表达式为：Y＝BC＋AC＋AB。

  • 第7题：

    仔细阅读下面程序，请给出运行结果（ ）。#include#includeint f1（int x）{return x*x；}int f2（int x）{return x*x*x；}main（ ）{int x=3,y1,y2,y3,y4；int（*f）（ ）；f=f1；y1=（*f）（x）；y2=f1（x）；f=f2；y3=f（x）；y4=f2（x）；printf（“y1=%d，y2=%d，y3=%d，y4=%d\n”，y1，y2，y3，y4）；}

    A.y1=9,y2=9,y3=27,y4=27
    B.y1=3,y2=9,y3=27,y4=9
    C.y1=3,y2=3,y3=9,y4=9
    D.y1=3,y2=9,y3=9,y4=27

    答案：A
    解析：
    题中y2和y4是直接函数调用，毫无疑问是9和27，关键在于f=f1是将函数指针f指向了函数f1，因此y1=（*f）（x）本质是调用了函数f1，其结果与直接调用y2=f1（x）相同，y3同理。

  • 第8题：

    逻辑函数Y=ABC+AC+BC的最简式为（）

    • A、Y=C
    • B、Y=BC+AB+BC
    • C、Y=ABC+AC+BC
    • D、Y=1

    正确答案:A

  • 第9题：

    逻辑函数式P=A+AB+ABC可化简为（）。

    • A、A
    • B、B
    • C、C
    • D、A+AB

    正确答案:A

  • 第10题：

    用3线-8译码器74LS138和辅助门电路实现逻辑函数F=A2+A2’A1’，应（）。

    • A、用与非门，F=（Y0’Y1’Y4’Y5’Y6’Y7’）’
    • B、用与门，F=Y2’Y3’
    • C、用或门，F=Y2’+Y3’
    • D、用或门，F=Y0’+Y1’+Y4’+Y5’+Y6’+Y7’

    正确答案:A,B

  • 第11题：

    用卡诺图化简逻辑函数的步骤除了将函数化简为最小项之和的形式外还有（）。

    • A、画出表示该逻辑函数的卡诺图
    • B、找出可以合并的最小项
    • C、写出最简“与或”逻辑函数表达式
    • D、写出最简“与或非”逻辑函数表达式

    正确答案:A,B,C

  • 第12题：

    单选题
    设y1＝e2x/2，y2＝exshx，y3＝exchx，则（　　）。
    A

    y1，y2，y3都没有相同的原函数

    B

    y2与y3有相同的原函数，但与y1的原函数不相同

    C

    y1，y2，y3有相同的原函数ex/（chx＋shx）

    D

    y1，y2，y3有相同的原函数ex/（chx－shx）


    正确答案： B
    解析：
    由于y1＝e2x/2，y2＝（e2x/2）－1/2，y3＝（e2x/2）＋1/2，故三个函数的原函数都不相同。

  • 第13题：

    试用代数法将如下逻辑函数式化简成最简与或式。(1) Y1=A－B＋A－BC－＋A－BCD＋A－BC－D－E(2) Y2=AB＋=AB——C＋A(3) Y3=AB＋(A－＋B－)C＋AB


    答案：(1) Y1=A-B+A-BC-+A-BCD+A-BC-D-E=A-B(2) Y2=AB+AB——C+A=A+C(3) Y3=AB+(A-+B-)C+AB=AB+C

  • 第14题：

    试用代数法化简如下逻辑函数式。(1) Y1=A(A＋B); (2) Y2=BC＋B－C; (3) Y3=A(A＋A－B)


    答案：(1) Y1=A(A+B)=A(2) Y2=BC+B-C=C (3) Y3=A(A+A-B)=A

  • 第15题：

    将如下逻辑函数式转换成最小项之和形式。(1) Y1=(A＋B－)(C＋B) (2) Y2=(A＋BC－)C(3) Y3=AB＋CD(AB－＋CD)(4) Y4=AB(B－C－＋BD)


    答案：(1) Y1=(A+B-)(C+B)=∑m(1,5,6,7)(2) Y2=(A+BC-)C=∑m(5,7)(3) Y3=AB+CD(AB-+CD)=∑m(3,7,1 1,1 2,1,3,1 4,1,5)(4) Y4=AB(B-C-+BD)∑m(1 3,1 5)

  • 第16题：

    使用与门、或]和非门,或者与门、或门和非门]的组合实现如下的逻辑函数式。(1) Y1=AB＋B—C (2) Y2= A(C—＋B) (3) Y3=ABC———＋B(EF＋G—)


    答案：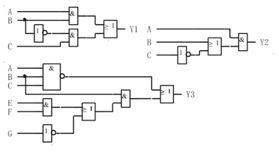

  • 第17题：

    逻辑函数的化简结果是:
    A. F=AB+BC
    C. F=A+B+C D. F=ABC


    答案：D
    解析：
    提示:由逻辑电路的基本关系变换可得结果，变换中用到了逻辑电路的摩根定理。

  • 第18题：

    下面的程序使用了函数指针，其运行结果是______。
    #include＜stdio.h＞#include＜math.h＞int f1（int a）{return a*a;}int f2（int a）{return a*a*a;}void main（ ）{int x=3,y1,y2,y3,y4;f=f1;y1=（*f）（x）;y2=f1（x）;f=f2;y3=f（x）;y4=f2（x）;printf（"y1=%d,y2=%d,y3=%d,y4=%d\n",y1,y2,y3,y4）;}

    A.y1=27,y2=9,y3=9,y4=27
    B.y1=9,y2=9,y3=27,y4=27
    C.y1=9,y2=27,y3=9,y4=27
    D.y1=27,y2=27,y3=9,y4=9

    答案：B
    解析：
    本题考查C语言函数指针的基础知识。仔细阅读程序，正确理解函数指针并将参数正确代入函数，可得到y1=9，y2=9，y3=27，y4=27的结果。

  • 第19题：

    逻辑函数式Y=A+A，化简后的结果是（）。

    A.2A
    B.A
    C.1
    D.A2

    答案：B
    解析：

  • 第20题：

    逻辑式A+AB的最简式为（）

    • A、A
    • B、AB
    • C、A+B
    • D、以上都不对

    正确答案:A

  • 第21题：

    用卡诺图化简逻辑函数，化简结果一般是最简或与式。


    正确答案:错误

  • 第22题：

    对于逻辑函数的化简，通常是指将逻辑函数化简成（）。

    • A、最简或与式
    • B、最简与或式
    • C、最简或非式
    • D、最简与非式

    正确答案:B

  • 第23题：

    单选题
    对于逻辑函数的化简，通常是指将逻辑函数化简成（）。
    A

    最简或与式

    B

    最简与或式

    C

    最简或非式

    D

    最简与非式


    正确答案： B
    解析： 暂无解析

相关内容