如下所示是一个带权连通无向图，其最小生成树各边权的总和为A． 24B．25C．26D．27

题目

如下所示是一个带权连通无向图，其最小生成树各边权的总和为

A． 24

B．25

C．26

D．27

相似考题

1.带权的连通无向图的最小(代价)生成树必是唯一的。()

2.图的生成树是不唯一的,一个连通图的生成树是一个最小连通子图,n个顶点的生成树有n－1条边,最小代价生成树是唯一的。( )此题为判断题(对，错)。

3.任何一个带权的无向连通图的最小生成树()。A.只有一棵B.有一棵或多棵C.一定有多棵D.n+2

4.连通图的各边权值均不相同，则该图的最小生成树是唯一的。()

更多“如下所示是一个带权连通无向图，其最小生成树各边权的总和为A． 24B．25C．26D．27”相关问题

  • 第1题：

    如图所示的带权无向图的最小生成树的权为 ( )

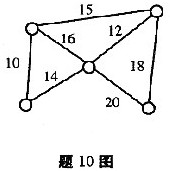
    A．51

    B．52

    C．54

    D．56


    正确答案：C
    解析：根据最小生成树的构造过程，可知在构造本题中无向图的最少生成树时，将选取权值分别为10、14、12、18的边，所以此最小生成树的权即各边权值之和即54。

  • 第2题：

    带权无向图的最小生成树是唯一的。

    此题为判断题(对，错)。


    正确答案：×

  • 第3题：

    任何一个带权的无向连通图的最小生成树( )

    A．只有一棵

    B．有一棵或多棵

    C．一定有多棵

    D．可能不存在


    正确答案：B

  • 第4题：

    已知某带权图G的邻接表如下所示，其中表结点的结构为：

    则图G是（ ）。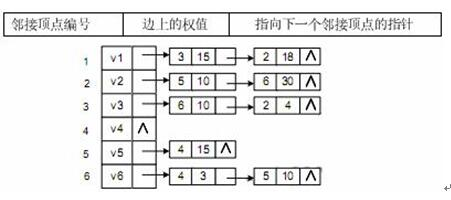

    A.无向图
    B.完全图
    C.有向图
    D.强连通图

    答案：C
    解析：
    本题考查数据结构基础知识。
    从题中的邻接表中可知，该图的边为、、、、、、、、，如下图所示，显然，这是个有向图。



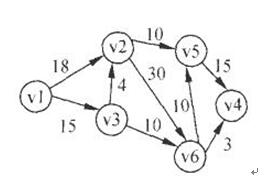
    在无向图中，若存在边（vi，vj），则它同时为vj和vi之间的边。在上面的邻接表中，存在边，而不存在，因此该图不是无向图。
    对于无向图，其边数e和顶点数n的关系为e=n×（n-1）/2。对于有向图，其边数e和顶点数n的关系为e = n×（n-1），因此该图不是完全图。
    若有向图为强连通图，则任意两个顶点间要存在路径。在该有向图中，由于顶点v4没有出边，因此，不存在v4到其他顶点的路径，因此该图不是强连通图。

  • 第5题：

    从赋权连通图中生成最小树，以下叙述（）不正确。

    • A、任一连通图生成的各个最小树，其总长度必相等
    • B、任一连通图生成的各个最小树，其边数必相等
    • C、任一连通图中具有最小权的边必包含在生成的最小树上
    • D、最小树中可能包括连通图中的最大权边

    正确答案:A,B,D

  • 第6题：

    带权连通图的最小生成树的权值之和一定小于它的其它生成树的权值之和。


    正确答案:正确

  • 第7题：

    一个带权无向图的最小生成树是否一定唯一？在什么情况下构造出的最小生成树可能不唯一？


    正确答案: 一个带权无向图的最小生成树不一定是唯一的。从Kruskal算法构造最小生成树的过程可以看出，当从图中选择当前权值最小的边时，如果存在多条这样的边，并且这些边与已经选取的边构成回路，此时这些边就不可能同时出现在一棵最小生成树中，对这些边的不同选择结果可能会产生不同的最小生成树。

  • 第8题：

    任何带权的无向图都存在最小（代价）生成树。


    正确答案:错误

  • 第9题：

    单选题
    最小生成树指的是（）。
    A

    由连通网所得到的边数最少的生成树

    B

    由连通网所得到的顶点数相对较少的生成树

    C

    连通网中所有生成树中权值之和为最小的生成树

    D

    连通网的极小连通子图


    正确答案： D
    解析： 暂无解析

  • 第10题：

    问答题
    一个带权无向图的最小生成树是否一定唯一？在什么情况下构造出的最小生成树可能不唯一？

    正确答案： 一个带权无向图的最小生成树不一定是唯一的。从Kruskal算法构造最小生成树的过程可以看出，当从图中选择当前权值最小的边时，如果存在多条这样的边，并且这些边与已经选取的边构成回路，此时这些边就不可能同时出现在一棵最小生成树中，对这些边的不同选择结果可能会产生不同的最小生成树。
    解析： 暂无解析

  • 第11题：

    判断题
    任何带权的无向图都存在最小（代价）生成树。
    A

    对

    B

    错


    正确答案： 错
    解析： 暂无解析

  • 第12题：

    单选题
    n个顶点的带权无向连通图的最小生成树包含（）个顶点。
    A

    n-1

    B

    n

    C

    n/2

    D

    n+1


    正确答案： B
    解析： 暂无解析

  • 第13题：

    己知某带权图G的邻接表如下所示，其中表结点的结构为：

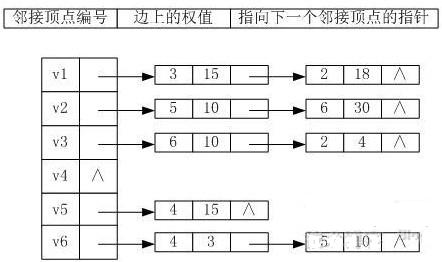
    则图G是______。

    A．无向图

    B．完全图

    C．有向图

    D．强连通图


    正确答案：C
    解析：本题考查数据结构基础知识。
    完全图是每对顶点之间都恰连有一条边的简单图。n个端点的完全图有n个端点及n(n ? 1) / 2条边。
    　　强连通图（Strongly Connected Graph）是指一个有向图（Directed Graph）中任意两点v1、v2间存在v1到v2的路径（path）及v2到v1的路径的图。
    　　从上面的表结构可以看出，有v1→v3的边，但没有v3→v1的边，显然这不是无向图，也不是完全图和强连通图，只能是有向图。

  • 第14题：

    如下所示是一个带权连通无向图，其最小生成树各边权的总和为

    A．24

    B．25

    C．26

    D．27


    正确答案：C

  • 第15题：

    对于含有n个顶点的带权连通图，它的最小生成树是指()。

    A.图中任意一个由n-l条权值最小的边构成的子图
    B.图中任意一个由n-1条权值之和最小的边构成的子图
    C.图中任意一个由n-1条权值之和最小的边构成的连通子图
    D.图中任意一个由n个顶点构成的边的权值之和最小的连通子图

    答案：D
    解析：
    一个连通图的生成树(连通无回路图)是一个极小连通子图。它含有图中全部n个项点，但只有构成一棵树的(n-1)条边。如果小于(n-1)条边，则是非连通图；如果多于(n-1)条边，则一定有回路，因为这条边使得它依附的那两个顶点之间有了第二条路径。但是，有(n-1)条边的图不一定都是生成树。带权连通无向图的所有生成树中具有边上的权值之和最小的树称为图的最小生成树。总之，含有n个顶点的带权连通图，它的最小生成树是指图中任意一个由n个顶点构成的边的权值之和最小的连通子图。

  • 第16题：

    对于一个带权连通图，在什么情况下，利用普里姆（Prim）算法与利用克鲁斯卡尔（Kruskal）算法可能生成不同的最小生成树？


    正确答案:当图中出现权值相同的边时，利用普里姆(Prim)算法与利用克鲁斯卡尔(Kruskal)算法可能生成不同的最小生成树。

  • 第17题：

    n个顶点的带权无向连通图的最小生成树包含（）个顶点。

    • A、n-1
    • B、n
    • C、n/2
    • D、n+1

    正确答案:B

  • 第18题：

    最小生成树指的是（）。

    • A、由连通网所得到的边数最少的生成树
    • B、由连通网所得到的顶点数相对较少的生成树
    • C、连通网中所有生成树中权值之和为最小的生成树
    • D、连通网的极小连通子图

    正确答案:C

  • 第19题：

    对于含有N个顶点E条边的无向连通图，利用Kruskal算法生成最小代价生成树的时间复杂度为（）。


    正确答案:o（elg0）

  • 第20题：

    若连通网络上各边的权值均不相同，则该图的最小生成树有（）棵。


    正确答案:1

  • 第21题：

    填空题
    对于含有N个顶点E条边的无向连通图，利用Kruskal算法生成最小代价生成树的时间复杂度为（）。

    正确答案： o（elg0）
    解析： 暂无解析

  • 第22题：

    填空题
    若连通网络上各边的权值均不相同，则该图的最小生成树有（）棵。

    正确答案： 1
    解析： 暂无解析

  • 第23题：

    判断题
    带权连通图的最小生成树的权值之和一定小于它的其它生成树的权值之和。
    A

    对

    B

    错


    正确答案： 对
    解析： 暂无解析

相关内容