下列关于函数依赖和多值依赖的叙述中，哪些是不正确的?I．若x→Y，则x→YⅡ．若X→Y，则x→YⅢ．若Y∈x，则x→YIV．若Y∈x，则x→→YV．若x→Y，Y’<Y，则x→Y’VI．若X→→Y，Y’cY则x→→Y’A．仅II、Ⅳ和VB．仅I、III和ⅣC．仅II和VID．仅Ⅳ和VI

题目

下列关于函数依赖和多值依赖的叙述中，哪些是不正确的?

I．若x→Y，则x→Y

Ⅱ．若X→Y，则x→Y

Ⅲ．若Y∈x，则x→Y

IV．若Y∈x，则x→→Y

V．若x→Y，Y’<Y，则x→Y’

VI．若X→→Y，Y’cY则x→→Y’

A．仅II、Ⅳ和V

B．仅I、III和Ⅳ

C．仅II和VI

D．仅Ⅳ和VI

相似考题

1.（ 52 ）下列关于函数依赖和多值依赖的叙述中，哪些是不正确的？I ． 若 X → Y, 则 X →→ Y Ⅱ ．若 X →→ Y, 则 X → YⅢ ．若 Y ? X, 则 X → Y Ⅳ ．若 Y ? X, 则 X →→ YⅤ ．若 X → Y, Y ’ ? X, 则 X → Y ’ Ⅵ ．若 X →→ Y, Y ’ ? Y, 则 X →→ Y ’A ） Ⅱ 和 ⅣB ） Ⅰ 、 Ⅲ 和 ⅣC ） Ⅱ 和 ⅥD ） Ⅳ 和 Ⅵ

2.（ 52 ）下列关于函数依赖和多值依赖的叙述中，哪些是不正确的？I. 若 X → Y ，则 X →→ Y II. 若 X →→ Y ，则 X → YIII. 若 YcX ，则 X → Y IV. 若 YcX ，则 X →→ YV. 若 X → Y, Y' c Y ，则 X → Y' VI. 若 X →→ Y ， Y' a Y ，则 X →→ Y'A ）仅 II 、 IV 和 VB ）仅 I 、 III 和 IVC ）仅 II 和 VID ）仅 IV 和 VI

3.下列关于多值依赖的叙述中，不正确的是A．若X→→Y，则X→→Z，其中Z＝U-X-YB．若X→→Y，而Z=，则称X→→Y为平凡的多值依赖C．若X→Y，则X→→YD．若X→→Y，则X→Y

4.（53）下列关于函数依赖和多值依赖的叙述中，（ ）是不正确的。Ⅰ、若X→Y，则X→→Y Ⅱ、若X→→Y，则X→YⅢ、若Y í X，则X→Y Ⅳ、若Y í X，则X→→YⅤ、若X→Y，Y* ì Y，则X→Y* Ⅵ、若X→→Y，Y*ìY，则X→→Y*A）仅Ⅱ和ⅣB）仅Ⅰ、Ⅱ和ⅣC）仅Ⅱ和ⅥD）仅Ⅳ、Ⅴ和Ⅵ

更多“下列关于函数依赖和多值依赖的叙述中,哪些是不正确的?I.若x→Y,则x→YⅡ.若X→Y,则x→YⅢ.若Y∈x,则x→YI ”相关问题

  • 第1题：

    下列关于多值依赖的叙述中，不正确的是

    A．若X→→Y，则X→→Z，其中Z=U-X-Y

    B．若X→→Y，而，则称X→→Y为平凡的多值依赖

    C．若X→Y，则X→→Y

    D．若X→→Y，则X→Y


    正确答案：D

  • 第2题：

    下列关于多值依赖的叙述中，不正确的是

    A．若X→→Y，则X→→Z，其中Z=U-X-Y

    B．若X→→Y，而Z=?，则称X→→Y为平凡的多值依赖

    C．若X→Y，则X→→Y

    D．若X→→Y，则X→Y


    正确答案：D
    解析：若X→→Y，则X→→Z，其中Z=U-X-Y，即多值依赖具有对称性；若 X→→Y，而Z=?，则称X→→Y为平凡的多值依赖；若X→Y，则X→→Y，即函数依赖可以看做多值依赖的特殊情况。注意：若X→→,Y，则X→Y和多值依赖的特殊情况正好相反。

  • 第3题：

    下列关于函数依赖和多值依赖的叙述中，不正确的是( )。

    Ⅰ、若X→Y， 则X→→Y

    Ⅱ、若X→→Y， 则X→Y

    Ⅲ、若YX，则X→Y

    Ⅳ、若Y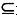X，则X→→Y

    Ⅴ、若X→Y，Y*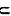Y， 则X→Y*

    Ⅵ、若X→→Y，Y*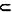Y， 则X→→Y*

    A．仅Ⅱ和Ⅳ

    B．仅Ⅰ、 Ⅱ和Ⅳ

    C．仅Ⅱ和Ⅵ

    D．仅Ⅳ、Ⅴ和Ⅵ


    正确答案：B
    解析：Armstrong公理系统包括以下3条推理规则。设F是属性组U上的一组函数依赖，于是有以下推理规则：①自反律。若Y∈X∈U，则X→Y为F所逻辑蕴含。②增广律．若X→Y为P所逻辑蕴含，且Z∈U，则XZ→YZ为F所逻辑蕴含。③传递律。若X→Y即Y→Z为F所逻辑蕴含，则X→Z为F所逻辑蕴含。若X→→Y，而Z=Φ，则称X→→Y为平凡的多值依赖。若X→→Y在R(U)上成立，用Y'∈Y，我们不可以断言X→→y'成立。设R是属性集U上的一个关系模式，X、Y是U的子集，Z=U-X-Y，多值依赖的性质如下：①若X→→Y，则X→→Z，其中Z=U-X-Y，即多值依赖具有对称性。②若X→Y，则X→→Y，即函数依赖可以看作多值依赖的特殊情况。③设属性集之间的关系是XY∈W∈U，那么当X→→Y在R(U)上成立的时候，X→→Y在R(W)上也成立；反过来当X→→Y在R(W)上成立时，X→→Y在R(U)上不一定成立。④若X→→Y，且Y'∈Y，但不能断言X→→Y'也成立。因为多值依赖的定义中涉及了U中除X、Y之外的其余属性Z，考虑X→→Y'是否成立时涉及的其余的属性Z'=U-X-Y'比确定X→→Y成立时的其余属性Z=U-X-Y包含的属性列多，因此X→→Y'不一定成立。

  • 第4题：

    设U为所有属性，X, Y, Z为属性集，Z=U一X一Y。下列关于函数依赖和多值依赖的叙述中，哪些是正确的？

    I．若X→Y,则X→→＊Y

    II．若X→→Y,则X→Y

    III．若X→Y,则X→Z

    IV．若X→→Y，则X→→Z

    V．若X→→Y, Y'Y,则X→→Y'

    A．仅I、II和III

    B．仅II、III和V

    C．仅I和IV

    D．仅IV和V


    正确答案：C

  • 第5题：

    下列关于函数依赖和多值依赖的叙述中，不正确的是( )。

    Ⅰ．若X→Y， 则X→→Y

    Ⅱ．若X→Y， 则X→Y

    Ⅲ． 若YX，则X→Y

    Ⅳ、若YX，则X→→Y

    Ⅴ． 若X→Y，Y*Y， 则X→Y*

    Ⅵ．若X→→Y，Y*y， 则X→→Y，

    A．Ⅱ和Ⅳ

    B．Ⅰ、Ⅲ和Ⅳ

    C．Ⅱ和Ⅵ

    D．Ⅳ和Ⅵ


    正确答案：C
    解析：若X→→Y，且Y'∈Y，但不能断言X→→Y'也成立。因为多值依赖的定义中涉及了U中除X、Y之外的其余属性Z，考虑X→→Y'是否成立时涉及的其余的属性Z'=U-X-Y确定X→→Y成立时的其余属性Z=U-X-Y包含的属性列多，因此X→→Y'不一定成立。若X→Y，则X→→Y，即函数依赖可以看作多值依赖的特殊情况，但反之则不成立。

相关内容