用补码表示的一个n位带符号的整数,其有效数值范围是A.-2n~2nB.-2n~2n-1C.-2n-1~2n-1D.-2n-1~2n-1-1
题目
用补码表示的一个n位带符号的整数,其有效数值范围是
A.-2n~2n
B.-2n~2n-1
C.-2n-1~2n-1
D.-2n-1~2n-1-1
相似考题
参考答案和解析
正确答案:D
解析:带符号的整数必须使用一个二进位作为其符号位,一般总是最高位(最左面的一位),“0”标识“+”(正数),“1”标识“-”(负数),其余各位则用来表示数值的大小。数据的补码表示仅当负数时才与原码有所不同。无符号二进制整数的原码,其编码与数值之间的关系如下。
设KnKn-1...K1K0用来表示带符号整数时,Kn是符号位,Kn-1...K1K0则为数值位。若KnKn-1...K1K0表示的是原码编码的整数,则十进制数值S与编码的关系是:
S=Kn-1×2n-1+...+K1×21+K0×20(当Kn=0)
S=-(Kn-1×2n-1+...+K1×21+K0×20)(当Kn=1)
但是,如果KnKn-1...K1K0表示的是补码编码的整数时,不论符号位Kn如何,十进制数值S与编码的关系可以统一地表示为:
S=Kn×(-2n)+Kn-1×2n-1...+K1×21+K0×20
由此可见,采用补码表示的n位二进制带符号整数的有效范围是:
-2n-1
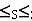
n-1-1,选项D正确。
解析:带符号的整数必须使用一个二进位作为其符号位,一般总是最高位(最左面的一位),“0”标识“+”(正数),“1”标识“-”(负数),其余各位则用来表示数值的大小。数据的补码表示仅当负数时才与原码有所不同。无符号二进制整数的原码,其编码与数值之间的关系如下。
设KnKn-1...K1K0用来表示带符号整数时,Kn是符号位,Kn-1...K1K0则为数值位。若KnKn-1...K1K0表示的是原码编码的整数,则十进制数值S与编码的关系是:
S=Kn-1×2n-1+...+K1×21+K0×20(当Kn=0)
S=-(Kn-1×2n-1+...+K1×21+K0×20)(当Kn=1)
但是,如果KnKn-1...K1K0表示的是补码编码的整数时,不论符号位Kn如何,十进制数值S与编码的关系可以统一地表示为:
S=Kn×(-2n)+Kn-1×2n-1...+K1×21+K0×20
由此可见,采用补码表示的n位二进制带符号整数的有效范围是:
-2n-1
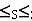
n-1-1,选项D正确。
更多“用补码表示的一个n位带符号的整数,其有效数值范围是A.-2n~2nB.-2n~2n-1C.-2n-1~2n-1D.-2n-1~2n-1 ”相关问题
-
第1题:
等式[x]补+[Y]补=[x+Y]补在满足条件(92)时成立,其中X、Y是用n个二进制位表示的带符号纯整数。
A.-2n≤(X+Y)≤2n-1
B.-2n-1≤(X+Y)<2n-1
C.-2n-1-1≤(X+Y)≤2n-1
D.-2n-1≤(X+Y)<2n
正确答案:B
解析:补码运算对于表示范围内的加法是成立的,范围外的不成立。n位补码表示的范围是[-2n-1,2n-1-1],所以X+Y的表示范围是[-2n,2n-2],但是当X+Y=2n-1时,得到的补码表示-2n-1,此时补码加法得到的结果是错误的,所以对于超出表示范围的运算,补码加法是不成立的。 -
第2题:
用8位二进制数的补码形式表示一个带符号数,它能表示的整数范围是()。
A -127-+127
B -128-+128
C -127-+128
D -128-+127
D
略 -
第3题:
对于一个带符号的二进制数,其最高位表示符号位,其余部分表示数值位,所以一个用补码表示的4位带符号二进制数 1001表示的是十进制数 –1。
正确 -
第4题:
用n个二进制位表示带符号纯整数时,已知[X]补、[Y]补,则当 (1) 时,等式[X]补+[X]补=[X+Y]补成立。
A.-2n≤(X+Y)≤2n-1
B.-2n-1≤(X+Y)<2n-1
C.-2n-1-1≤(X+Y)≤2n-1
D.-2n-1≤(X+Y)<2n
正确答案:B
解析:这个问题实际上考查补码能够表示的范围,由于补码中的0有唯一的表示,因此当编码总位数为n时,补码能表示2n个数。 -
第5题:
对于一个带符号的二进制数,其最高位表示符号位,其余部分表示数值位,所以一个用补码表示的4位带符号二进制数 1001表示的是十进制数 –1。对吗?
-5
