计算不定积分∫(x)√(2＋x^2)dx.

题目
计算不定积分∫(x)√(2＋x^2)dx.

相似考题

1.曲线y=x/(2+x)的铅直渐近线为______

2.求解一道公务员数量关系题已知F(x）=x^2+ax+3 F(2+x）=F(2-x）则F（2）是多少 给出的答案是-1 并且是说 因为F(2+x）=F(2-x）所以说对称抽为x=2 那么-a/2=2 为什么对称轴是X=2 为什么-a/2=2 哪位能解释的详细一些啊 高中的东西4年没看了 大学也不接触 实在忘了 希望能有好心人 帮忙详细解答一下 谢谢问题补充：怎么利用等式f(2+x)=f(2-x),求a值 根据什么公式或者定理

3.根据下列条件求正整数x：（1）x+2＜6 ；（2）2x+5＜10；（3）x-3/2≥2x-5/3；（4）2+x/2≥2x-1/3-2.

4.d(sin2x+cosx)=_________dx.

更多“计算不定积分∫(x)√(2＋x^2)dx. ”相关问题

  • 第1题：

    已知f(x)=x2+ax+3，若f(2+x)=f(2-x)，则f(2)=（）。

    A.0

    B.-1

    C.-2

    D.-3


    正确答案：B
    32.B【解析】由f(2+x)=f(2-x)可知该函数对称轴为x=2，而根据f(x)=x2+ax+3，可知该函数为二次函数。那么根据二次函数的性质，可知a=(-2)×1×2=-4，则f(2)=22+(-4)×2+3=-1，所以答案为B项。

  • 第2题：

    不定积分=( )。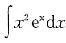

    A ex(x2+2x-2)+C
    B ex(x2+2x+2)+C
    C ex(x2-2x+2)+C
    D ex(x2-2x-2)+C

    答案：C
    解析：
    由分部积分法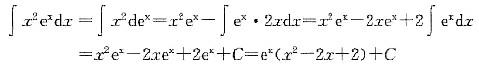

  • 第3题：

    [（2+x)（2+x)（x)]/[（3-x)（3-x)（3-x)]=0.00001，则x的取值范围是

    A．-∞~ -0.00001

    B．-0.00001~0

    C．0~0.00001

    D．0.00001~ +∞


    0,1,3,6

  • 第4题：

    数学运算

    已知f(x)＝x2+ax+3，若f(2+x)＝f(2-x)，则f(2)＝( )。

    A．0

    B．-1

    C．-2

    D．3


    正确答案：B
    [解析]本题答案为B。本题属于函数问题。由f(2+x)＝f(2-x)知道函数f(x)的对称轴为x＝ 2，因此-(a/2)＝2，a＝-4。所以f(2)＝22-2×4+3＝-1。

  • 第5题：

    设函数y=f(x)由方程y^3+xy^2+x^2y+6=0确定，求f(x)的极值.


    答案：
    解析：

相关内容