教师教学数学思想方法的主要阶段有()。A.多次孕育B.深化应用C.初步理解D.简单应用

题目
教师教学数学思想方法的主要阶段有()。

A.多次孕育

B.深化应用

C.初步理解

D.简单应用

相似考题

1.数学基础知识和数学思想方法是数学教学的两条主线。()此题为判断题(对，错)。

2.简述数学教学原则中的“渗透数学思想方法原则”

3.数学思想方法教学为什么要遵循循序渐进原则?试举例说明。

4.鉴于数学思想方法有浅显与深奥之分、具体与抽象之别,因而数学思想方法各个教学阶段的划分也是()的。A.确定B.相对C.绝对D.固定

更多“教师教学数学思想方法的主要阶段有()。 ”相关问题

  • 第1题：

    简述中学数学思想方法的教学原则中的系统性原则。


    答案：
    解析：
    数学思想方法的教学与具体数学知识教学一样，只有形成具有一定结构的系统，才能更好地发挥其整体功能。所谓系统性原则是指为了使学生更好地理解和掌握数学思想方法，教师应把握好每一种数学思想与它所概括的一类数学方法、所串联的具体数学知识形成的体系，并有计划、有目的、有层次地在教学中予以落实。

  • 第2题：

    小学数学思想方法教学的主要阶段是形象（），即由具体形象思维向（）思维的过渡阶段。
    抽象思维；抽象逻辑
    略

  • 第3题：

    设计一个教学实例，说明其中蕴含的数学思想方法。


    √

  • 第4题：

    请认真阅读下列材料，并按要求作答。


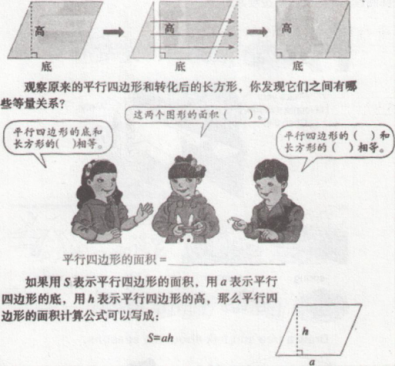
    请根据上述材料完成下列任务：
    (1)什么是数学思想方法指出本节课所用到的数学思想方法。
    (2)若指导中年段小学生学习，试拟定教学目标。
    (3)依据拟定的教学目标，设计课堂教学的主要环节，并简要说明理由。


    答案：
    解析：
    (1)数学思想方法是数学思想与数学方法的合称。数学思想是指从具体的数学内容中提炼出来的对数学知识的本质认识，它在数学认识活动中被普遍使用，是建立数学理论和解决数学问题的指导思想。数学方法是指在研究数学问题的过程中所采用的各种方式、手段、途径、步骤、程序等，它通过一些可操作的规则或模式达到某种预期的目的。 本节课用到了转化、符号化的数学思想方法。转化思想方法是由一种形式变换成另一种形式的思想方法，而其本身的大小是不变的。如几何的等积变换、解方程的同解变换、公式的变形等。符号化思想方法是用符号化的语言(包括字母、数字、图形和各种特定的符号)来描述数学内容。如数学中各种数量关系，量的变化及量与量之间进行推导和演算，都是用小小的字母表示数，以符号的浓缩形式表达大量的信息，如定律、公式等。
    (2)教学目标
    知识与技能目标：理解利用数方格、割补和拼摆等方法求平行四边形面积的方法，能够运用平行四边形面积的计算公式计算平行四边形的面积。
    过程与方法目标：通过观察、操作、比较等活动，渗透“转化”的思想，发展观察、分析、概括、推导的能力。
    情感态度与价值观目标：感受数学与生活的联系，提高数学应用意识，体验数学的价值。
    (3)教学环节
    (一)直接导入，激发兴趣
    创设动画人物情境：兔妈妈在山上开垦了两块地，决定把地交给两只兔宝宝来种。(课件出示两块地)老大说：“我是哥哥。我来种大的。可这两块地到底哪块大呢”你能帮它解决这个问题吗
    提问：长方形的面积大家会求，那平行四边形的面积呢揭示课题并板书“平行四边形的面积”。
    【设计意图】
    通过创设问题情境使学生感受到数学无处不在，感受数学的魅力。通过质疑“这两块地到底哪块大呢”使学生产生求知的欲望，激发学生积极探索的兴趣。
    (二)合作交流，探索新知
    1．用数方格(即数面积单位)的方法来计算平行四边形的面积。
    提问：我们怎样才能知道平行四边形的面积呢
    学生可讨论说出亲自量量、摆摆、数数等方法，教师顺势引出数方格的方法。
    ①课件出示方格图和表格并说明要求(一个方格代表1平方米，不满一个按半格计算)，学生独立完成数方格和填表的任务。
    ②认真观察，探索发现。为了让学生认真观察表格，提出问题：“你觉得平行四边形的面积可能会怎样求”
    引出猜测：平行四边形的面积=底X高。
    【设计意图】
    通过让学生用数一数、填一填、说一说建立平行四边形与长方形的联系，同时培养学生敢于联想、大胆猜测的能力，也为下一步探索平行四边形面积的计算方法提供思路。
    2．渗透“转化”思想引入割补法。
    ①引导学生独立思考，寻求验证方法。
    提问：通过刚才的方法我们猜测平行四边形的面积=底×高，那么是否成立呢接下来我们验证一下：不数方格，能不能计算平行四边形的面积呢能不能把它转化成学过的图形呢
    ②动手操作。(先让学生自己动手剪一剪、拼一拼，再四人小组交流剪、拼的过程，并求出平行四边形的面积)
    ③学生演示剪、拼的过程。(课件展示两种剪法)
    展示之后问：“为什么要沿着高剪开呢”使学生明白只有沿着高剪，才能拼成长方形。
    3．建立联系，推导公式。
    提问：现在会求平行四边形的面积吗怎样求为什么
    学生异口同声回答：将平行四边形转化成长方形来求平行四边形的面积即平行四边形的面积=长×宽。
    追问：今后所有的平行四边形都需要割补成长方形吗如一块草坪不能割补怎么办根据刚才转化的过程你能发现点什么学生思考．四人小组讨论。
    【设计意图】
    通过一系列的追问迫使学生独立思考，发现平行四边形与转化后的长方形的关系．学生的叙述也能帮助学生深化理解知识的形成过程。
    4．公式强化，字母表示
    学生自学平行四边形面积的字母形式，根据学生的汇报板书：S=ah。
    (三)运用新知
    1．已知平行四边形的面积。求这个平行四边形的高是多少
    2．可以再画一个与已知平行四边形面积相等的平行四边形吗能画几个
    设计意图：使学生认识到等底等高的平行四边形面积相等。因此可以画出无数个平行四边形。
    (四)小结作业
    1．全课小结：通过这节课的学习。谁愿意和大家一起来分享你的收获
    【设计意图】
    通过让学生谈收获以此来培养学生对知识的归纳、整理、概括的能力，同时也培养了学生的语言表达能力：
    还包括对“转化”这一思想方法的运用理解，这是数学由“双基”转化“四基”的具体体现。
    2．拓展运用：我准备了一个可活动的长方形框架，如果把它拉成一个平行四边形，周长和面积有变化吗怎样变化如果任意拉这个平行四边形，你会发现什么什么情况下它的面积最大
    【设计意图】
    通过这个拓展题目使学生体会平行四边形面积的变化，从而理解得更透彻，运用得更灵活。使学生在练习中思维得到发展，培养学生分析问题和解决问题的能力。

  • 第5题：

    试述数形结合的思想方法及其在中学数学教学中的作用。


    全体同学参与的“动手操作”让人较深刻的认识了定义的本质属性;把数形结合思想运用到课后的作业中;初步形成一种思考问题的方式

相关内容