下面的函数模板定义中错误的是A．templateB．template Q F(Q x){retum Q+x;) Q F(Q x){return x+x;}C．template＜classT＞D．template＜class T＞ TF(T x){return x*x;) Bool F(tx){return x＞1;)

题目

下面的函数模板定义中错误的是

A．template

B．template Q F(Q x){retum Q+x;) Q F(Q x){return x+x;}

C．template＜classT＞

D．template＜class T＞ TF(T x){return x*x;) Bool F(tx){return x＞1;)

相似考题

1.（ 13 ）在有理数类 Rational 中重载插入运算符 << ，以便按 a/q 形式输出。请将 << 运算符函数的定义补充完整。class Rational{public:Rational(int aa, int qq):a(aa),q(qq){ }friend 【 14 】 operator<<(ostream &out, Rational &x){return (out<<x.a<< ' / ' <<x.q);}private:int a,q;};

2.以下程序的输出结果是include "stdio.h"int *f(int *x,int *y){ if(*x<*y) return x; else return y;}main(){ int a=7,b=8, *p,*q,*r ; p=&a; q=&b; r= f(p,q); printf("%d,%d,%d\n",*p,*q,*r);}

3.对序列(Q，D，F，X，A，P，N，D，Y，M，C，W)按照字典顺序采用二路归并方法进行排序，下面的4个序列中(54)是第三趟的结果。A．A，B，D，F，N，P，Q，X，C，W，M，YB．A，B，P，D，N，P，Q，X，C，M，W，YC．A，B，D，F，P，Q，X，N，C，M，W，YD．A，B，D，P，N，P，Q，X，C，M，W，Y

4.阅读下列函数说明和C函数，将应填入(n)处的字句写在对应栏内。[说明]循环队列的类型定义如下(其中队列元素的数据类型为datatype)：typedef struct{datatype data[MAXSIZE]; /*数据的存储区*/int front,rear; /*队首、队尾指针*/int num; /*队列中元素的个数*/}c _ SeQueue; /*循环队*/下面函数及其功能说明如下：(1) c_SeQueue* Init_SeQueue()：新建队列；(2) int ln_SeQueue( c_SeQueue *q, datatype x)：将元素x插入队列q，若成功返回1否则返回0；(3) int Out_SeQueue (c_SeQueue *q, datatype *x)：取出队列q队首位置的元素，若成功返回1否则返回0。[函数]c_SeQueue* Init_SeQueue(){ q=malloc(sizeof(c_SeQueue));q-＞front=q-＞rear=MAXSIZE-1;(1);return q;}int In_SeQueue( c_SeQueue *q, datatype x){ if(q-＞num= =MAXSIZE) return 0; /*队满不能入队*/else {q-＞rear=(2);q-＞data[q-＞rear]=x;(3);return 1; /*入队完成*/}}int Out_SeQueue( c_SeQueue *q, datatype *x){ if (q-＞num= =0) return 0; /*队空不能出队*/else{*x=(4); /*读出队首元素*/q-＞front=(5);q-＞num- -;return 1; /*出队完成*/}}

参考答案和解析
正确答案：A
更多“下面的函数模板定义中错误的是A.templateB.template Q F(Q x){retum Q＋x;) Q F(Q x){return ”相关问题

  • 第1题：

    如果希望循环队列中的向量单元都能得到利用，则可设置一个标志域tag，每当尾指针和头指针值相同时，以tag的值为O或1来区分队列状态是“空”还是“满”．请对下列函数填空，使其分别实现与此结构相应的入队列和出队列的算法．

    intEnQueue(CirQueue*Q,DataType x)

    {

    if Q->tag==1 return 0；

    Q->data[Q->rear]=x；

    Q->rear=(Q->rear+1)%MAXQSIZE

    if(Q->rear==Q->front)Q->tag=1

    return1：

    }

    intDeQueue(CirQueue*Q,DataType*x)

    {

    if(（1）)return0；

    *x=Q->data[Q->front];

    Q->front= (2) ；

    (3) ；

    return1；

    }

    (1)

    (2)

    (3)


    正确答案：

    (1)Q->tag= =0(或者！Q->tag)／／如果标志域tag为0，则队空，无法出队，算法结束；
    (2)(Q->front+l)% MAXQSIZE／／出队，头指针循环加1；
    (3)if(Q->rear= =Q->front)Q->tag=0;／／出队后，则检查尾指针是否等于头指针，若相等，则队空，置标志域tag为0．

  • 第2题：

    （)不是有效的推理。

    A．前提：("x)(~P(x)ÞQ(x)), ("x)~Q(x) 结论：P(a)

    B．前提：("x)(P(x)ÞQ) 结论：("x)P(x)ÞQ

    C．前提：("x)(P(x)∨Q(x)), ("x)(Q(x)Þ~R(x)) 结论：($x)(R(x)ÞP(x))

    D．前提：("x)(P(x)Þ(Q(x)∧R(x))), ($x)(P(x)∧S(x)) 结论：("x)(R(x)∧S(x))

    E．前提：("x)($y)P(x, y) 结论：("x)($y)($z)(P(x, y)∧P(y, z))

    F．前提：("x)P(x)∨("x)Q(x) 结论：("x)(P(x)∨Q(x))

    G．前提：("x)(G(x)ÞH(x))，~($x)(F(x)∧H(x)) 结论：($x)F(x)Þ($x)G(x)

    H．前提：("x)(H(x)ÞM(x)) 结论：("x)("y)(H(y)∧N(x, y


    等值关系;蕴涵关系

  • 第3题：

    Q=f（L，K），或Q=f（K，L）,表示短期生产函数，Q=f（L，K）表示长期生产函数。


    K

  • 第4题：

    如果函数f(x)=在x=0处连续，则p、q的值为:
    A.p=0,q=0 B.p=0,q=1 C.p=1,q=0 D.p=1,q=1


    答案：D
    解析：
    提示：利用函数在x=0点连续的定义f(x+0)=f(x-0)=f(0)，求p、q值。


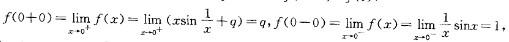
    f(0)=p，求出 p=q=1。

  • 第5题：

    【单选题】若f（x)的常数项a0=±1,令g（x)=f（x+b),b=1或-1，如果g（x)在Q上不可约那么（）。

    A．f(x）在Q不可约

    B．f(g(x+b)）在Q不可约

    C．f(g(x)）在Q不可约

    D．g(f(x）)在Q不可约


    f（x）在Q不可约

  • 第6题：

    函数f（x)=2（1+x2)， -1 ＜ x ＜ 1，为了保持最大精度，试确定定点运算时自变量x和函数f（x)的Q值。


    R Y (t 1 ,t 2 )=E[Y(t 1 )Y(t 2 )]=E[X(t 1 )(t 1 +1)X(t 2 )(t 2 +1)]=(t 1 +1)(t 2 +1)E[X(t 1 )X(t 2 )]=(t 1 +1)(t 2 +1)R X (t 1 ,t 2 )$R Z (t 1 , t 2 )=E[Z(t 1 )Z(t2)]=E[cX(t 1 )cX(t 2 )]=c 2 E[X(t 1 )X(t 2 )]=c 2 R X (t 1 ,t 2 )

相关内容