已知a所指的数组中有N个元素。。函数fun的功能是,将下标k(k>0)开始的后续元素全部向前移动一个位置填空。void fun(int a[N],int k){int i:for(i=k;i ]=—a[i];}
题目
已知a所指的数组中有N个元素。。函数fun的功能是,将下标k(k>0)开始的后续
元素全部向前移动一个位置填空。
void fun(int a[N],int k)
{int i:
for(i=k;i ]=—a[i];
}
相似考题
参考答案和解析
i--1
更多“已知a所指的数组中有N个元素。。函数fun的功能是,将下标k(k>0)开始的后续元素全部向前移动一个 ”相关问题
-
第1题:
已知有一维数组T[0..m*n-1],其中m>n。从数组T的第一个元素(T[0])开始,每隔n个元素取出一个元素依次存入数组B[1..m]中,即B[1]=T[0],D[2]=T[n],依此类推,那么放入B[k](1≤k≤n)的元素是______。
A.T[(k-1)*n]
B.T(k*n)
C.T[(k-1)*m]
D.T[k*m]
正确答案:A
解析:根据题意,每隔n个元素取出一个元素依次存入数组B(1..m]中。所以,不难推导出B[1]=T[0],B[2]=T[n],B[3]=T[2n],…,B[k]=T[(k-1)n]故本题应该选择A。 -
第2题:
阅读下列函数说明和C代码,将应填入(n)处的字句写在答题纸的对应栏内。
【说明】
函数void rcr(int a[],int n,int k)的功能是:将数组a中的元素a[0]~a[n-1]循环向右平移k个位置。
为了达到总移动次数不超过n的要求,每个元素都必须只经过一次移动到达目标位置。在函数rcr中用如下算法实现:首先备份a[0]的值,然后计算应移动到a[0]的元素的下标p,并将a[p]的值移至a[0];接着计算应移动到a[p]的元素的下标q,并将a[q]的值移至a[p];依次类推,直到将a[0]的备份值移到正确位置。
若此时移动到位的元素个数已经为n,则结束;否则,再备份a[1]的值,然后计算应移动到a[1]的元素的下标p,并将a[p]的值移至a[1];接着计算应移动到a[p]的元素的下标q,并将a[q]的值移至a[p];依次类推,直到将a[1]的备份值移到正确位置。
若此时移动到位的元素个数已经为n,则结束;否则,从a[2]开始,重复上述过程,直至将所有的元素都移动到目标位置时为止。
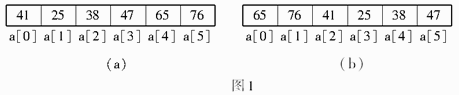
例如,数组a中的6个元素如图1(a)所示,循环向右平移两个位置后元素的排列情况如图1(b)所示。
【函数】
void rcr(int a[],int n,int k)
{int i,j,t,temp,count;
count=0;/*记录移动元素的次数*/
k=k%n;
if( (1) ){/*若k是n的倍数,则元素无须移动;否则,每个元素都要移动*/
i=0;
while(count<n){
j=i;t=i;
temp=a[i];/*备份a[i]的值*/
/*移动相关元素,直到计算出a[i]应移动到的目标位置*/
while((j= (2) )!=i){
a[t]=a[j];
t= (3) ;
count++;
}
(4) =temp;count++;
(5) ;
}
}
}
正确答案:
【答案】(1)k或k!=0(2)(j-k+n)%n或(t-k+n)%n(3)j(4)a[t]或等价表达式(5)i++或等价表达式【解析】(1)判断k执行k=k%n后是否为0,即是否是n的倍数,应填入k或k!=0。(2)j表示要移动到a[t]的元素的位置,于是j和t的关系为j=(t-k+n)%n;当执行完j=i,t=i后,j=t,于是此处可填入(j-k+n)%n或(t-k+n)%n。(3)将a[j]移动到a[t]后,需要将t指向j,即此处填入j。(4)将暂存在temp中的值移动到a[t]中。即此处填入a[t]或等价表达式。(5)此处while循环的递增条件,显然应该是i++或其他等价表达式。 -
第3题:
已知有一维数组T[0...m*n-1],其中m>n。从数组T的第一个元素(T[0])开始,每隔n个元素取出一个元素依次存入数组B[1...m]中,即B[1]=T[0],B[2)= T[n],依次类推,那么放入B[k](1≤k≤m)的元素是( )。A.T[(k-1)*n]
B.T[k*n]
C.T[(k-1)*m]
D.T[k*m]答案:A解析:由题可知,B[1]=T[(1-1)*n],B[2]=T[(2-1)*n],B[3]=T[(3-1)*n],...,根据归纳法可得B[k]=T[(k-1)*n)。 -
第4题:
已知有一维数组T[0...m*n-1],其中m>n。从数组T的第一个元素(T[0])开始,每隔n个元素取出一个元素依次存入数组B[1...m]中,即B[1]=T[0],B[2)= T[n],依次类推,那么放入B[k](1≤k≤m)的元素是______。
A.T[(k-1)*n]
B.T[k*n]
C.T[(k-1)*m]
D.T[k*m]
正确答案:A
解析:由题可知,B[1]=T[(1-1)*n],B[2]=T[(2-1)*n],B[3]=T[(3-1)*n],...,根据归纳法可得B[k]=T[(k-1)*n)。 -
第5题:
(11)己知a所指的数组中有N个元素。函数fun的功能是,将下标k(k>0)开始的后续元素全部向前移动一个位置。请填空。
void fun(int a[N],int k)
{ int i;
for(i=k;i<N;i++) a[ 【11】 ]=a[i];
}
正确答案:
(11)i-1
