已知一个图的顶点集V和边集E分别为: V={A,B,C,D,E,F,G}; E={(A,B)3,(A,C)5,(A,D)8,(B,E)10,(B,C)6,(C,D)15, (C,E)12,(C,F)9,(D,F)4,(D,G)20,(E,F)18,(F,G)25}; 用克鲁斯卡尔算法求解最小生成树,写出依次得到的各条边。
题目
已知一个图的顶点集V和边集E分别为: V={A,B,C,D,E,F,G}; E={(A,B)3,(A,C)5,(A,D)8,(B,E)10,(B,C)6,(C,D)15, (C,E)12,(C,F)9,(D,F)4,(D,G)20,(E,F)18,(F,G)25}; 用克鲁斯卡尔算法求解最小生成树,写出依次得到的各条边。
相似考题
参考答案和解析
更多“已知一个图的顶点集V和边集E分别为: V={A,B,C,D,E,F,G}; E={(A,B)3,(A,C)5,(A,D)8,(B,E)10,(B,C)6,(C,D)15, (C,E)12,(C,F)9,(D,F)4,(D,G)20,(E,F)18,(F,G)25}; 用克鲁斯卡尔算法求解最小生成树,写出依次得到的各条边。”相关问题
-
第1题:
已知一个图的顶点集V={1,2,3,4,5,6,7};边集E={()3,()5,()8,()10,()6,()15,()12,()9,()4,()20,()18,()25},用克鲁斯卡尔算法得到最小生成树,则在最小生成树中依次得到的各条边为()。
A、(1,2)3,(4,6)4,(1,3)5,(1,4)8,(2,5)10,(4,7)20
B、(1,2)3,(4,6)4,(1,3)5,(2,3)6,(1,4)8,(3,6)9
C、(1,2)3,(1,3)5,(1,4)8,(4,6)4,(2,5)10,(4,7)20
D、(1,2)3,(1,3)5,(1,4)8,(2,5)10,(4,6)4,(4,7)20
参考答案:A
-
第2题:
设任意多面体的顶点数为V,边数为E,面数为F。请根据实例判断并选出正确反映这三者之间关系的公式(65)。
A.V+E=F+2
B.V+F=E+2
C.E×F=V+10
D.E+F=V+10
正确答案:B
解析:任意多面体的顶点数、边数与面数具有确定的关系(欧拉定理),但不要求大家记住这种公式。本题要求考生从给出的4个关系式中舍弃不正确者,选出正确的公式。人们通常用举例的方法排除不正确者,选出正确者。例如,正方体属于六面体,有8个点、12条边、6个面,即V=8,E=12,F=6。对于该例,上述关系式中B与D成立,因此,可以排除选项A与C。再例如,正四面体有4个顶点、6条边、四个面,即V=4,E=6,F=4。对于该例,上述关系式中只有B、C成立,因此,可以排除选项A与D。根据上述两例;排除了选项A、C、D,于是选出了正确答案B。 -
第3题:
已知一个图的顶点集V和边集E分别为:
V={1,2,3,4,5,6,7};
E={(1,2)3,(1,3)5,(1,4)8,(2,5)10,(2,3)6,(3,4)15,(3,5)12,(3,6)9,(4,6)4,(4,7)20,(5,6)18,(6,7)25};
按照普里姆算法从顶点1出发得到最小生成树,试写出在最小生成树中依次得到的各条边。
正确答案:普里姆算法从顶点1出发得到最小生成树为:
(1,2)3, (1,3)5, (1,4)8, (4,6)4, (2,5)10, (4,7)20
-
第4题:
无向图G=(V,E),其中V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是()。A.a,b,e,c,d,f
B.a,c,f,e,b,d
C.a,e,b,c,f,d
D.a,e,d,f,c,b答案:C解析:假设给定图G的初态是所有顶点均未曾访问过。在G中任选一顶点v为初始出发点(源点),则深度优先遍历可定义如下:首先访问出发点v,并将其标记为已访问过:然后依次从v出发搜索v的每个邻接点w。若w未曾访问过,则以w为新的出发点继续进行深度优先遍历,直至图中所有和源点v有路径相通的顶点(亦称为从源点可达的顶点)均已被访问为止。若此时图中仍有未访问的顶点,则另选一个尚未访问的顶点作为新的源点重复上述过程,直至图中所有顶点均已被访问为止。 -
第5题:
当我们在F3中输入公式"=SUM(F1:F2,F4:F6,C3:E3)",如果将它复制到G5中去,那么G5中的内容将是()。
A=SUM(F1:F2,F4:F6,C3:E3)
B=SUM(G1:G2,G4:G6,D3:F3)
C=SUM(G3:G4,G6:G8,D5:F5)
D=SUM(G2:G3,G5:G7,D4:F4)
C
略 -
第6题:
若一个图的顶点集为{a,b,c,d,e,f},边集为{(a,b),(a,c),(b,c),(d,e)},则该图含有()个连通分量。
正确答案:3 -
第7题:
假定一个有向图的顶点集为{a,b,c,d,e,f},边集为{, , < c,f>, < d,c>, < e,b>, < e,d>},则出度为0的顶点个数为(),入度为1的顶点个数为()
正确答案:2;4 -
第8题:
在欧拉公式V-E+F-R=2(B-G)中,F表示()
- A、V顶点数
- B、F面数
- C、E边数
- D、不相连物体个数
正确答案:B -
第9题:
在欧拉公式V-E+F-L=2(B-G)中,V表示()
- A、顶点数
- B、内环数
- C、边数
- D、不相连物体个数
正确答案:A -
第10题:
单选题在欧拉公式V-E+F-R=2(B-G)中,F表示()AV顶点数
BF面数
CE边数
D不相连物体个数
正确答案: B解析: 暂无解析 -
第11题:
单选题当我们在F3中输入公式"=SUM(F1:F2,F4:F6,C3:E3)",如果将它复制到G5中去,那么G5中的内容将是()。A=SUM(F1:F2,F4:F6,C3:E3)
B=SUM(G1:G2,G4:G6,D3:F3)
C=SUM(G3:G4,G6:G8,D5:F5)
D=SUM(G2:G3,G5:G7,D4:F4)
正确答案: A解析: 暂无解析 -
第12题:
填空题若一个图的顶点集为{a,b,c,d,e,f},边集为{(a,b),(a,c),(b,c),(d,e)},则该图含有()个连通分量。正确答案: 3解析: 暂无解析 -
第13题:
设无向图G中的边的集合E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则从顶点a出发进行深度优先遍历可以得到的一种顶点序列为()。
A.aedfcb
B.acfebd
C.aebcfd
D.aedfbc
正确答案:B
-
第14题:
已知图G=(V,E),其中V=(a,b,c,d,e,f),E:{<a,b>,<a,d>,<a,e>,<d,e>,<e, b>,<c,b>,<c,e>,<c,b,<f,e>},则从该图的顶点a出发的深度优先遍历序列是(51),广度优先遍历序列是(52),其深度优先生成树(或森林)是(53),广度优先生成树(或森林)是(54),该图的一个拓扑序列是(55)。
A.abdecf
B.abdcef
C.aebdcf
D.adebfe
正确答案:A
解析:图的深度优先遍历是从图中的某个节点V1出发,访问此节点,然后依次从V1的未被访问的邻接点进行深度优先遍历,直到图中所有和V1有路径相通的节点都被访问到。若此时图中尚有节点未被访问,则选图中的一个未被访问的接点作起点。重复此过程。因此此图的深度优先遍历序列是abcdef。广度优先遍历是先访问结点V1,然后访问V1连接到的所有未被访问的结点V2,V3,,…Vt,再依次访问V2,V3,…,Vt连接到的所有未被访问的结点。如此进行下去,直到访问遍所有结点。冈此,此图的广度优先遍历序列是abdecf。对于连通图,从图的任一顶点出发进行深度优先遍历时,所经过的边与连通图的所有顶点构成的生成树为图的深度优先生成树;从图的任一顶点山发进行广度优先遍历时,所经过的边与连通图的所有顶点构成的生成树为图的广度优先生成树。对于非连通图,图中的每一个连通分量的生成树的集合为生成森林:按深度优先遍历得到的为深度优先生成森林,按广度优先遍历得到的为广度优先生成森林。因此,图G的深度优先生成森林和广度优先生成森林分别为:如果有向图的某个结点序列满足如下条件:若从结点V1到vj有一条路径,则在序列中结点Vi必定在vj之前,则称该序列是一个拓扑序列。任何无环有向图的结点都可以排在一个拓扑序列中。拓扑排序的方法是重复执行下列步骤(1)和(2),直到所有结点均已被输出。1.从图中选择一个入度为0的结点且输出。2.从图中删除此结点及其所有的出边。在可供选择的答案中,C是一个拓扑序列。 -
第15题:
已知关系模式R=(A,B,C,D,E,F,G)满足函数依赖集F=(A→B.B→C,A→E,B→F,(C,D→G),则关系模式R的码是---。
A.(C,D )
B.(B,E)
C.(A,D )
D.(E,F,G)
正确答案:C
解析:设K为关系模式R<u,F>中的属性组,若K→u在F+中,而找不到K的任何一个真子集K’。能使K→U在F+中,则称K为关系模式R的候选码。 -
第16题:
假设某消息中只包含 7 个字符{a,b,c,d,e,f,g},这 7 个字符在消息中出现的次数为{5,24,8,17,34,4,13},利用哈夫曼树(最优二叉树)为该消息中的字符构造符合前缀编码要求的不等长编码。各字符的编码长度分别为(58)。A.a:4,b:2,c:3,d:3,e:2,f:4,g:3
B.a:6,b:2,c:5,d:3,e:1,f:6,g:4
C.a:3,b:3,c:3,d:3,e:3,f:2,g:3
D.a:2,b:6,c:3,d:5,e:6,f:1,g:4答案:A解析: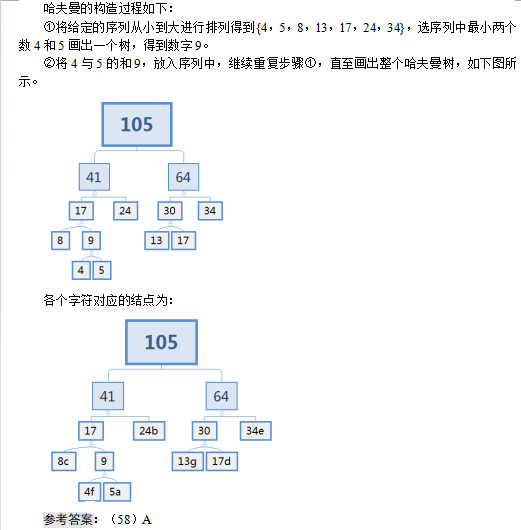
-
第17题:
设连通图G中的边集E={(a,b),(a,e),(a,c),(b,e),(e,d),(d,f),(f,c)},则从顶点a出发可以得到一种深度优先遍历的顶点序列为()
- A、abedfc
- B、acfebd
- C、aebdfc
- D、aedfcb
正确答案:B -
第18题:
假定一个有向图的边集为{,,< c,f>,< d,c>,< e,b>,< e,d>},对该图进行拓扑排序得到的顶点序列为()
正确答案:aebdcf -
第19题:
无向图G=(V,E),其中V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是()。
- A、a,b,e,c,d,f
- B、a,c,f,e,b,d
- C、a,e,b,c,f,d
- D、a,e,d,f,c,b
正确答案:D -
第20题:
故障树T=(A∩B)∪(C∩D∩E)∪(F∩G)有()个最小割集。
- A、7
- B、64
- C、12
- D、3
正确答案:D -
第21题:
在欧拉公式V-E+F-R=2(B-G)中,E表示()
- A、顶点数
- B、内环数
- C、边数
- D、不相连物体个数
正确答案:A -
第22题:
单选题设连通图G中的边集E={(a,b),(a,e),(a,c),(a,e),(b,d),(d,f),(f,c)),则从顶点a出发可以得到一种深度优先遍历的顶点序列为()。Aabedfc
Bacfebd
Cabcedf
Dabcdef
正确答案: A解析: 暂无解析 -
第23题:
单选题无向图G=(V,E),其中:V={a,b,c,d,e,f,E={(a,b),(a,e)(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是( )。Aa,b,e,c,d,f
Ba,c,f,e,b,d
Ca,e,b,c,f,d
Da,e,d,f,c,b
正确答案: C解析: -
第24题:
单选题故障树T=(A∩B)∪(C∩D∩E)∪(F∩G)有()个最小割集。A7
B64
C12
D3
正确答案: B解析: 暂无解析
